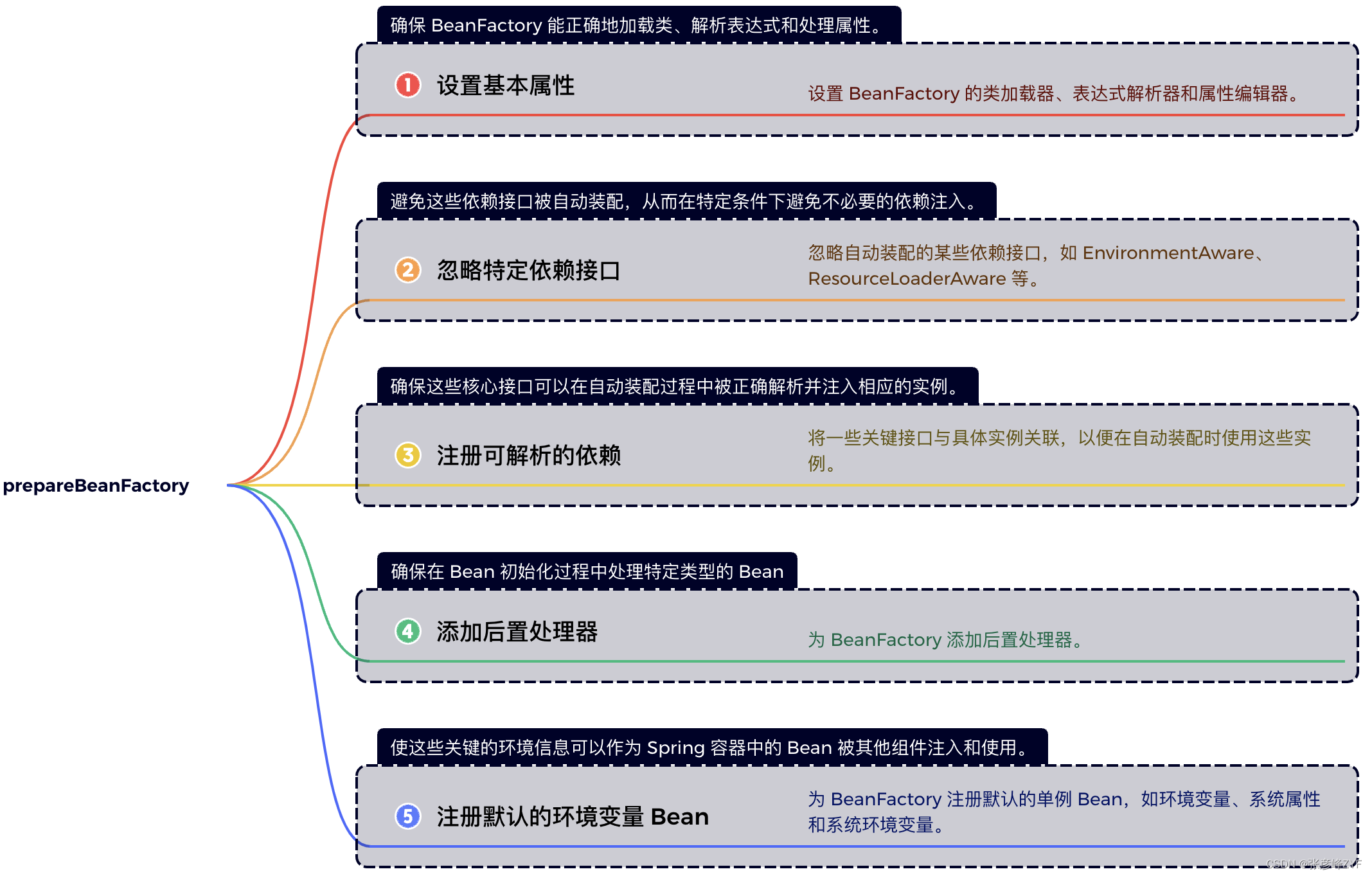
数据结构第一讲:复杂度
- 1.数据结构前言
- 1.1什么是数据结构
- 1.2算法
- 2.算法效率
- 2.1复杂度的概念
- 3.时间复杂度
- 3.1案例1
- 3.2案例2
- 3.3案例3
- 3.4案例4
- 3.5案例5
- 3.6案例6
- 3.7案例7
- 4.空间复杂度
- 4.1案例1
- 4.2案例2
- 5.常见复杂度对比
- 6.轮转数组题目分析
- 6.1优化1
- 6.2优化2
博客简介:
1.该博客是数据结构第一讲,是数据结构初阶的内容,后续会继续输出数据结构高阶的内容
2.数据结构初阶内容全部由C语言来编写
1.数据结构前言
1.1什么是数据结构
将数据比作成一群在草原上的绵羊,绵羊是无序的,如果我们要查找一只叫做“贝蒂”的绵羊,一只一只查找是很耗时耗力的,所以我们要将所有的绵羊组织起来,对他们进行管理,以便于后边的增删查改等操作
像这样的将数据组织、存储的方式就叫做数据结构
1.2算法
算法其实就是解决问题的方法
2.算法效率
首先我们先看一道例题,然后在研究算法效率
案例:轮转数组链接: 力扣链接
我们直接将所写的代码拿上来:
void rotate(int* nums, int numsSize, int k) {
//思路:每一次循环就将一个数字进行轮转
while(k--)
{
int begin = *(nums+numsSize-1);
for(int i = numsSize-1; i>0; i--)
{
*(nums+i) = *(nums+i-1);
}
*nums = begin;
}
}
当我们提交时,我们可以发现:出错了!原因为:

那么为什么会出现超出时间限制这个错误呢,我们往下看:
2.1复杂度的概念
算法的运行需要时间,也需要空间,衡量一个算法的好坏通常是从时间和空间两个方面来看,也就是时间复杂度和空间复杂度
3.时间复杂度
时间复杂度判断总结:
1.只保留高阶项,保留高阶项后要省略掉低阶项
2.高阶项前的系数可以忽略
3.所有的常数项都要被替换成1
4.对于以log形式的函数都可以将底数忽略,写成是logN或者lgN
5.按照最坏的哪一种情况的复杂度作为算法的时间复杂度
下面我们来看具体的分析案例来加深对时间复杂度的理解:
3.1案例1
// 计算Func2的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
// 计算Func2的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N; ++k)
{
//for循环,时间复杂度为2*N
++count;
}
int M = 10;
while (M--)
{
//时间复杂度为M,M为10,那么时间复杂度就是10
++count;
}
printf("%d\n", count);
}
//所以说:该算法的时间复杂度为2*N+10
//表示方法为:O(N)【保留了高阶项2*N,将高阶项前的系数可以忽略】
3.2案例2
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++k)
{
++count;
}
for (int k = 0; k < N; ++k)
{
++count;
}
printf("%d\n", count);
}
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++k)
{
//时间复杂度为M
++count;
}
for (int k = 0; k < N; ++k)
{
//时间复杂度为N
++count;
}
printf("%d\n", count);
}
//所以它的时间复杂度就是M+N
//表示为O(N)即可
3.3案例3
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++k)
{
++count;
}
printf("%d\n", count);
}
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++k)
{
//时间复杂度为100
++count;
}
printf("%d\n", count);
}
//它的时间复杂度为100
//表示为O(1)
3.4案例4
// 计算strchr的时间复杂度?
const char* strchr(const char * str, int character)
{
const char* p_begin = s;
while (*p_begin != character)
{
if (*p_begin == '\0')
return NULL;
p_begin++;
}
return p_begin;
}
// 计算strchr的时间复杂度?
//该函数的作用是查找一个字符在字符串中的位置
const char* strchr(const char * str, int character)
{
const char* p_begin = s;
while (*p_begin != character)
{
if (*p_begin == '\0')
return NULL;
p_begin++;
}
return p_begin;
}
//我们假设字符串中一共有N个字符
//第一种情况(最好的情况):
//查找的第一次就查找到了目标字符,那么这时的时间复杂度就是O(1)
//第二种情况(中间情况):
//目标字符组在字符串的中间位置,那么这时的时间复杂度就是N/2,表示为O(N)
//第三种情况(最坏的情况):
//当目标字符在我们要查找的字符串末尾时,这时的时间复杂度为O(N)
//
//取最坏的情况作为算法最终的时间复杂度,也就是O(N)
3.5案例5
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
// 计算BubbleSort的时间复杂度?
//冒泡排序函数
void BubbleSort(int* a, int n)
{
//这个函数将循环嵌套使用
for (size_t end = n; end > 0; --end)
{
//外层循环的次数为N
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
//外层每循环一次,内层都要交换N-1次
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
//所以说该算法的时间复杂度为一个等差数列进行求和的结果:
//N N-1 ...... 2 1
//结果为N(N+1)/2 , 表示为O(N^2)
3.6案例6
void func5(int n)
{
int cnt = 1;
while (cnt < n)
{
cnt *= 2;
}
}
void func5(int n)
{
int cnt = 1;
while (cnt < n)
{
cnt *= 2;
}
}
//当N取10时,我们来看这个算法是怎么运行的:
//cut 1 2 4 8 16
//ret 2 4 8 16 32
//由于cnt并不是从0开始,一直顺序增加到10的,而是不停的*2做到的,所以此时的时间复杂度并不是O(n)
//当N为10时,循环了4次就做到了,通过我们的分析可以看出,该算法的时间复杂度为O(logN)
3.7案例7
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{
if (0 == N)
return 1;
return Fac(N - 1) * N;
}
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{
if (0 == N)
return 1;
return Fac(N - 1) * N;
}
//这里是计算递归函数的时间复杂度
//不难看出,该函数是从Fac(N-1)递归到了Fac(0)
//也就是从0到N递增运行,时间复杂度为O(N)
我们已经了解到了时间复杂度的计算方法,那么分析一个算法的好坏是否已经是了然于胸了呢,其实不是,判断一个算法的好坏还需要判断它的空间复杂度
当前来说,内存空间是相对而言十分廉价的,我们经常会使用空间来换取时间,那是不是就说明空间可以随意地使用呢,肯定不对!所以我们仍然需要了解空间复杂度的计算方法:
4.空间复杂度
空间复杂度计算针对的仅仅是算法进行过程中临时开辟的内存
4.1案例1
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
for (size_t end = n; end > 0; --end)
{
//size_t end = n 时间复杂度为1
int exchange = 0;
//int exchange = 0 时间复杂度为2(1+1=2)
for (size_t i = 1; i < end; ++i)
{
//size_t i = 1 时间复杂度为3
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
//程序运行时只对三个变量进行了初始化,所以时间复杂度为O(1)
4.2案例2
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}
//每一次函数递归时都要创建一次函数
//所以它的时间复杂度为O(N)
5.常见复杂度对比


6.轮转数组题目分析
我们有了上述的知识之后,再来看我们一开始写的题目:
void rotate(int* nums, int numsSize, int k) {
while (k--)
{
int end = nums[numsSize - 1];
for (int i = numsSize - 1; i > 0; i--)
{
nums[i] = nums[i - 1];
}
nums[0] = end;
}
}
对它进行时间复杂度的分析:
void rotate(int* nums, int numsSize, int k) {
while (k--)
{
//外层循环k次
int end = nums[numsSize - 1];
for (int i = numsSize - 1; i > 0; i--)
{
//外层每循环一次,内层进行N-1次操作
nums[i] = nums[i - 1];
}
nums[0] = end;
}
}
//时间复杂度为O(N^2)
//是一个等差数列
通过复杂度对比表格可以看出,O(n^2)复杂度需要的时间很长,那么我们是否可以将这个算法换成是O(N)或者是O(1)这些算法呢?优化如下:
6.1优化1
思路分析:
申请新数组空间,先将后k个数据放到新数组中,再将剩下的数据挪到新数组中
void rotate(int* nums, int numsSize, int k)
{
int newArr[numsSize];
for (int i = 0; i < numsSize; ++i)
{
newArr[(i + k) % numsSize] = nums[i];
}
for (int i = 0; i < numsSize; ++i)
{
nums[i] = newArr[i];
}
}
时间复杂度分析:
void rotate(int* nums, int numsSize, int k)
{
int newArr[numsSize];
for (int i = 0; i < numsSize; ++i)
{
//时间复杂度为numsSize
newArr[(i + k) % numsSize] = nums[i];
}
for (int i = 0; i < numsSize; ++i)
{
//时间复杂度为numsSize
nums[i] = newArr[i];
}
}
//所以说该算法的时间复杂度为O(N)
//但是它的空间复杂度为O(N),因为创建了一个新的数组,这个数组的大小为numsSize
//这里就是一个空间换取时间的案例
6.2优化2
思路分析:

void reverse(int* nums, int begin, int end)
{
while (begin < end) {
int tmp = nums[begin];
nums[begin] = nums[end];
nums[end] = tmp;
begin++;
end--;
}
}
void rotate(int* nums, int numsSize, int k)
{
k = k % numsSize;
reverse(nums, 0, numsSize - k - 1);
reverse(nums, numsSize - k, numsSize - 1);
reverse(nums, 0, numsSize - 1);
}
时间复杂度分析:
void reverse(int* nums, int begin, int end)
{
while (begin < end) {
int tmp = nums[begin];
nums[begin] = nums[end];
nums[end] = tmp;
begin++;
end--;
}
}
void rotate(int* nums, int numsSize, int k)
{
k = k % numsSize;
reverse(nums, 0, numsSize - k - 1);
//时间复杂度为O(N)
reverse(nums, numsSize - k, numsSize - 1);
//时间复杂度为O(N)
reverse(nums, 0, numsSize - 1);
//时间复杂度为O(N)
}
//所以该函数的时间复杂度为O(N)
//但是它的空间复杂度只有O(1)