离散数学，格与子格，格的性质，格的代数系统定义，格的同态与同构，特殊格

news2024/9/22 9:29:54

目录

1.格与子格 

相互对偶 

2.格的性质 

对偶式 

格的保序性 

3.格的代数系统定义 

格对应的偏序关系就是s的子集之间的包含关系 

该格对应的偏序关系就是整除关系 

子格必然是格 

4.格的同态与同构

格同态，序同态 

 同态是保序的

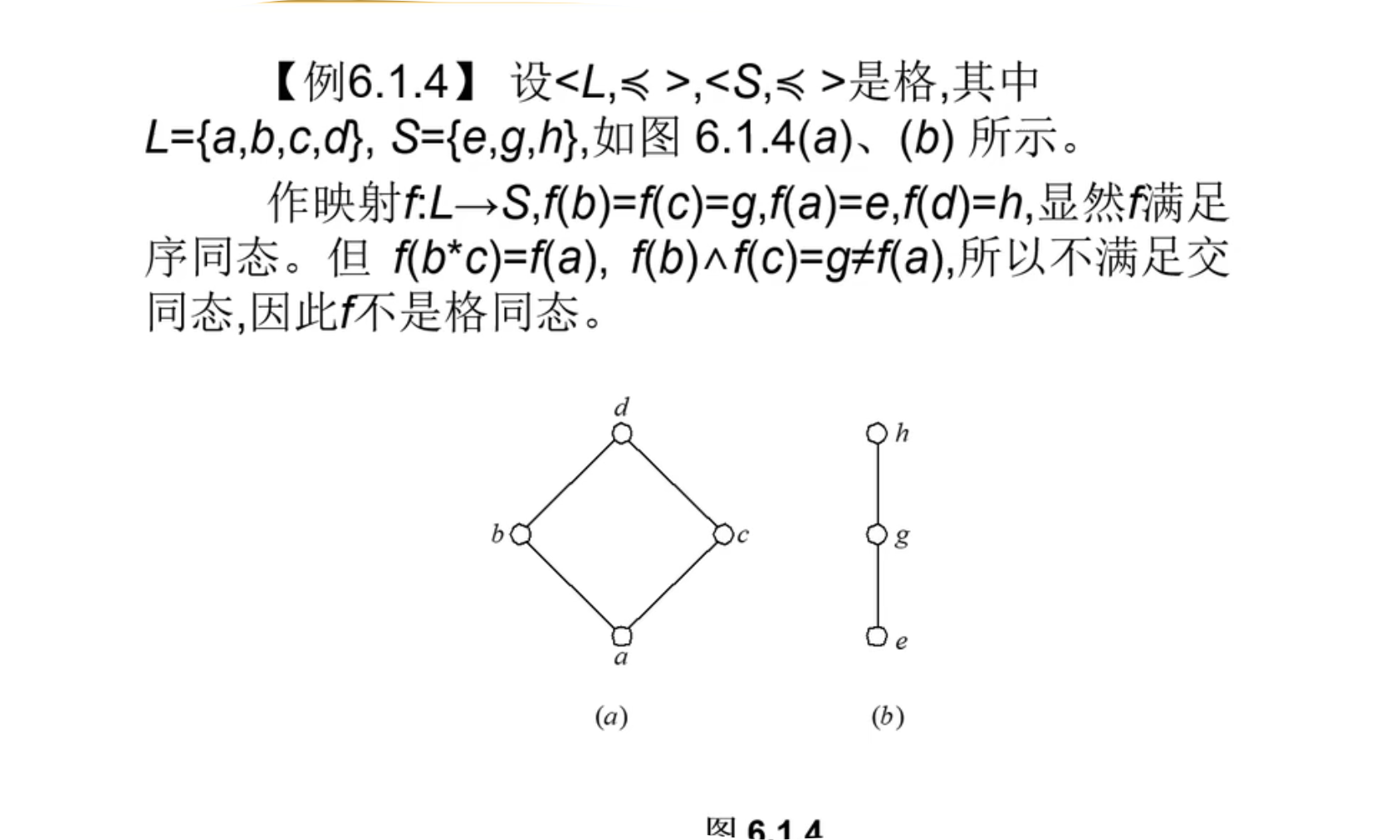
例子 

5.特殊格 

全下（上）界如果存在，则必唯一 

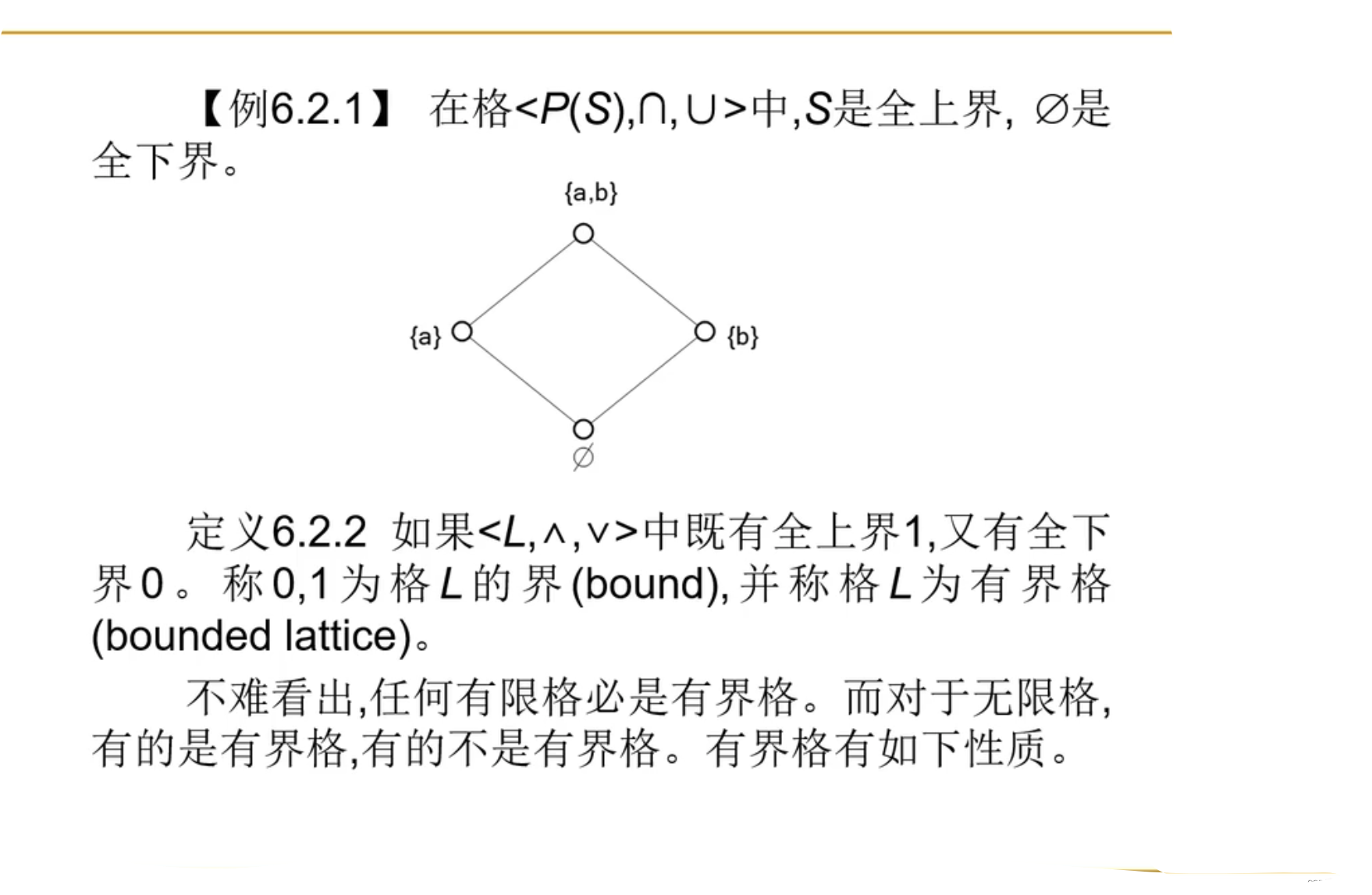
例子 

定理 

1.格与子格 

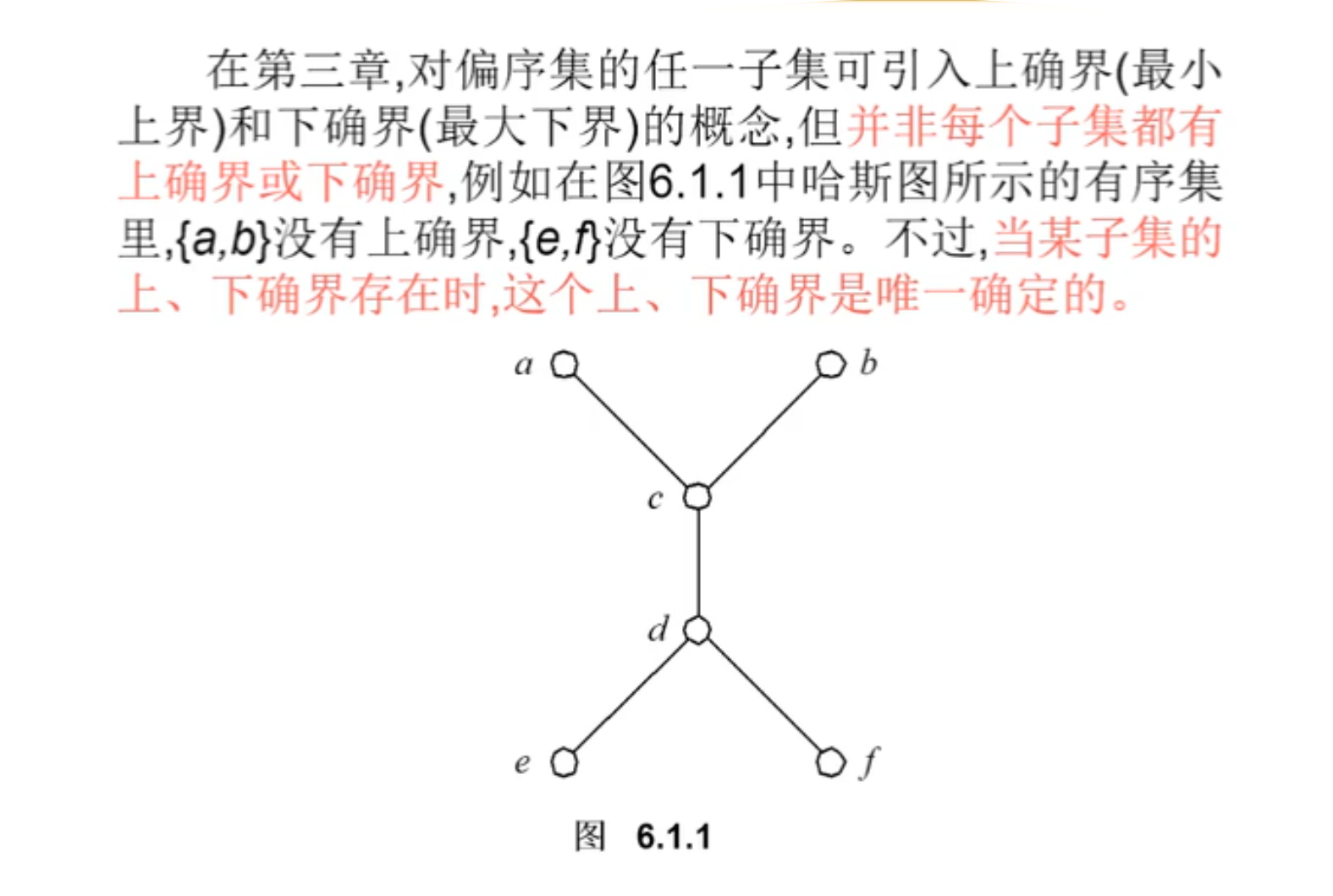
0e371ac0fa364512a29c7053e760abf5.png

29d905a21e184b2b9cdd2bd64f636040.png

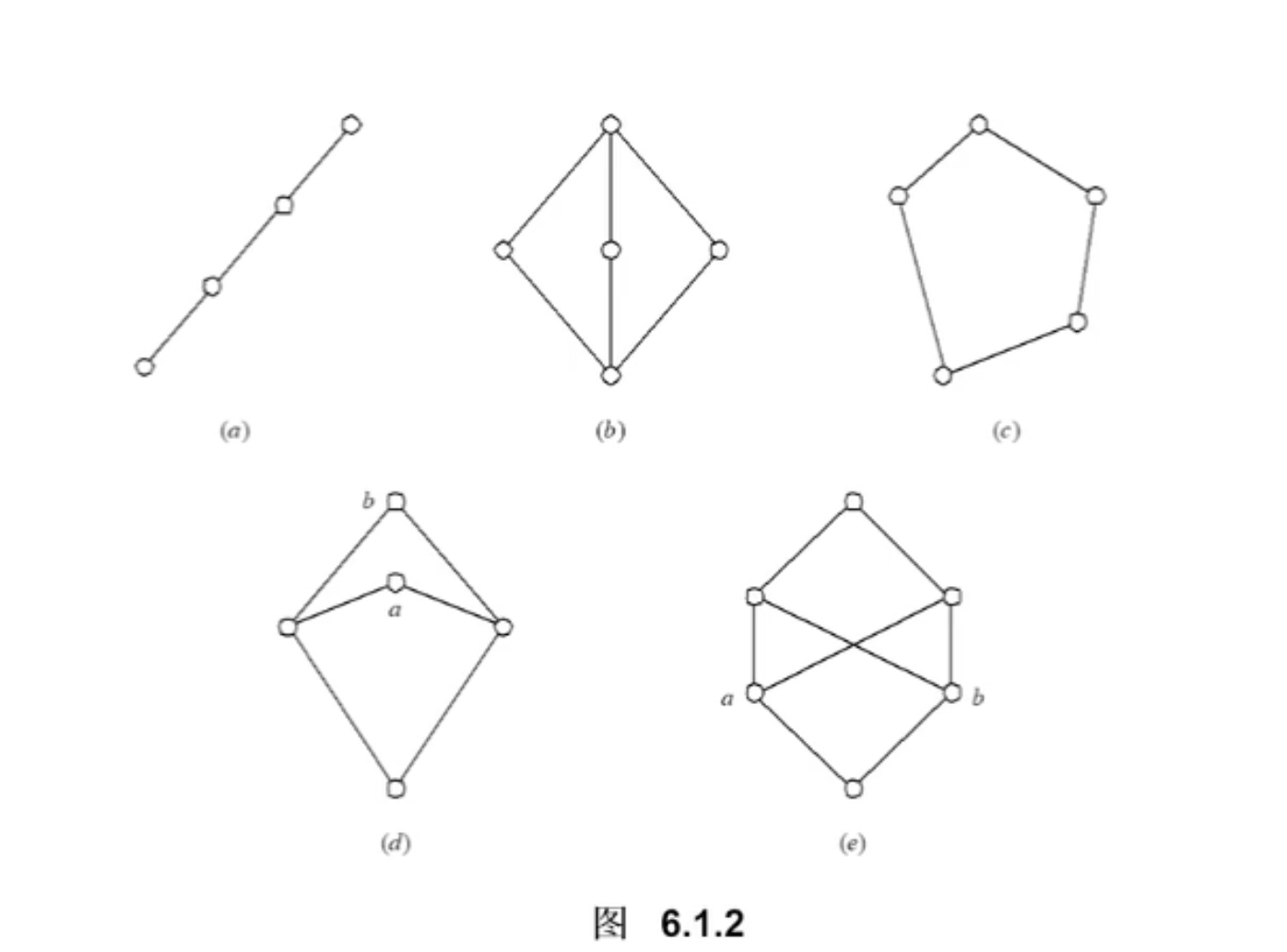
0692f2594d624fd5af4ade41c9c9bccf.png

504dfeb9ac9a40eeb7c4f8db500bec96.png

6794ab1a115f423bab02b4465fe3961f.png

相互对偶 

56667eb55f1541588de4cf0b0e837012.png

2.格的性质 

3c97d590a6fd440f99cd55574585539e.png

对偶式 

d3f3959497574a68aef4081d7137e15c.png

格的保序性 

6d21a2ff35524155a5d9f34fb37a5f56.png

77f2e4435e004e6e89e59acb53467ac4.png

c73666e91dcf44f6adbf20b664d9b8c1.png

8876f28a440444208b188a0b40a70a33.png

dcde7d4b08444dc1a8e2a5269bb2b87d.png

6008c1207cc441878dcfe0f2ca917734.png

100ae63e7cb34f9d8b9d1c5e8c9a1c5b.png

d4798d3da83a49e7a42954bcbda6f01f.png

5413c79d4ae642978c6245a33bfde7cf.png

1b5f3924f6234e9a82578b2ad3b712d4.png

a607a1e577df4707ba9f55ed1d875bba.png

3.格的代数系统定义 

 84450ce51d3a4757abc891ddfbd65178.png

74b4ec2bc78f4a6dbc22661b10d242be.png

d33b2965d2fa4482a905e53b75ea2345.png

05cb09f7ebd548abba453e403ead44fd.png

格对应的偏序关系就是s的子集之间的包含关系 

78be97a543b54637891273887550d253.png

该格对应的偏序关系就是整除关系 

0ed3078f8aeb4082a47c7bd46f9e65f8.png

子格必然是格 

b52119cd07574f29b14a4174f6245b9c.png

252f3a68b7b34ff99df88b9a7fdbbd65.png

4.格的同态与同构

格同态，序同态 

 d07fc05726b7451ba031f4a3b7c374c6.png

 同态是保序的

c7b0d28e9e3c49beb523047d6fabd40a.png

例子 

8217a322e324429b8863a94381c34915.png

a950cd31f8d04191af1451e884b0912d.png

c43591131ee4423ead47311639bf0a22.png

5cdceb12ec3a4e87a1cf30e15d246c24.png

48461a0e742e4078896ed13966f991d8.png

1e440408b29e4f79b30b71c351e2d243.png

944919ec540f4aa9bc2610d2633f9c0c.png

5.特殊格 

42f8a087ab2a4bcc849ebae2f47f4f80.png

全下（上）界如果存在，则必唯一 

4080b340034b48d58eedd7091d8355bb.png

例子 

69a48119a8944af19ea1042651ee4874.png

定理 

865062e237db45cb953e9e9551a43547.png

8f55865c473e40f9aa8598abf22f0ac9.png

 10960e281b9044178c74490e31b9b5c0.png

5521b4c898cb4085975aa123c42d5924.png

f02d6313da89467b96fe55b769732ead.png

3bcf8b8ac31d49bdbd3dde0645633dab.png

65b8f34139354ae3a56474b4be6115ea.png

69231741c5dd444b84b6b92e40a7a128.png

7156eeb285d6483a9877d944e29a65d4.png

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1938765.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

明星应援系统小程序的设计

明星应援系统小程序的设计

管理员账户功能包括：系统首页，个人中心，用户管理，线上应援管理，线下应援管理，应援物品管理，购买订单管理，集资应援管理，集资订单管理，市集订单管理&#xff0…
阅读更多...
CentOS部署MySQL

CentOS部署MySQL

1.配置yum仓库 #更新秘钥 rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysql-2023 #安装MySQL rpm -Uvh http://dev.mysql.com/get/mysql80-community-release-el7-2.noarch.rpm 2.使用yum安装MySQL yum -y install mysql-community-server 3.启动MySQL并配置开机自启…
阅读更多...
PCB系统学习（1）--PCB印制电路板

PCB系统学习（1）--PCB印制电路板

PCB印制电路板 1.1PCB的定义1.2PCB的层叠结构1.2.1PCB单层板1.2.2PCB双层板1.2.3PCB四层板 1.3PCB的通孔，盲孔，埋孔1.4元器件的符号与封装1.5PCB的生产过程 1.1PCB的定义 PCB(PrintedCircuitBoard)，中文即印制电路板，或印刷线路板…
阅读更多...
C语言八皇后问题可视化界面

C语言八皇后问题可视化界面

插件使用easyx 以下是部分代码。需要源码的私信 #include<stdio.h> #include<easyx.h> #define width 1100//设置窗口的宽度和高度 #define height 900 int place[8] { 0 };//皇后位置 int flag[8] { 1,1,1,1,1,1,1,1 };//定义列 int d1[15] { 1,1,1,1,1,1,1,…
阅读更多...
【Node.js基础03】利用http模块创建Web服务

【Node.js基础03】利用http模块创建Web服务

一&#xff1a;使用步骤 1 加载http模块&#xff0c;并创建Web服务程序 2 利用Web服务程序监听request事件&#xff0c;设置响应头和响应体 3 配置端口号并启动Web服务 4 浏览器请求设置的端口号&#xff0c;进行Web服务程序测试 二&#xff1a;简单应用 const http requir…
阅读更多...
HarmonyOS Web组件（二）

HarmonyOS Web组件（二）

1. HarmonyOS Web组件 官方文档 1.1. 混合开发的背景和好处 混合开发&#xff08;Hybrid Development&#xff09;是一种结合原生应用和Web应用的开发模式&#xff0c;旨在同时利用两者的优势。随着移动应用需求的多样化和复杂化&#xff0c;单一的开发方式往往难以满足所有…
阅读更多...
qt 在线安装包下载

qt 在线安装包下载

1.获取在线安装包直接运行安装即可&#xff0c;需要注册或登录会员 如下是官网地址&#xff0c;可以直接注册下线最新版。 官网&#xff1a;https://www.qt.io/ 官网中文&#xff1a;https://www.qt.io/zh-cn/product/qt-for-application-development 下载界面如下&#xff…
阅读更多...
netcat 使用

netcat 使用

GPT-4o (OpenAI) Netcat (通常缩写为nc) 是一个功能强大的网络工具&#xff0c;可以方便地读写网络连接。它被广泛用于漏洞测试、网络调试和数据传输。Netcat 可以作为客户端&#xff0c;也可以作为服务器使用。 以下是一些常见的 Netcat 用法&#xff1a;基础用法 连接到服务…
阅读更多...
Linux系统之部署扫雷小游戏（三）

Linux系统之部署扫雷小游戏（三）

Linux系统之部署扫雷小游戏（三） 一、小游戏介绍1.1 小游戏简介1.2 项目预览二、本次实践介绍2.1 本地环境规划2.2 本次实践介绍三、检查本地环境3.1 检查系统版本3.2 检查系统内核版本3.3 检查软件源四、安装Apache24.1 安装Apache2软件4.2 启动apache2服务4.3 查看apache2服…
阅读更多...
卷积神经网络学习问题总结

卷积神经网络学习问题总结

问题一&#xff1a; 深度学习中的损失函数和应用场景 回归任务&#xff1a; 均方误差函数&#xff08;MSE&#xff09;适用于回归任务&#xff0c;如预测房价、预测股票价格等。 import torch.nn as nn loss_fn nn.MSELoss() 分类任务&#xff1a; 交叉熵损失函数&…
阅读更多...
【C语言已解决】“Segmentation Fault“

【C语言已解决】“Segmentation Fault“

&#x1f3ac; 鸽芷咕&#xff1a;个人主页 &#x1f525; 个人专栏: 《C干货基地》《粉丝福利》 ⛺️生活的理想&#xff0c;就是为了理想的生活! 引言 在编程过程中&#xff0c;遇到 “Segmentation Fault” 报错可能会让你感到沮丧。这个错误提示通常意味着你的程序尝试访问…
阅读更多...
【IEEE出版】第四届能源工程与电力系统国际学术会议（EEPS 2024）

【IEEE出版】第四届能源工程与电力系统国际学术会议（EEPS 2024）

第四届能源工程与电力系统国际学术会议&#xff08;EEPS 2024&#xff09; 2024 4th International Conference on Energy Engineering and Power Systems 重要信息 大会官网&#xff1a;www.iceeps.com 大会时间&#xff1a;2024年8月9-11日 大会…
阅读更多...
物联网在养殖业领域的应用——案例分析

物联网在养殖业领域的应用——案例分析

作者主页: 知孤云出岫 目录 作者主页:物联网在养殖业领域的应用——案例分析背景技术架构硬件设置连接多种传感器到微控制器 代码实现1. Arduino代码&#xff1a;采集多种传感器数据并上传到Thingspeak2. Python代码&#xff1a;从Thingspeak获取数据并进行综合分析和可视化 …
阅读更多...
提升教育质量：智慧校园教师进修助力

提升教育质量：智慧校园教师进修助力

在智慧校园整体解决方案中&#xff0c;教职工管理系统的教师进修功能具有重要作用。它不仅是教师专业成长的催化剂&#xff0c;更是学校教育质量飞跃的加速器。通过智慧化、人性化的管理流程&#xff0c;这一功能赋能教师&#xff0c;让他们能够轻松获取多元化的进修机会&#…
阅读更多...
搭建环境监测

搭建环境监测

原文&#xff1a;https://blog.c12th.cn/archives/30.html 环境监测 测试&#xff1a;笔记本原装操作系统&#xff1a;Windows 10 家庭中文版 资源分享链接&#xff1a;提取码&#xff1a;zjv2 卸载SQL步骤&#xff1a; https://blog.csdn.net/qq1623803207/article/details/7…
阅读更多...
【Vue3】计算属性

【Vue3】计算属性

【Vue3】计算属性 背景简介开发环境开发步骤及源码 背景 随着年龄的增长&#xff0c;很多曾经烂熟于心的技术原理已被岁月摩擦得愈发模糊起来&#xff0c;技术出身的人总是很难放下一些执念&#xff0c;遂将这些知识整理成文&#xff0c;以纪念曾经努力学习奋斗的日子。本文内…
阅读更多...
小白快速入门量化交易的自学路径

小白快速入门量化交易的自学路径

今年已然过去一半了&#xff0c;年初立的flag都实现了吗&#xff1f; 据我多年来的观察&#xff0c;很多小白萌新开始学习量化&#xff0c;特别是年初的时候立下“宏图大志”&#xff0c;但有相当一部分最终没能"上岸"&#xff0c;从入门到放弃&#xff0c;从然后到没…
阅读更多...
Amesim中界面显示字体设置

Amesim中界面显示字体设置

对于大屏使用Amesim软件&#xff0c;系统默认的字体可能会很小不方便进行查看使用。在Amesim中我们可以通过设置显示字体的大小来解决此问题。 For large screens, the default font of the system may be small and inconvenient to view. In Amesim we can solve this probl…
阅读更多...
24暑假算法刷题 | Day18 | LeetCode 530. 二叉搜索树的最小绝对差，501. 二叉搜索树中的众数，236. 二叉树的最近公共祖先

24暑假算法刷题 | Day18 | LeetCode 530. 二叉搜索树的最小绝对差，501. 二叉搜索树中的众数，236. 二叉树的最近公共祖先

目录 530. 二叉搜索树的最小绝对差题目描述题解 501. 二叉搜索树中的众数题目描述题解 236. 二叉树的最近公共祖先题目描述题解 530. 二叉搜索树的最小绝对差 点此跳转题目链接 题目描述 给你一个二叉搜索树的根节点 root &#xff0c;返回 树中任意两不同节点值之间的最小差…
阅读更多...
Flink调优详解：案例解析（第42天）

Flink调优详解：案例解析（第42天）

系列文章目录 一、Flink-任务参数配置 二、Flink-SQL调优 三、阿里云Flink调优 文章目录 系列文章目录前言一、Flink-任务参数配置1.1 运行时参数1.2 优化器参数1.3 表参数 二、Flink-SQL调优2.1 mini-batch聚合2.2 两阶段聚合2.3 分桶2.4 filter去重&#xff08;了解&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023