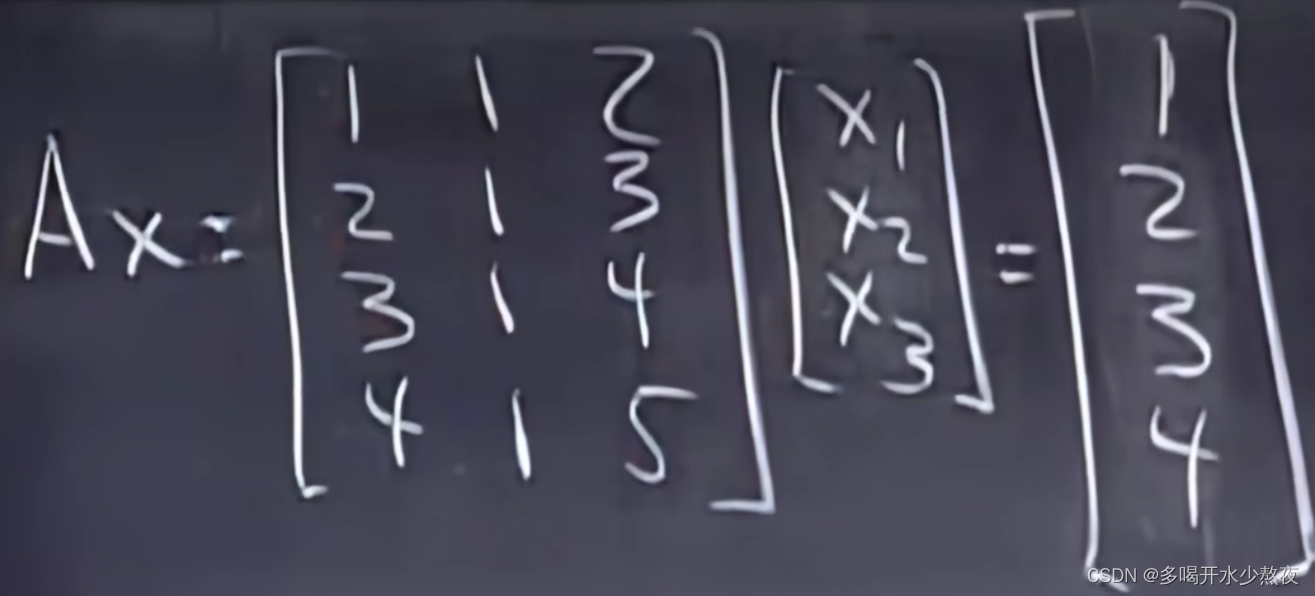目录
一、基础认识
1. 介绍
2. 认识 “ 维度 ”
(1)数组和Series
(2)DataFrame 表
(3)图像
3. 降维思想
4. 降维步骤
二、降维算法(PCA)
1. PCA实现
(1)PCA参数
(2)PCA属性
(3)PCA接口
2. PCA中的SVD
3. 训练流程
4. 补充
三、学习中产生的疑问,及文心一言回答
1. PCA中的components_属性
一、基础认识
1. 介绍
与特征选择类似,我们可以 用不同的特征提取技术来减少数据集的特征数量。特征选择和特征提取的区别在于,当我们用诸如 逆序选择之类的特征选择算法 时,数据集的原始特征 保持不变,而当我们用 特征提取 方法时,会将数据变换 或投影到 新特征空间。在降维的背景下,我们可以 把特征提取理解为 数据压缩的一种方法,其目的是 保持大部分的相关信息。
在实际应用中,特征提取 不仅可以优化存储空间 或 机器学习算法 的计算效率,而且还可以 通过减少 维数 提高预测性能,尤其是当我们 处理非正则化 模型的时候。
2. 认识 “ 维度 ”
(1)数组和Series
对于 数组 和 Series来说,维度就是功能shape返回的结果,shape中 返回了 几个数字,就是几维。

(2)DataFrame 表
数组中的 每一张表,都可以是 一个特征矩阵 或 一个 DataFrame,表中 行是 样本,列 是特征。针对每一张表,维度 指的是 样本的数量 或 特征的数量,一般无特别说明,指的都是特征的数量。除了索引之外,一个特征是一维,两个特征是二维,n 个特征是 n维。

(3)图像
对图像 来说,维度就是图像中特征向量的数量。特征向量可以理解为是 坐标轴,一个特征向量定义一条直线,是 一维,两个相互垂直的特征向量定义一个 平面,即一个直角坐标系,就是二维,三个相互垂直的特征向量定义一个空间,即一个立体直角坐标系,就是三维。三个以上的特征向量相互垂直,定义人眼无法看见,也无法想象的高维空间。

降维算法中的 “ 降维 ”,指的是 降低 特征矩阵中 特征的 数量。
3. 降维思想
在降维过程中,我们会 减少特征的 数量,这意味着 删除数据,数据量 变少则 表示模型 可以获取的 信息会变少,模型的表现 可能会因此 受影响。同时,在高维数据中,必然有一些无效信息(比如噪音),或者一些重复信息(比如一些特征可能会线性相关)。
我们希望能够找出一种办法来帮助我们衡量特征上所带的信息量,让我们在降维的过程中,能够即减少特征的数量,又保留大部分有效信息
将那些带有重复信息的特征合并,并删除那些带无效信息的特征,逐浙创造出能够代表原特征矩阵大部分信息的,特征更少的,新特征矩阵。
现在有一组简单的数据,有特征 x1 和 x2,三个样本数据的坐标点分别为(1,1),(2,2),(3,3)。我们 可以让 x1 和 x2 分别作为 两个特征向量,很轻松地用一个 二维平面来描述 这组数据。这组数据 现在 每个特征的 均值都为 2,特征的数据一模一样,因此 方差也都为1,数据的 方差总和 是 2。
现在我们的 目标 是:只用 一个特征向量 来描述这组数据,即将 二维数据降为 一维数据,并且尽可能地 保留信息量,即 让数据的 总方差 尽量靠近 2。
据图所知,我们根据 信息含量的排序,取信息含量 最大的 一个特征,可以将 x2* 删除,同时也删除图中的 x2* 特征向量,剩下的 x1* 就代表了曾经需要 两个特征来代表的 三个样本点。 通过 旋转原有 特征向量组成的 坐标轴 来找到 新特征向量 和 新坐标平面,我们 将三个样本点 的信息 压缩到了 一条直线上,实现了 二维变一维,并且尽量保留原始数据的信息。—个成功的降维,就实现了。
4. 降维步骤
(1)输入原数据,结构为(m,n)。找出原本的n个特征向量构成的n维空间V。
(2)决定降维后的特征数量:k。
(3)通过某种变化,找出n个新的特征向量,以及它们构成的新n维空间V。
(4)找出原始数据在新特征空间V中的n个新特征向量上对应的值,即“将数据映射到新空间中”。
(5)选取前k个信息量最大的特征,删掉没有被选中的特征,成功将n维空间V降为k维。
在步骤(3)当中,我们用来找出 n 个 新特征向量,让 数据 能够 被压缩到 少数特征 上并且 总信息量 不损失太多的技术 就是 矩阵分解,PCA 和 SVD 是 两种不同的 降维算法,但他们都 遵从上面的 过程来 实现降维,只是 两种算法中 矩阵分解的方法 不同,信息量的衡 量 指标不同。
二、降维算法(PCA)
涉及sklearn库:decomposition

1. PCA实现
class sklearn.decomposition.PCA (n_components=None, copy=True, whiten=False, svdl solver=auto',tol=0.0,iterated_power=‘auto’,random_state=None)
(1)PCA参数



(2)PCA属性

(3)PCA接口

2. PCA中的SVD
对于任意(m, n)的输入矩阵 A,SVD 分解 结果为:

分解结果中 U 为 左奇异矩阵,S 为 奇异值矩阵,除 主对角线上的元素外全为 0,主对角线上的每个元素都称为 奇异值,V 为右 奇异矩阵。
右奇异矩阵V有着如下性质:

k 就是 n_components,即 我们降维后希望得到的 维度。若 X 为(m,n)的 特征矩阵,V 就是结构为(n,n)的矩阵,取这个矩阵的前 k 行(进行切片),即将 V 转换为结构为(k,n)的矩阵,与原特征矩阵 X 相乘,即可得到降维后的 特征矩阵 Xdr。
这是说,奇异值分解 可以 不计算 协方差矩阵 等 结构复杂计算冗长的 矩阵,就直接 求出 新特征空间 和 降维后 的 特征矩阵。所以 SVD 在矩阵分解中的 过程比 PCA 简单快速。
3. 训练流程

通过 SVD 和 PCA 的合作,sklearn 实现了一种计算更快 更简单,但效果却很好的 “ 合作降维 ”。
4. 补充
(1)在新的特征矩阵生成之前,我们无法知晓 PCA 都建立了怎样的 新特征向量,新特征矩阵生成之后也 不具有可读性,我们 无法判断 新特征矩阵的特征 是 从原数据中的 什么特征组合 而来,新特征带有 原始数据的信息,却 已经不是 原数据上代表着 的含义了。以 PCA 为代表的 降维算法因此是 特征创造 (feature creation,或 feature construction) 的一种。
(2)inverse_transform 并没有实现数据的 完全逆转。这是因为,在降维的时候,部分信息 已经被舍奔了,Xdr 中往往不会包含原数据 100% 的信息,所以在 逆转的时候,即 便维度升高,原数据中 已经被舍弃的信息也不可能再回来了。所以,降维 不是完全 可逆的。( PCA 可以 对噪音进行过滤)
三、学习中产生的疑问,及文心一言回答
1. PCA中的components_属性