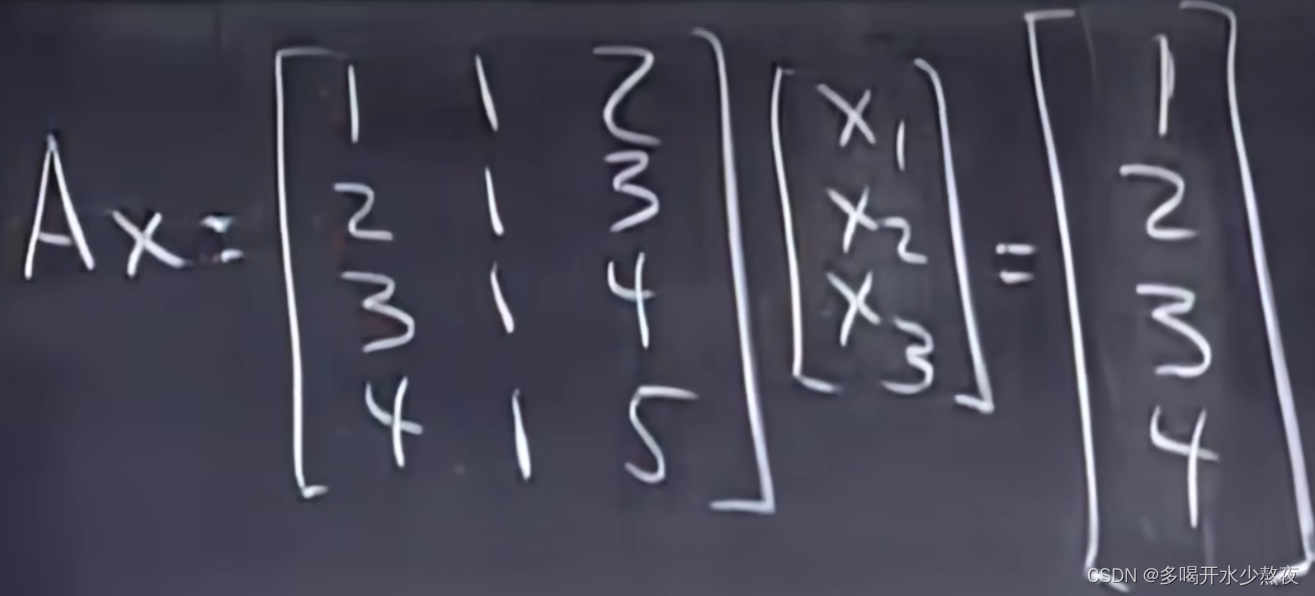要得出平均值定理，我们首先需要以下结果。

罗尔定理

设函数 $f$ 满足以下三个假设：

1. $f$ 在闭区间 $[a,b]$ 上连续。
2. $f$ 在开区间 $(a,b)$ 上可导。
3. $f(a)=f(b)$

则在开区间 $(a,b)$ 内存在一个数 $c$，使得 $f^{\prime }(c)=0$。

在给出证明之前，让我们先看一些满足这三个假设的典型函数的图形。图显示了四个此类函数的图形。在每种情况下，图上似乎至少有一个点 ((c, f©))，该点处的切线是水平的，因此 ( f’© = 0 )。因此，罗尔定理是合理的。

例子 1 让我们将罗尔定理应用于一个运动物体的位置函数 $s=f(t)$。如果物体在两个不同的时刻 $t=a$ 和 $t=b$ 处于相同的位置，则 $f(a)=f(b)$。罗尔定理表明，在 $a$ 和 $b$ 之间的某个时刻 $t=c$，存在 $f^{\prime }(c)=0$；也就是说，速度为0。（当一个球被直接向上抛时，你可以看到这一点是成立的。）

例子 2 证明方程 (x^3 + x - 1 = 0) 恰好有一个实数根。

解答

首先我们使用介值定理（Intermediate Value Theorem）来证明存在一个根。令 $f(x)=x^3+x-1$。那么 $f(0)=-1<0$ 和 $f(1)=1>0$。因为 $f$ 是一个多项式函数，它在整个区间上是连续的，因此根据介值定理，在 $[0,1]$ 区间内存在一个数 $c$，使得 $f(c)=0$。因此，给定的方程存在一个根。

为了证明该方程没有其他实数根，我们使用罗尔定理（Rolle’s Theorem）并通过反证法来进行论证。假设它有两个根 $a$ 和 $b$。那么 $f(a)=0$ 和 $f(b)=0$，并且由于 $f$ 是一个多项式，它在 $(a,b)$ 上可导并在 $[a,b]$ 上连续。因此，根据罗尔定理，在 $(a,b)$ 内存在一个数 $c$，使得 $f^{\prime }(c)=0$。

但是，对于微分方程
$$f^{\prime }(x)=3x^2+1$$
因为 $x^2\ge 0$，所以 $f^{\prime }(x)$ 永远不可能等于0。这导致了矛盾。因此，方程不能有两个实数根。

我们主要使用罗尔定理来证明以下重要定理，这一定理最初是由另一位法国数学家Joseph-Louis Lagrange提出的。

平均值定理

设 $f$ 是满足以下假设的函数：

1. $f$ 在闭区间 $[a,b]$ 上连续。
2. $f$ 在开区间 $(a,b)$ 上可导。
   那么在 $(a,b)$ 中存在一个数 $c$，使得
   $$f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}$$
   或者等价地，
   $$f(b)-f(a)=f^{\prime }(c)(b-a)$$

在证明这个定理之前，我们可以通过几何解释来看它是合理的（如图所示）。

证明

我们将罗尔定理应用于一个新函数 $h$，该函数定义为 $f$ 和割线 $AB$ 所对应的函数之差。使用直线的点斜式方程，我们可以看到直线 $AB$ 的方程可以写成

$$y-f(a)=\frac{f(b)-f(a)}{b-a}(x-a)$$

或者写成

$$y=f(a)+\frac{f(b)-f(a)}{b-a}(x-a)$$

因此，如图所示，

$$h(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)$$

首先我们必须验证 $h$ 满足罗尔定理的三个假设。

1. 函数 $h$ 在 $[a,b]$ 上连续，因为它是 $f$ 和一个一阶多项式的和，两者都是连续的。
2. 函数 $h$ 在 $(a,b)$ 上可导，因为 $f$ 和这个一阶多项式都是可导的。实际上，我们可以直接计算 $h^{\prime }(x)$：

$$h^{\prime }(x)=f^{\prime }(x)-\frac{f(b)-f(a)}{b-a}$$

（注意 $f(a)$ 和 $\frac{f(b)-f(a)}{b-a}$ 是常数。）

$$\begin{array}{rl}h(a)& =f(a)-f(a)-\frac{f(b)-f(a)}{b-a}(a-a)=0\\ h(b)& =f(b)-f(a)-\frac{f(b)-f(a)}{b-a}(b-a)\\ & =f(b)-f(a)-[f(b)-f(a)]=0\end{array}$$

因此 $h(a)=h(b)$。

因为 $h$ 满足罗尔定理的假设，该定理说明在 $(a,b)$ 中存在一个数 $c$，使得 $h^{\prime }(c)=0$。因此，

$$0=h^{\prime }(c)=f^{\prime }(c)-\frac{f(b)-f(a)}{b-a}$$

于是

$$f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}$$

例子 3 为了用一个具体的函数说明平均值定理，让我们考虑 $f(x)=x^3-x$，其中 $a=0$，$b=2$。由于 $f$ 是一个多项式，它在所有 $x$ 上都是连续和可导的，因此它在 $[0,2]$ 上肯定是连续的，并且在 $(0,2)$ 上是可导的。因此，根据平均值定理，在 $(0,2)$ 中存在一个数 $c$，使得

$$f(2)-f(0)=f^{\prime }(c)(2-0)$$

现在 $f(2)=6$，$f(0)=0$，并且 $f^{\prime }(x)=3x^2-1$，因此这个方程变成

$$6=(3c^2-1)2=6c^2-2$$

这给出了 $c^2=\frac{4}{3}$，即 $c=\pm \frac{2}{\sqrt{3}}$。但 $c$ 必须在 $(0,2)$ 中，因此 $c=\frac{2}{\sqrt{3}}$。图中展示了这个计算：在这个 $c$ 值处的切线平行于割线 $OB$。

例子 4 如果一个物体沿直线运动，其位置函数为 $s=f(t)$，那么在 $t=a$ 和 $t=b$ 之间的平均速度为

$$\frac{f(b)-f(a)}{b-a}$$

并且在 $t=c$ 时的速度为 $f^{\prime }(c)$。因此，平均值定理告诉我们，在 $a$ 和 $b$ 之间的某个时刻 $t=c$，瞬时速度 $f^{\prime }(c)$ 等于该平均速度。例如，如果一辆车在2小时内行驶了180公里，那么车速计必须至少有一次显示90公里/小时。

一般来说，平均值定理可以解释为在某个时刻，瞬时变化率等于区间上的平均变化率。

平均值定理的主要意义在于它使我们能够通过导数的信息来获得函数的信息。下一个例子提供了这个原理的一个实例。

例子 5 假设 $f(0)=-3$ 且 $f^{\prime }(x)\le 5$ 对于所有 $x$ 都成立。那么 $f(2)$ 最大可能是多少？

解答

我们知道 $f$ 在所有地方都是可导的（因此也是连续的）。特别地，我们可以在区间 $[0,2]$ 上应用平均值定理。存在一个数 $c$，使得

$$f(2)-f(0)=f^{\prime }(c)(2-0)$$

所以

$$f(2)=f(0)+2f^{\prime }(c)=-3+2f^{\prime }(c)$$

我们已知 $f^{\prime }(x)\le 5$ 对于所有 $x$ 都成立，所以特别地我们知道 $f^{\prime }(c)\le 5$。将这个不等式的两边乘以$2$，我们得到 $2f^{\prime }(c)\le 10$，所以

$$f(2)=-3+2f^{\prime }(c)\le -3+10=7$$

因此 $f(2)$ 最大可能的值是 $7$。

定理

如果 $f^{\prime }(x)=0$ 对所有在区间 $(a,b)$ 内的 $x$ 都成立，那么 $f$ 在 $(a,b)$ 上是常数。

证明 设 $x_1$ 和 $x_2$ 是 $(a,b)$ 中的任意两个数，且 $x_1<x_2$。由于 $f$ 在 $(a,b)$ 上可导，因此它在 $(x_1,x_2)$ 上也必定可导，并且在 $[x_1,x_2]$ 上连续。应用均值定理于 $f$ 在区间 $[x_1,x_2]$ 上，我们可以得到一个数 $c$ 满足 $x_1<c<x_2$，且

$$f(x_2)-f(x_1)=f^{\prime }(c)(x_2-x_1)$$

由于 $f^{\prime }(x)=0$ 对所有 $x$ 成立，我们有 $f^{\prime }(c)=0$，因此公式变为

$$f(x_2)-f(x_1)=0\text{或}f(x_2)=f(x_1)$$

因此， $f$ 在 $(a,b)$ 中的任意两个数 $x_1$ 和 $x_2$ 上具有相同的值。这意味着 $f$ 在 $(a,b)$ 上是常数。

推论

如果 $f^{\prime }(x)=g^{\prime }(x)$ 对在区间 $(a,b)$ 内的所有 $x$ 成立，那么 $f-g$ 在 $(a,b)$ 上是常数；即，$f(x)=g(x)+c$，其中 $c$ 是一个常数。

证明

令 $F(x)=f(x)-g(x)$。则

$$F^{\prime }(x)=f^{\prime }(x)-g^{\prime }(x)=0$$

对在 $(a,b)$ 内的所有 $x$ 成立。因此，根据定理，$F$ 是常数；即，$f-g$ 是常数。