文章目录
- 1、简介
- 2、torch.cat
- 3、torch.stack
- 4、数学过程
- 4.1、维度拼接
- 4.1.1、二维张量
- 4.1.2、三维张量
- 4.1.3、具体实例
- 4.2、维度叠加
- 4.2.1、0维叠加
- 4.2.2、1维叠加
- 4.2.3、2维叠加(非常重要⭐)
🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法,初步涉猎人工智能和前端开发。
🦅个人主页:@逐梦苍穹
📕所属专栏:人工智能
🌻gitee地址:xzl的人工智能代码仓库
✈ 您的一键三连,是我创作的最大动力🌹
1、简介
张量拼接是将两个或多个张量沿指定维度连接起来的操作,这是在神经网络搭建过程中是非常常用的方法。
在深度学习和数据处理的过程中,经常需要将多个张量拼接成一个更大的张量。
张量拼接:
- 定义:张量拼接是将两个或多个张量沿着指定的维度连接起来,形成一个新的张量。
- 应用:常用于数据预处理、特征组合、模型输出处理等场景。
- 要求:被拼接的张量在非拼接维度上的形状必须一致。
2、torch.cat
torch.cat 函数可以将两个张量根据指定的维度拼接起来。
# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/17 1:28
import torch
def test():
data1 = torch.randint(0, 10, [3, 5, 4])
data2 = torch.randint(0, 10, [3, 5, 4])
print(data1)
print(data2)
print('-' * 50)
# 1. 按0维度拼接
new_data = torch.cat([data1, data2], dim=0)
print(new_data.shape)
print('-' * 50)
# 2. 按1维度拼接
new_data = torch.cat([data1, data2], dim=1)
print(new_data.shape)
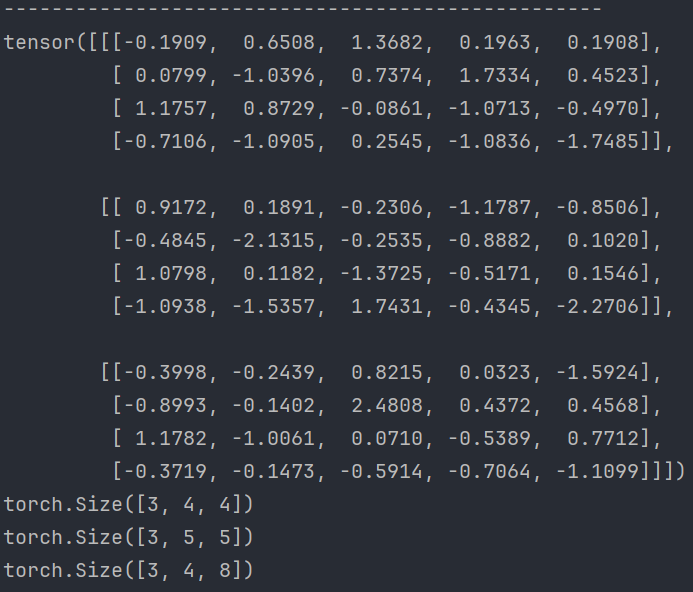
# 3. 按2维度拼接
new_data = torch.cat([data1, data2], dim=2)
print(new_data)
if __name__ == '__main__':
test()
运行结果:
E:\anaconda3\python.exe D:\Python\AI\PyTorch\11-张量拼接.py
tensor([[[0, 7, 4, 8],
[7, 7, 9, 6],
[2, 6, 8, 2],
[7, 1, 0, 3],
[8, 0, 2, 4]],
[[0, 1, 0, 9],
[5, 1, 9, 8],
[7, 8, 8, 5],
[0, 6, 0, 0],
[0, 8, 9, 2]],
[[4, 2, 2, 3],
[7, 9, 0, 9],
[2, 7, 8, 8],
[6, 9, 8, 5],
[3, 6, 9, 8]]])
tensor([[[7, 2, 3, 8],
[3, 1, 6, 3],
[4, 0, 2, 8],
[6, 9, 8, 9],
[1, 1, 5, 2]],
[[4, 0, 2, 2],
[0, 0, 7, 4],
[9, 3, 9, 2],
[1, 5, 9, 5],
[7, 5, 7, 6]],
[[1, 8, 3, 9],
[4, 2, 6, 4],
[6, 6, 6, 9],
[2, 5, 0, 5],
[9, 0, 1, 2]]])
--------------------------------------------------
torch.Size([6, 5, 4])
--------------------------------------------------
torch.Size([3, 10, 4])
tensor([[[0, 7, 4, 8, 7, 2, 3, 8],
[7, 7, 9, 6, 3, 1, 6, 3],
[2, 6, 8, 2, 4, 0, 2, 8],
[7, 1, 0, 3, 6, 9, 8, 9],
[8, 0, 2, 4, 1, 1, 5, 2]],
[[0, 1, 0, 9, 4, 0, 2, 2],
[5, 1, 9, 8, 0, 0, 7, 4],
[7, 8, 8, 5, 9, 3, 9, 2],
[0, 6, 0, 0, 1, 5, 9, 5],
[0, 8, 9, 2, 7, 5, 7, 6]],
[[4, 2, 2, 3, 1, 8, 3, 9],
[7, 9, 0, 9, 4, 2, 6, 4],
[2, 7, 8, 8, 6, 6, 6, 9],
[6, 9, 8, 5, 2, 5, 0, 5],
[3, 6, 9, 8, 9, 0, 1, 2]]])
Process finished with exit code 0
3、torch.stack
torch.stack 函数可以将两个张量根据指定的维度叠加起来.
def test2():
data1 = torch.randint(0, 10, [2, 3])
data2 = torch.randint(0, 10, [2, 3])
print(data1)
print(data2)
new_data = torch.stack([data1, data2], dim=0)
print(new_data)
print(new_data.shape)
new_data = torch.stack([data1, data2], dim=1)
print(new_data)
print(new_data.shape)
new_data = torch.stack([data1, data2], dim=2)
print(new_data)
print(new_data.shape)
输出:
E:\anaconda3\python.exe D:\Python\AI\PyTorch\11-张量拼接.py
tensor([[4, 2, 9],
[5, 2, 2]])
tensor([[8, 4, 7],
[4, 7, 3]])
tensor([[[4, 2, 9],
[5, 2, 2]],
[[8, 4, 7],
[4, 7, 3]]])
torch.Size([2, 2, 3])
tensor([[[4, 2, 9],
[8, 4, 7]],
[[5, 2, 2],
[4, 7, 3]]])
torch.Size([2, 2, 3])
tensor([[[4, 8],
[2, 4],
[9, 7]],
[[5, 4],
[2, 7],
[2, 3]]])
torch.Size([2, 3, 2])
Process finished with exit code 0
4、数学过程
维度拼接和维度叠加的本质区别:
维度拼接不改变矩阵维度
维度叠加会增加矩阵维度
4.1、维度拼接
先说结论:
- 维度拼接的本质,就是沿着轴方向进行拼接
- 轴的编号定义,由外往内依次为0,1,2,…,n
4.1.1、二维张量
先用简单的二维张量引入
假设有两个二维张量 A 和 B:
[
A
=
(
1
2
3
4
)
]
[ A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} ]
[A=(1324)]
[
B
=
(
5
6
7
8
)
]
[ B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} ]
[B=(5768)]
沿着第0维度(行)拼接,会将B的行追加到A的行后面:
[
cat
(
A
,
B
,
dim
=
0
)
=
(
1
2
3
4
5
6
7
8
)
]
[ \text{cat}(A, B, \text{dim} = 0) = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ 7 & 8 \end{pmatrix} ]
[cat(A,B,dim=0)=
13572468
]
沿着第1维度(列)拼接,会将B的列追加到A的列后面:
[
cat
(
A
,
B
,
dim
=
1
)
=
(
1
2
5
6
3
4
7
8
)
]
[ \text{cat}(A, B, \text{dim} = 1) = \begin{pmatrix} 1 & 2 & 5 & 6 \\ 3 & 4 & 7 & 8 \end{pmatrix} ]
[cat(A,B,dim=1)=(13245768)]
4.1.2、三维张量
假设我们有两个张量
A
A
A 和
B
B
B,它们的形状都是 [3,5,4]。
这里我们使用以下符号表示它们的元素:
A
=
a
i
j
k
A=a_{ijk}
A=aijk ;
B
=
b
i
j
k
B=b_{ijk}
B=bijk
其中
i
i
i 的范围是 [0,2],
j
j
j 的范围是 [0,4],
k
k
k 的范围是 [0,3]。
按 0 维度拼接
当我们沿着第 0 维度拼接时,新张量
C
C
C 的形状变为 [6,5,4]。
具体来说,新张量
C
C
C 的元素定义如下:
[
C
i
j
k
=
{
a
i
j
k
if
i
<
3
b
(
i
−
3
)
j
k
if
i
≥
3
]
[ C_{ijk} = \begin{cases} a_{ijk} & \text{if } i < 3 \\ b_{(i-3)jk} & \text{if } i \geq 3 \end{cases} ]
[Cijk={aijkb(i−3)jkif i<3if i≥3]
这意味着新张量
C
C
C 的前 3 个切片是
A
A
A 的所有元素,接下来的 3 个切片是
B
B
B 的所有元素。
按 1 维度拼接
当我们沿着第 1 维度拼接时,新张量
D
D
D 的形状变为 [3,10,4]。
具体来说,新张量
D
D
D 的元素定义如下:
[
D
i
j
k
=
{
a
i
(
j
k
)
if
j
<
5
b
i
(
j
−
5
)
k
if
j
≥
5
]
[ D_{ijk} = \begin{cases} a_{i(jk)} & \text{if } j < 5 \\ b_{i(j-5)k} & \text{if } j \geq 5 \end{cases} ]
[Dijk={ai(jk)bi(j−5)kif j<5if j≥5]
这意味着新张量
D
D
D 的前 5 列是
A
A
A 的所有列,接下来的 5 列是
B
B
B 的所有列。
按 2 维度拼接
当我们沿着第 2 维度拼接时,新张量
E
E
E 的形状变为 [3,5,8]。
具体来说,新张量
E
E
E 的元素定义如下:
[
E
i
j
k
=
{
a
i
j
(
k
)
if
k
<
4
b
i
j
(
k
−
4
)
if
k
≥
4
]
[ E_{ijk} = \begin{cases} a_{ij(k)} & \text{if } k < 4 \\ b_{ij(k-4)} & \text{if } k \geq 4 \end{cases} ]
[Eijk={aij(k)bij(k−4)if k<4if k≥4]
这意味着新张量
E
E
E 的前 4 个深度切片是
A
A
A的所有深度切片,接下来的 4 个深度切片是
B
B
B 的所有深度切片。
4.1.3、具体实例
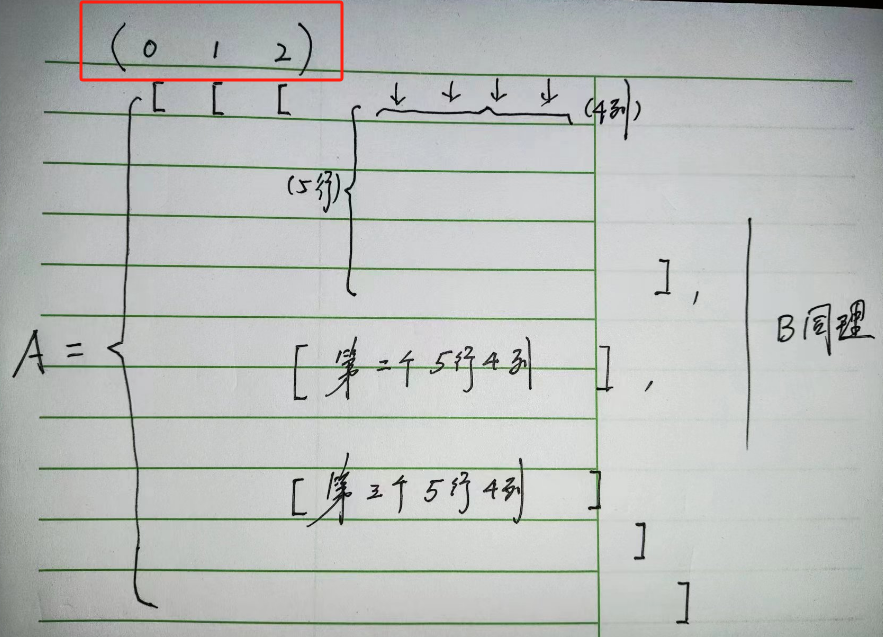
为了更好地理解,我们举个例子。假设:
A
=
(
(
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
)
(
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
)
(
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
)
)
A = \begin{pmatrix} \begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \\ 17 & 18 & 19 & 20 \end{pmatrix} \\ \begin{pmatrix} 21 & 22 & 23 & 24 \\ 25 & 26 & 27 & 28 \\ 29 & 30 & 31 & 32 \\ 33 & 34 & 35 & 36 \\ 37 & 38 & 39 & 40 \end{pmatrix} \\ \begin{pmatrix} 41 & 42 & 43 & 44 \\ 45 & 46 & 47 & 48 \\ 49 & 50 & 51 & 52 \\ 53 & 54 & 55 & 56 \\ 57 & 58 & 59 & 60 \end{pmatrix} \end{pmatrix}
A=
1591317261014183711151948121620
2125293337222630343823273135392428323640
4145495357424650545843475155594448525660
;
B
=
(
(
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
)
(
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
)
(
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
)
)
B = \begin{pmatrix} \begin{pmatrix} 101 & 102 & 103 & 104 \\ 105 & 106 & 107 & 108 \\ 109 & 110 & 111 & 112 \\ 113 & 114 & 115 & 116 \\ 117 & 118 & 119 & 120 \end{pmatrix} \\ \begin{pmatrix} 121 & 122 & 123 & 124 \\ 125 & 126 & 127 & 128 \\ 129 & 130 & 131 & 132 \\ 133 & 134 & 135 & 136 \\ 137 & 138 & 139 & 140 \end{pmatrix} \\ \begin{pmatrix} 141 & 142 & 143 & 144 \\ 145 & 146 & 147 & 148 \\ 149 & 150 & 151 & 152 \\ 153 & 154 & 155 & 156 \\ 157 & 158 & 159 & 160 \end{pmatrix} \end{pmatrix}
B=
101105109113117102106110114118103107111115119104108112116120
121125129133137122126130134138123127131135139124128132136140
141145149153157142146150154158143147151155159144148152156160
- 按 0 维度拼接:
[ C = ( A 1 , : , : A 2 , : , : A 3 , : , : B 1 , : , : B 2 , : , : B 3 , : , : ) ] [ C = \begin{pmatrix} A_{1,:,:} \\ A_{2,:,:} \\ A_{3,:,:} \\ B_{1,:,:} \\ B_{2,:,:} \\ B_{3,:,:} \end{pmatrix} ] [C= A1,:,:A2,:,:A3,:,:B1,:,:B2,:,:B3,:,: ]
- 按 1 维度拼接:
[ D = ( A : , 1 , : B : , 1 , : A : , 2 , : B : , 2 , : A : , 3 , : B : , 3 , : A : , 4 , : B : , 4 , : A : , 5 , : B : , 5 , : ) ] [ D = \begin{pmatrix} A_{:,1,:} & B_{:,1,:} \\ A_{:,2,:} & B_{:,2,:} \\ A_{:,3,:} & B_{:,3,:} \\ A_{:,4,:} & B_{:,4,:} \\ A_{:,5,:} & B_{:,5,:} \end{pmatrix} ] [D= A:,1,:A:,2,:A:,3,:A:,4,:A:,5,:B:,1,:B:,2,:B:,3,:B:,4,:B:,5,: ]
- 按 2 维度拼接:
[ E = ( A : , : , 1 B : , : , 1 A : , : , 2 B : , : , 2 A : , : , 3 B : , : , 3 A : , : , 4 B : , : , 4 ) ] [ E = \begin{pmatrix} A_{:,:,1} & B_{:,:,1} \\ A_{:,:,2} & B_{:,:,2} \\ A_{:,:,3} & B_{:,:,3} \\ A_{:,:,4} & B_{:,:,4} \end{pmatrix} ] [E= A:,:,1A:,:,2A:,:,3A:,:,4B:,:,1B:,:,2B:,:,3B:,:,4 ]
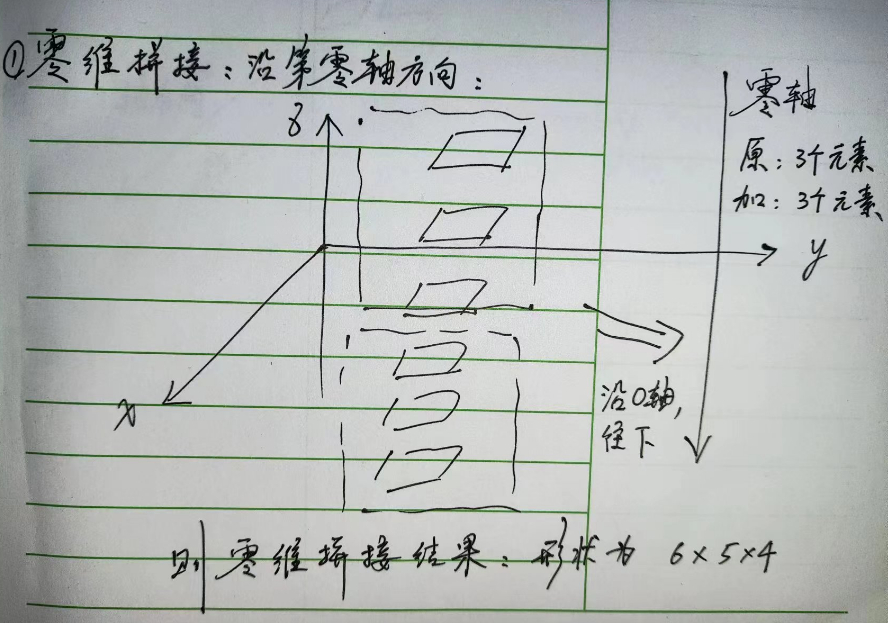
这么看也许还是有些抽象,下面用画图的形式帮助理解。
三个轴由内到外:
零维拼接:
一维拼接:
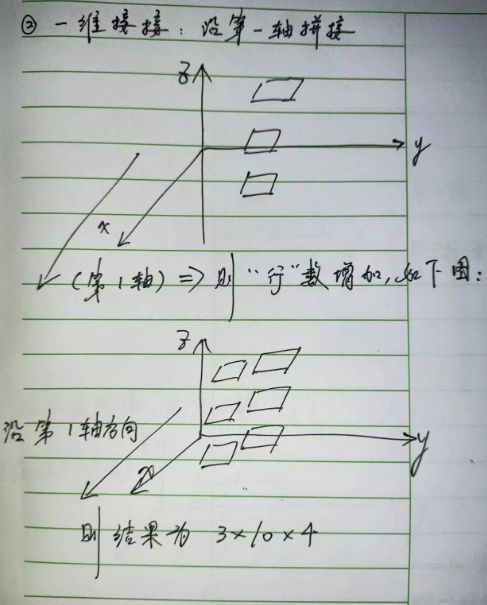
二维拼接:
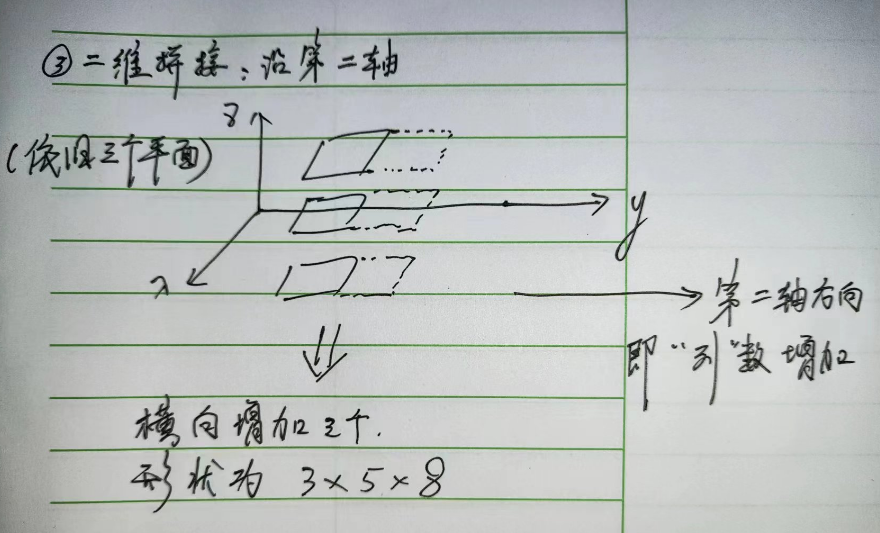
4.2、维度叠加
维度叠加中的0维、1维、2维叠加具体描述了在多维张量(tensor)操作中,如何将多个张量沿某个特定维度堆叠成一个新的更高维度的张量。通过例子和相应的 LaTeX 表达式,可以更清晰地理解这些操作。
维度叠加的概念
假设我们有两个形状相同的张量 A 和 B,形状为 [𝑑0,𝑑1,𝑑2][d0,d1,d2]。
维度叠加就是在现有维度基础上增加一个新的维度来合并这些张量。
假设矩阵
A
A
A 和
B
B
B 为:
A
=
(
1
2
3
4
5
6
)
A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}
A=(142536) ;
B
=
(
7
8
9
10
11
12
)
B = \begin{pmatrix} 7 & 8 & 9 \\ 10 & 11 & 12 \end{pmatrix}
B=(710811912)
4.2.1、0维叠加
0维叠加表示在新增加的第0维度上堆叠多个张量。这会在现有张量的前面增加一个新维度。
操作:
C
=
s
t
a
c
k
(
A
,
B
,
d
i
m
=
0
)
C=stack(A,B,dim=0)
C=stack(A,B,dim=0)
结果:
C
=
(
(
1
2
3
4
5
6
)
(
7
8
9
10
11
12
)
)
C = \begin{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} \\ \begin{pmatrix} 7 & 8 & 9 \\ 10 & 11 & 12 \end{pmatrix} \end{pmatrix}
C=
(142536)(710811912)
新张量形状:[2,2,3]
4.2.2、1维叠加
1维叠加表示在第1维度上堆叠多个张量。这会在现有张量的第二个维度上增加一个新维度。
操作:
C
=
s
t
a
c
k
(
A
,
B
,
d
i
m
=
1
)
C=stack(A,B,dim=1)
C=stack(A,B,dim=1)
结果:
C
=
(
(
1
2
3
)
(
7
8
9
)
(
4
5
6
)
(
10
11
12
)
)
C = \begin{pmatrix} \begin{pmatrix} 1 & 2 & 3 \end{pmatrix} & \begin{pmatrix} 7 & 8 & 9 \end{pmatrix} \\ \begin{pmatrix} 4 & 5 & 6 \end{pmatrix} & \begin{pmatrix} 10 & 11 & 12 \end{pmatrix} \end{pmatrix}
C=((123)(456)(789)(101112))
新张量形状:[2,2,3]
4.2.3、2维叠加(非常重要⭐)
2维叠加表示在第2维度上堆叠多个张量。这会在现有张量的第三个维度上增加一个新维度。
操作:
C
=
s
t
a
c
k
(
A
,
B
,
d
i
m
=
2
)
C=stack(A,B,dim=2)
C=stack(A,B,dim=2)
结果:
C
=
(
(
1
7
2
8
3
9
)
(
4
10
5
11
6
12
)
)
C = \begin{pmatrix} \begin{pmatrix} 1 & 7 \\ 2 & 8 \\ 3 & 9 \end{pmatrix} & \begin{pmatrix} 4 & 10 \\ 5 & 11 \\ 6 & 12 \end{pmatrix} \end{pmatrix}
C=
123789
456101112
新张量形状:[2,3,2]
前面的都好理解,不再展开,
下面详解如何二位叠加。
维度叠加中的二维叠加意味着在第三个维度上堆叠张量。
这种叠加方式实际上增加了一个新维度,将两个张量的对应元素组合在一起。
具体来说,对于每个位置
(
i
,
j
)
(i,j)
(i,j),新的张量在该位置上包含两个元素,一个来自
A
A
A,一个来自
B
B
B。
计算步骤:
对于位置 (1,1):
A
11
=
1
,
B
11
=
7
A_{11}=1,B_{11}=7
A11=1,B11=7
在2维叠加之后,新张量在位置 (1,1) 上的元素为:
C
11
=
(
1
7
)
C_{11} = \begin{pmatrix} 1 \\ 7 \end{pmatrix}
C11=(17)
对于位置 (1,2):
A
12
=
2
,
B
12
=
8
A_{12}=2,B_{12}=8
A12=2,B12=8
在2维叠加之后,新张量在位置 (1,2) 上的元素为:
C
12
=
(
2
8
)
C_{12}=\begin{pmatrix} 2 \\ 8 \end{pmatrix}
C12=(28)
对于位置 (1,3):
A
13
=
3
,
B
13
=
9
A_{13}=3,B_{13}=9
A13=3,B13=9
在2维叠加之后,新张量在位置 (1,3) 上的元素为:
C
13
=
(
3
9
)
C_{13}=\begin{pmatrix} 3 \\ 9 \end{pmatrix}
C13=(39)
继续这样处理所有位置,得到新的张量
C
C
C 的形状为 [2,3,2],每个位置上的元素包含两个来自原始张量的元素。
新张量
C
C
C 的具体表示:
C
=
(
(
1
7
2
8
3
9
)
(
4
10
5
11
6
12
)
)
C = \begin{pmatrix} \begin{pmatrix} 1 & 7 \\ 2 & 8 \\ 3 & 9 \end{pmatrix} \\ \begin{pmatrix} 4 & 10 \\ 5 & 11 \\ 6 & 12 \end{pmatrix} \end{pmatrix}
C=
123789
456101112




![[240720] X-CMD 发布 v0.4.1:新增 OpenAI GPT-4o mini 模型|优化 df ip dns ...](https://i-blog.csdnimg.cn/direct/27d600b657b94b8da4fcfcd9876d7495.png#pic_center)