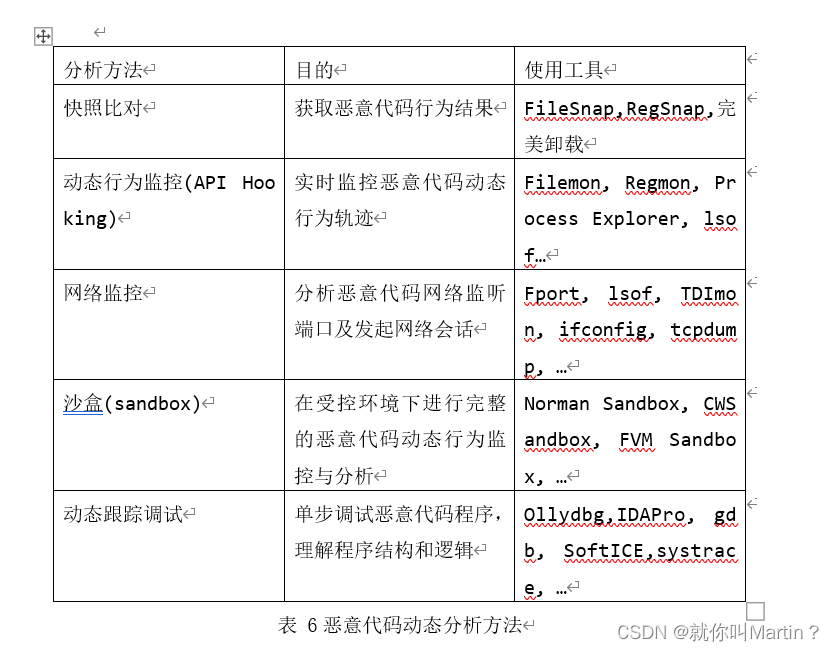
二叉树的一些概念：

//二叉树有严格的左右子树之分，度数为2的树则没有对此进行要求。

常见的两种二叉树：

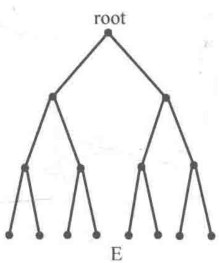
//如上E为满二叉树，每一层的结点个数都达到了当层能达到的最大结点数

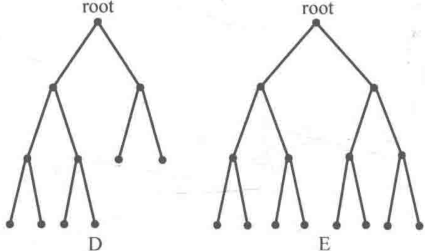
//满二叉树自上而下，从左到右依次进行编号，当且仅当二叉树中的每一个结点的编号都与该满二叉树的结点的编号一一对应，称之为完全二叉树

//理论上可以使用数组来存储完全二叉树，用数组下标作为结点编号，则该结点的左子树就为2*x, 2*x+1,可以找到它的左右结点

//不能通过该结点的编号来进行判断是否为叶子结点，因为只有最右边的结点的编号等于结点个数，最后一层的其他结点的编号都是小于结点数的，因此无法判断，一般通过判断其左子树的编号是否大于结点个数即可，为什么不用判断右子树，因为没有必要，如下图编号为4的结点，左子树的编号即为8，大于7，最小的编号都大于了，右子树肯定也大于了，没必要判断

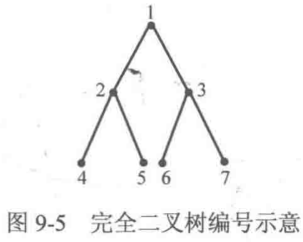
完全二叉树：

①完全二叉树的定义：完全二叉树是指完全填充的树，但底层可能除外，底层是从左到右填充的。

②完全二叉树的存储除了用二叉链表存储以外还可以用更方便的数组进行存储，从1开始（根节点下标,1号位存放的必须是根节点），到n，下标为其结点的编号，值为权重。

这样就有：完全二叉树中任意一个结点编号为x，则左节点一定是2x，右节点的编号一定是2x+1

除以以外，该数组中元素的存放顺序恰好是该完全二叉树的层序遍历序列。

二叉树的查找、修改、插入与删除

//

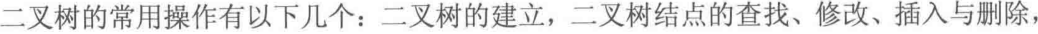
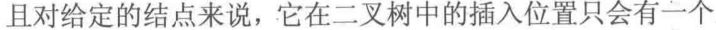
//修改指针就需要加引用修改指针本身，如果是修改指针所指向的内容就没必要，按值传参使用指针的副本即可。

//

//

二叉树的遍历

(11条消息) 二叉树的性质和遍历_柘木木的博客-CSDN博客

//遍历顺序中，左子树一定先于右子树，所谓“先中后”苏配置的是跟接待你在遍历中的位置

先序遍历：（根左右）

//得到的先序遍历的序列为ABDECF

//由图我们可以知道A的子树有哪些结点，右子树有哪些结点，如果只给出一个序列，则我们不能知道左子树的序列多有长，也就不知道右子树的根节点是多少，因此不能确定一棵树

中序遍历：（左根右）

//同样使用该图，得到的中序遍历DBEACF

//通过中序遍历序列区分左右子树序列，通过先序遍历或者后序遍历序列或者层序遍历序列确定根节点

后序遍历：（左右根）

//后序遍历得到的序列为：DEBFCA

//利用层序遍历找到根节点，中序遍历分出左右子树，知道左右子树序列长度放到层序遍历序列中又能找出，左右子树的根节点，这样子一个个根节点找出来，从上到下确定一颗二叉树。

//要保证所有元素不相同，否则可能会找错根节点从而分错左右子树