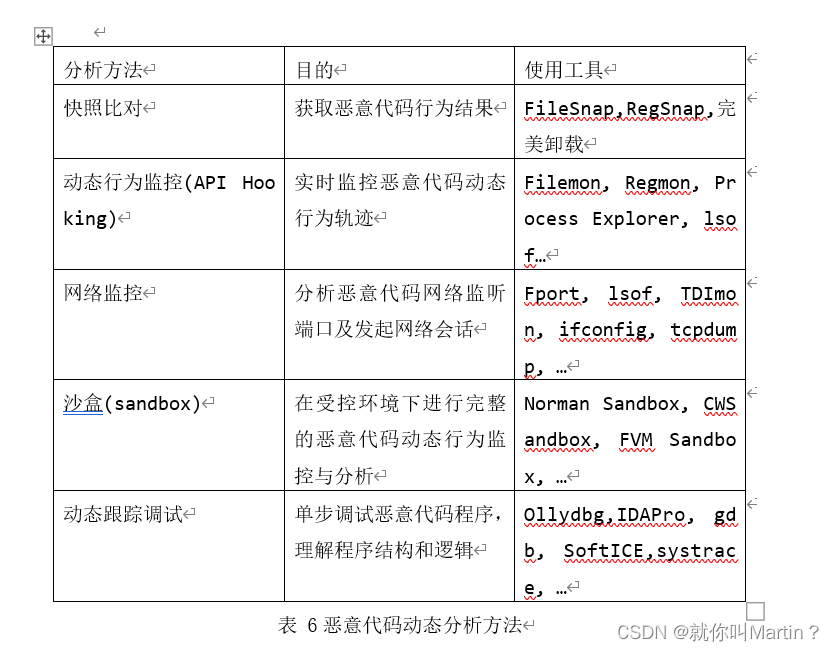
自己琢磨半天终于搞懂了，可能是自己悟性不够吧-_-||

多路数组聚集其实就是对维度(dimension)进行选择，保留一些常用的可以很方便地生成别的子立方体的立方体(cube)。对一个维做聚集(aggregation)其实就是按照这个维度的方向做加法，把这个维度的值缩减成一个。比如3D的按照某一维降成2D,最终降成0D的也就是数多维数组里面非零元素的个数了（假设数组元素是0-1）。
当把多维数组文件分割成可以放进内存的块(chuck)时，我们希望尽可能减少需要重新载入块的操作，也就是减少I/O，尽可能需要这块的操作都一次过完成。也就是每个块只是被载入一次。这个是很容易做到的，但是不同的块载入顺序在维度聚集的时候会需要不同的缓存大小，而各个维度的聚集是同时进行的，所以需要一个合适的载入块的顺序使得所需要的缓存最小。
比如，一个三维的立方体ABC，我们要聚集成AB、AC、BC三个二维的立方体，这三个聚集是同时做的，所以按照什么样的顺序载入chuck会影响到这三个聚集中间数据要保存时间的长短，进而影响所需要的缓存到小（因为需要保存中间结果越多，所需缓存越大）。
如果A、B、C的基数分别是40，400，4000，每个维度分4段，一段构成一个chuck的边。那么chuck取的顺序应该是按照基数由小到大的维度，也就是先A后B再C。
在计算BC面的内存空间时，需要注意的是：从1号小立方体开始遍历计算，然后计算到4号完成对b0c0这个面的所有计算，在计算完1号时，可以放在100×1000的内存空间上，计算完2号，与之前存储的数据匹配相加，然后丢弃即可（只保存加后的最终结果），按照这个逻辑计算完4号就是最终b0c0的结果，取出然后清空，再计算b0c1
我之前一直没有很明白这个蕴含的逻辑，从网上找了一些人的说法也感觉云里雾里，想明白了之后才发现可能是这个太简单了作者可能以为所有人都会（-_-||）。
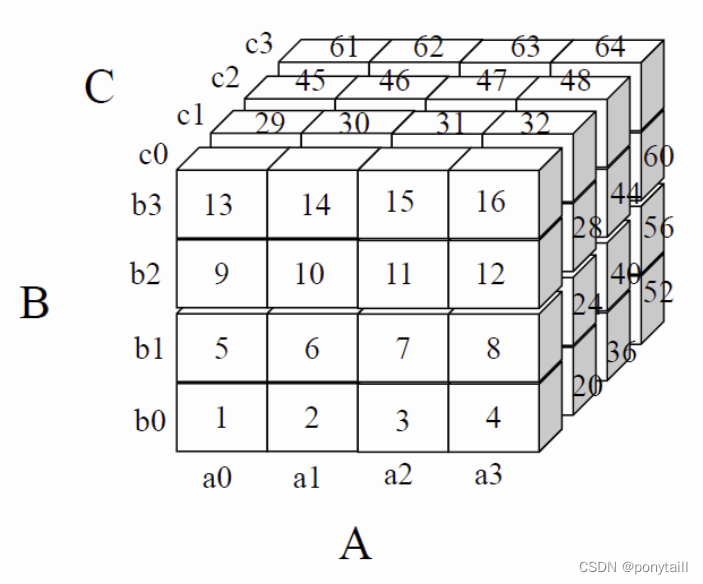同理，再计算AC面时，完成a0c0的所有计算需要等到13号小立方体遍历完，然后14/15/16每块都会完成一个块的计算，我们需要保留从1到12每块的计算结果，也就是向下投影4个a0c0的面积，这样才能最小的保存计算过程（再通俗一点，就是4个块，一个块记录1/5/9相加，一个块记录2/6/10相加等等），因此结果为40×1000
同理，AB面需要保存所有的AB块面积，结果为40×400
此时需要预留的总内存的大小是：16000+40000+100000 = 156000
看完如果有不懂的地方，欢迎评论或者私信我交流。