Paper题目：Topology-based individual tree segmentation for automated processing of terrestrial laser scanning point clouds

ABSTRACT

地面激光扫描 (TLS) 是一种基于地面的方法，可通过光探测和测距 (LiDAR) 技术快速获取 3D 点云。从 TLS 点云量化树尺度结构需要分割，但森林生态社区缺乏可用的自动化方法。在这项工作中，我们考虑将森林 TLS 点云分割成单个树点云的问题。已经研究了不同的方法来识别和分割森林点云中的个别树木。通常这些方法需要大量的参数调整和耗时的用户交互，这阻碍了 TLS 在大面积研究中的应用。我们的目标是定义一种新的自动分割方法来解除这些限制。

我们的基于拓扑的树分割(TTS)算法使用一种基于离散Morse理论的新拓扑技术将输入点云分割成单棵树。TTS算法在没有用户交互的情况下识别独特的树结构(即，树的底部和顶部)。然后，使用相关拓扑特征的概念，使用树顶和树底来重建单棵树。这个在数学上已经确立的概念有助于区分噪声和相关的树特征。

为了证明我们方法的通用性，我们使用多个数据集（包括不同的森林类型和点密度）进行评估。我们还将我们的 TTS 方法与开源树分割方法进行了比较。实验表明，我们在执行逐点验证时实现了更高的分割精度。在没有昂贵的用户交互的情况下，TTS 算法有望在森林生态社区中更多地使用 TLS 点云，例如火灾风险和行为建模、估计树木级生物多样性结构特征和地上生物量监测。

1. Introduction

森林清查是追踪森林结构、生物量和生态状况的基本工具。由于人工实地调查昂贵、耗时且存在潜在危险（Zhen 等人，2016 年），因此已采用遥感技术来协助生成森林清单。其中，光探测和测距 (LiDAR) 允许通过发射激光信号的传感器收集有关森林的详细信息，并根据返回的激光脉冲的时间延迟计算距离。地面 LiDAR，也称为地面激光扫描，可以扫描周围环境并生成数十亿个三维 (3D) 点，从中可以生成树木指标，例如位置、高度和直径 (Liang et al, 2018)，以及树木模型 (Raumonen et al, 2013; Hackenberg et al, 2015a,b) 可以导出。

要运行此类分析，首先需要识别点云中的每一棵树。然而，不一致的点云质量、多样化的森林结构和复杂的植物形态使得很难找到通用、高效和全自动的解决方案（Wilkes 等人，2017 年；Liang 等人，2018 年；Calders 等人，2020 年；Martin -Ducup 等人，2021 年）。

大多数个体树分割方法旨在通过添加外部信息（例如异速生长函数（Burt et al, 2019）、用户定义的参数（Trochta et al, 2017）或人工检查和校正）从输入森林点云中提取单树点云分割结果（Burt 等人，2019 年；Raumonen 等人，2015 年；Calders 等人，2015 年）。同时，外部信息使算法数据集变得特定，难以泛化，并且只能由知识渊博的专家使用。

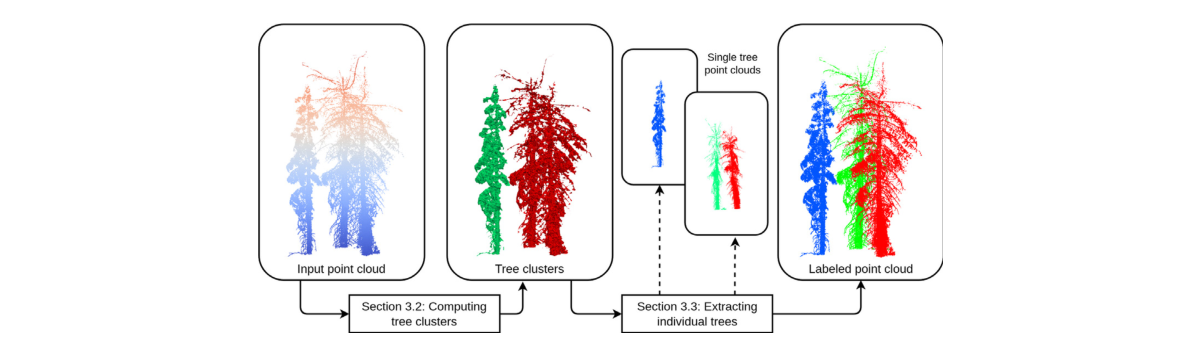
图 1. 所提出的基于拓扑的树分割 (TTS) 方法的流程。输入植被点云被划分为树簇（见第 3.2 节）。然后从每个树簇中提取单个树点云（参见第 3.3 节），它由最终标记的点云组成。单树提取可以并行执行，用虚线箭头标记。

这项工作旨在定义一种自动化方法，能够在不需要用户交互的情况下提供可靠的结果。为了实现这一目标，我们定义了一种新方法，称为基于拓扑的树分割 (TTS)。 TTS 识别森林中独特的结构，如树底和树顶，并使用通过离散莫尔斯理论定义的拓扑结构提取单棵树 (Forman, 1998)。

TTS 的性能在不同的森林类型（即针叶林和落叶林）和点特征（例如点密度）上得到证明。我们还将我们的 TTS 方法与公共领域中可用的最先进方法进行比较，即 3D 森林（Trochta 等人，2017 年）和森林结构复杂性工具 (FSCT)（Krisanski 等人，2021a）。多级验证旨在检查树木识别和树木分割的分割结果。在没有任何参数调整过程的情况下，TTS 表现出卓越的性能，证明非常适合广泛的森林分析应用，包括森林清查、树木建模和地上生物量估算。我们的主要贡献如下：

1. 一种基于拓扑的新型自动分割方法，用于 TLS 点云上的单个树分割。
2. 使用ground truth数据对不同森林类型进行广泛的实验评估。
3. 与两种最先进的开源方法进行个体树分割的客观比较。
4. 证明了所提出的方法对不同森林和点特征（即森林类型、茎密度和点密度）的稳健性。

在本文的其余部分安排如下。在第 2 节中，我们介绍了相关工作。在第 3 节中，我们介绍了所提出的 TTS 方法的工作流程。实验结果和内部参数设置分别在第 4 节和第 5 节中讨论。我们在第 6 节中得出一些结论性意见。

2. Related work

将森林 TLS 点云分割成单个树点云称为单个树分割（Calders 等人，2020）或单个树隔离（Martin-Ducup 等人，2021）。尽管对于包含许多树木的区域而言，手动分割既费时又费力，甚至不可行（Martin-Ducup 等人，2021 年；Burt 等人，2019 年），但仅开发了几种算法来自动执行单个树木分割过程。大多数自动化的个体树木分割方法都是自下而上的，这意味着它们从树底识别和种植树木。由于 TLS 点云是从地面扫描的，因此树干表面点通常是完整的，树底对于定位树木来说是可靠的 (Calders et al, 2020)。

Trochta 等人（2017）提出了一种自下而上的个体树分割算法。点聚集在平行于地面的切片上。后来，树基被定位为低高度集群。最后，通过将附近的簇与附近的茎合并，从检测到的茎构建单棵树。最后，需要许多用户定义的参数来指导分割。通常，还需要手动调整来清理提取的单树点云。

生态知识已被用于更好的分割结果。例如，代谢标度理论 (West et al, 1997) 已被 Tao et al (2015) 和 Wang (2020) 使用。两部作品都首先生成了点图 (Tao et al, 2015; Wang, 2020)。然后，通过根据图上的最短路径将点分配给检测到的最近树干来形成单树点云，其中路径距离根据代谢理论进行缩放（West 等人，1997）。尽管代谢生态学理论有望成为树木生长的普遍尺度规律，但在将理论应用于实际数据集时，应考虑许多因素，如人口特征和光照 (Tao et al, 2015)。对于 Tao 等人 (2015) 和 Wang (2020) 的两种方法，用户需要定义几个参数，例如确定树的大小和过滤有效结果。因此，学习这些方法和找到合适的设置需要时间。

树木测量之间的异速生长关系也用于分割方法。 Burt 等人 (2019) 基于点云库 (PCL) (Rusu and Cousins, 2011) 开发了一种分割方法，即 treeseg。在检测到树干后，Burt 等人 (2019) 使用树干直径与树高和树冠范围之间的异速生长关系来提取树冠。据我们测试，实施的软件在源代码中硬编码了参数。由于应用了与特定森林相关的异速生长函数，treeseg 可能不适用于开箱即用的数据集。

最近，深度学习工具已应用于 TLS 点云分析。 Krisanski 等人扩展了他们基于深度学习的语义分割方法（Krisanski 等人，2021b）以提取单树点云，并设计了森林结构复杂性工具（FSCT）（Krisanski 等人，2021a）。在 FSCT 中，PointNet++ (Qi et al, 2017) 用于将森林点分类为地形、植被、粗木屑和树干点。树骨架是通过基于密度的聚类方法对树干点进行分组生成的，例如 HDBSCAN（McInnes 等人，2017 年）和 DBSCAN（Ester 等人，1996 年）。通过 RANSAC（Fischler 和 Bolles，1981）进行的圆柱体拟合被重复应用于骨架点以生成代表茎和分支的圆柱体。完整的树结构是通过对相邻的圆柱体进行分组来实现的。最后，将点分配给最近的树圆柱以形成单树点云。由于应用了深度学习工具，FSCT需要大量的计算资源，这也是处理大数据的障碍。除了 PointNet++ (Qi et al, 2017) 之外，还使用了不同的深度学习技术在分割之前从点云中提取树的位置。 Fan 等人 (2022) 关注 TLS 点派生图像，使用 YOLOv3 (DarkNet-53)（Redmon 和 Farhadi，2018）提取树冠边界，Wang 等人（2019）应用 Faster R-CNN（Ren 等人， 2015）来检测中继线位置。 Xi 和 Hopkinson (2021) 使用 CenterNet（Duan 等人，2019 年）在基于体素的点云表示上提取树冠边界。这些方法（Fan 等人，2022 年；Xi 和 Hopkinson，2021 年；Wang 等人，2019 年）虽然很有前途，但在应用深度学习技术之前需要将 3D 点云转换为图像或体素。此外，基于深度学习的方法需要训练大量带注释的数据，而在真实场景中收集这些数据可能具有挑战性（Calders 等人，2020 年）。

3. Topology-based tree segmentation (TTS) approach

所提出的用于个体树分割的 TTS 方法由两个步骤组成。整个管道如图 1 所示。首先，在划分步骤中，我们将输入的植被 TLS 点云分成子区域，称为树簇。直观地说，每个树簇都是一组具有交叉树冠的树（见第 3.2 节）。然后，使用提取步骤通过自下而上的分割方法找到每棵树（参见第 3.3 节）。在本节的其余部分，我们首先简要介绍关于单纯复形、훼-复形和离散莫尔斯理论的背景概念，这有助于理解所提出的方法。

3.1. Discrete morse theory

单纯复形和 𝛼-复形。我们使用单纯复形来推断 3D 点云上的拓扑（即连通性）结构。形式上，𝑘-单纯形𝜎是欧几里德空间中𝑘+ 1个仿射独立点的凸包。例如，0-单纯形是一个点，1-单纯形是直线段，2-单纯形是三角形，3-单纯形是四面体。 𝑘 被称为𝜎 的维度。我们将由顶点 𝑣0、𝑣1、…、𝑣𝑘 跨越的 𝑘-单纯形𝜎 表示为 𝜎 = {𝑣0、𝑣1、…、𝑣𝑘}。任何单纯形 𝜏 是生成单纯形 𝜎 的点的非空子集的凸包，是 𝜎 的面。

单纯复形 𝛴 是一组有限的单纯形，这样：(i) 𝛴 中的一个单纯形的每个面都属于 𝛴； (ii) 对于每对单纯形 𝜎 和 𝜏，𝜎 ∩ 𝜏 = ∅ 或 𝜎 ∩ 𝜏 是两者的面。

𝛼-复形是由 Delaunay 四面体化 𝛴𝑇 的单纯形构成的单纯复形（Delaunay 等人，1934 年）。令 𝜎 是 𝛴𝑇 中的单纯形，并令 𝐶𝜎 是 𝜎 的外接圆（或外接圆），半径为 𝑟。 𝛼-复形 (Edelsbrunner, 2010) 𝛴𝛼 是 𝛴𝇇 的子复形，包含 𝛴𝑇 的所有顶点，加上所有单纯形 𝜎 使得：(i) 𝑟 < 𝛼 和 𝐶𝜎 不包含 𝑃 中的点，或 (ii) 𝜎 是面∈ 𝛴𝛼 .

离散莫尔斯理论。离散莫尔斯理论 (Forman, 1998) 是莫尔斯理论 (Milnor, 1963) 的组合对应物，它允许研究单纯复形 𝛴 的拓扑结构。

𝛼-复形是由 Delaunay 四面体化 𝛴𝑇 的单纯形构成的单纯复形（Delaunay 等人，1934 年）。令 𝜎 是 𝛴𝑇 中的单纯形，并令 𝐶𝜎 是 𝜎 的外接圆（或外接圆），半径为 𝑟。 𝛼-复形 (Edelsbrunner, 2010) 𝛴𝛼 是 𝛴𝇇 的子复形，包含 𝛴𝑇 的所有顶点，加上所有单纯形 𝜎 使得：(i) 𝑟 < 𝛼 和 𝐶𝜎 不包含 𝑃 中的点，或 (ii) 𝜎 是面∈ 𝛴𝛼 .离散莫尔斯理论。离散莫尔斯理论 (Forman, 1998) 是莫尔斯理论 (Milnor, 1963) 的组合对应物，它允许研究单纯复形 𝛴 的拓扑结构。

给定一个单纯复形 𝛴，一个离散向量是一对单纯形 (𝜎, 𝜏)，其中 𝜎 是 𝜏 的一个面。离散向量场 𝑉 是对 (𝜎, 𝜏) 的集合，使得 𝛴 的每个单纯形至多在一对 𝑉 中。不属于任何矢量的单形称为临界单形。在三角形网格中，关键三角形是最大值，关键边是鞍点，关键顶点是最小值。对由一个三角形和一条边组成；以及一条边和一个顶点。 V 路径是一个序列𝜎1, 𝜏1, 𝜎2, 𝜏2, …, 𝜎𝑟, 𝜏𝑟，使得 (𝜎𝑖, 𝜏𝑖) ∈ 𝑉, 𝜎𝑖+1 是 𝜏+𝑖 的脸，以及 𝜎𝑖 和 𝜎𝑖 𝜎𝑖, 𝜏𝑖 𝜎𝑖如果 𝜎1 是 𝜏𝑟 不同于 𝜎𝑟−1 的一个方面，则 𝑟 > 1 的 V 路径是闭合的。如果离散矢量场 𝑉 没有封闭的 V 路径，则称为 Forman 梯度。分线𝑉𝑖-路径是分别连接维度为𝑖 + 1 和𝑖 的两个临界单纯形的𝑉 路径。在三角形网格中，我们有每个分隔线𝑉0-路径将关键边连接到关键顶点，以及分隔线𝑉1-路径将关键三角形连接到关键边。

当根据输入标量函数 𝑓 ∶ 𝛴 → R 计算离散梯度 𝑉 时，𝑉 可以作为 𝑓 梯度及其临界点的组合表示。例如，图 2(a) 显示了在三角形网格 𝛴 上定义的标量函数 𝑓。图 2(b) 显示的箭头表示梯度对，而点表示关键单纯形。蓝点表示最小值，绿点表示鞍点，红点表示最大值。请注意，所有用箭头表示的梯度对都模仿函数的梯度，指示函数值减小的方向。为此，已经定义了许多方法来计算规则网格上的离散梯度（Guylassy 等人，2008 年；Robins 等人，2011 年；Shivashankar 等人，2012 年；Shivashankar 和 Natarajan，2012 年）和单纯复形（Weiss 等人， 2013 年；Fellegara 等人，2014 年）。 De Floriani 等人 (2015) 对这些方法进行了完整概述。

Forman 梯度根据 𝑓 的关键点的影响区域隐含地定义了 𝛴 的分割（De Floriani 等人，2015）。在这项工作中，我们关注 𝑓 的最小值的影响区域，也称为最小上升区域。最小顶点𝜎的最小上升区域被定义为属于到达𝜎的𝑉0-路径的顶点集合。图 2© 显示了图 2(b) 中 Forman 梯度的最小上升区域。每个顶点都属于表征 𝑉 的四个最小值之一的最小值上升区域（见图 2(b) 中的四个蓝点）。

3.2. Computing tree clusters

在这项工作的其余部分，我们将森林植被点云称为输入点集𝑃。本节介绍的所有参数值将在第 5 节中讨论和激发。

TTS 方法的第一个目标是通过划分易于分离的树来将𝑃 划分为树簇。我们通过在 𝑃 上计算一个 𝛼-复数 𝛴 并找到 𝛴 的连通分量来实现这个目标。

在计算 𝛼 复形时，𝛼 的值会影响 𝛴 的形状和连通分量的数量。因此，目标是获得一个 𝛼 复合体，它勾勒出树的形状（即树枝、树干），同时断开容易分离的树。图 3 显示了用不同 𝛼 值生成的三个𝛼-复合物。当𝛼值很小时，如图3(a)中的𝛼 = 0.02 m，𝛼-complex由孤立的点组成，无法勾勒出树形。然而，图 3（c）中的 𝛼 值较大（𝛼 = 0.3 m）时，树木连接成一个组件，很难分裂。此外，图 3© 中 𝛼-复合体中的木质结构（即树枝、茎）不如图 3(b) 中 𝛼 = 0.1 m 的内置𝛼-复合体清晰。为此，我们的实验将 𝛼𝑠 = 0.1 m 确定为理想值。

一旦计算出 𝛼-复数 𝛴，我们就处理它的连通分量。对于每个组件，我们考虑具有最低高度的顶点和组件的长度。组件长度定义为组件中最高点和最低点之间的高程差。然后，当且仅当其最低顶点的高度小于𝑡ℎ𝑙𝑜𝑤 = 1.5 m 且长度大于𝑡ℎ𝑙𝑒𝑛 = 2 m 时，𝛴 的一个组件才被分类为树簇，以去除噪声和小植被。这导致将森林点细分为树簇。图 4 说明了从具有三棵树的点云计算出的两个树簇。 𝛼-complex 有两个组成部分建立在点云上（见图 4（b））。这两个组件都成功地勾勒出了关键的树木特征，例如树梢的树枝和树干。三棵树被分成两个簇，其中一个簇包括一棵树（见图 4(b) 中的绿点），而另一个簇有两棵树冠相交的紧密树木（见图 4(b) 中的红点） .

3.3. Extracting individual trees

计算树簇后，目标是识别每个簇中的个体树。为此，我们使用基于离散莫尔斯理论（Forman，1998）的自下而上的分割方法。

令 𝛴𝑡𝑐 为对应于树簇的 𝛼-复数成分。我们在𝛴𝑡𝑐的顶点上定义一个标量函数𝑓作为高度函数。形式上，𝑓 (𝑝) = 𝑝.𝑧 其中 𝑝 是 𝛴𝑡𝑐 中的一个顶点，𝑝.𝑧 是它的高程。然后，我们计算对应于𝛴𝑡𝑐 和𝑓 的 Forman 梯度𝑉（见第 3.1 节），我们使用临界点，即最小值，来指导树簇分割。

计算最小上升区域。给定在 𝛴𝑡𝑐 上计算的 Forman 梯度𝑉，我们通过计算对应于𝑓 最小值的影响区域来提取𝛴𝑡𝑐 顶点的分割（参见第 3.1 节）。最小值的影响区域，即最小上升区域，是在Forman梯度中对顶点-边箭头进行广度优先遍历得到的顶点的集合。从最小顶点𝑣 开始，我们将𝑣 插入到队列𝑄 中。在每次迭代中，我们从 𝑄 中提取一个顶点 𝑣1 并计算入射在 𝑣1 中的边。对于每个这样的边，我们检索它们是否与不同于 𝑣1 的某个顶点 𝑣2 配对。如果是这种情况，我们将𝑣2 添加到𝑄。最小顶点𝑣对应的簇是通过收集该次访问接触到的所有顶点得到的。图 5© 显示了从图 5(b) 中所示的最小值计算的最小上升区域。许多最小上升区域意味着树簇点被过度分割。直观上，每个最小值表示一个点相对于相邻点具有最小高程值。对于 𝛼-复数 𝛴𝑡𝑐，最小值对应于树底或树枝朝下（见图 5（b））。因此，计算的最小上升区域仅代表小树组件而不是完整的树。自然地，我们将联合树组件来构建单个树。我们不会直接合并点，而是处理最小值，将同一棵树中的最小值分组，这样每个树点云都可以从同一组最小值上升区域中找到。

找到树的种子。我们首先确定呈现树底的最小值。为了从最小值区分树底和树枝，我们通过删除 𝑡ℎ𝑠𝑡𝑒𝑚 = 0.5 m 以上的所有点和单纯形（即边、三角形和四面体）来裁剪 𝛴𝑡𝑐。我们将剩余的 3-复形称为剪裁单纯形复形，并将其表示为 𝛴′𝑡𝑐。

然后，我们将 𝛴′𝑡𝑐 的每个分量与 𝑉 中的最小值进行匹配。即，如果 𝛴′𝑡𝑐 中的一个分量至少包含一个最小顶点，则该分量称为种子分量，最小值被归类为种子顶点。请注意，一个种子组件可以包含多个最小值作为种子。图 6 显示了从树簇中找到的种子成分和种子顶点。从剪下的 𝛴′𝑡𝑐 中可以很好地捕获两个茎，因为两个种子成分是分离的。每个种子组件包括几个绿色和红色的最小值。

种植单棵树。一旦树被播种，TTS 算法将剩余的最小值与种子相关联，并组合所有点以形成单个树点云。

TTS 仍然使用 Forman 梯度 𝑉 以及之前计算的临界复合体（即最小值和 1-鞍点）。我们计算一个表示最小值和 1-鞍点的连通性的图。更具体地说，从每个最小值开始，我们沿着 𝑉 路径找到它连接的 1-鞍点。如果两个最小值连接到同一个 1-saddle，我们称这些最小值已连接。最后，该图表示为𝐺𝑚 =(𝑁, 𝐴, 𝑅)，其中𝑁 中的节点对应𝑉 中的最小值，如果连接相应的最小值，则𝐴 中的弧连接两个节点。𝑅 是分配给每个种子节点的标签在𝑁。属于同一种子组件的种子节点具有相同的标签。所有剩余的节点都标记为未标记。

然后，我们将 𝑁 中对应于树种子（即标记为种子点的最小值）的所有节点插入有序队列中，使节点按海拔的升序排序。对于从队列中提取的每个节点 𝑛，我们检索 𝐺𝑚 中连接到 𝑛 的节点。对于连接到𝑛的每个未标记节点𝑛𝑏𝑟，我们分配给𝑛𝑏𝑟与𝑛相同的标签（即𝑅（𝑛𝑏𝑟）=𝑅（𝑛）），我们将𝑛𝑏𝑟插入队列。图 7 显示了最小值标记过程。出于说明目的，我们根据 𝑓 值放置种子（分别以红色和蓝色着色）和未标记的黄色节点。由于图 7（a）中红色种子 1 低于蓝色种子 2，我们有一个初始化为 {1, 2} 的队列。我们首先检查红色 seed1 并将其相邻的未标记节点标记为 4 和 7（见图 7（b））。队列变为 {2, 4, 7}。类似地，我们在图 7（c）的下一步中通过合并其相邻的未标记节点 3 和 6 来种植蓝色种子 2。并且，队列 {3, 4, 6, 7} 根据它们的 𝑓 值按升序排列。当我们检查节点 3 和 4 时，分别没有未标记的节点与节点 3 和 4 相邻。因此，没有标记的新节点。队列变为 {6, 7}。最后，我们处理节点 6 并为其分配未标记的节点 5。队列现在有 {5, 7}。但是，节点 5 和 7 的所有邻居节点都已被标记。换句话说，所有节点现在都被标记为如图 7（d）所示。

一旦 𝐺𝑚 中的所有节点都被标记，我们将分配给每个最小值的标签传播到其影响区域，这将开始形成树点云并标记输入聚类点。图 8(a) 和 (b) 分别显示了初始和最终状态的标记最小值。一开始，只有底部的种子被标记，而其余的最小值没有标记。从底部长出树后，其余的最小值被成功分配给带有树标签的树干。基于最小值上升区域，在图 8（c）中标记点，其中从树簇点成功提取了两棵树。

附加稀疏点。生成的 𝛼-complex 𝛴 可能不包括所有树点，特别是对于树梢点稀疏的质量差的点云。通常，在此步骤之前提取的单个树点云将识别树的硬物体（即树干和树枝），但它们可能会错过稀疏的树梢点。最后的提取步骤旨在将稀疏点分配给提取的单棵树。这个想法是通过修改 𝛼-complex 来扩展点标记。为了确保所有点的连通性，我们生成了一个新的 𝛼-complex 𝛴𝑙 整个森林点𝑃 具有更大的 𝛼 值（即 𝛼𝑙 = 0.3 m）。然后，我们使用 𝛴𝑙𝑔 中编码的连通性重复使用相同的贪心搜索（如图 7 所示），将遗漏点添加到每个提取的单树点云中。图 9 显示了在最后一步之后分割的树的示例。两棵树完全是从树的聚类点中提取出来的。如图 9© 所示，在图 9(b) 中正确添加了遗漏的稀疏树梢点。

6. Concluding remarks

我们提出了一种通用的、稳健的、自动化的基于拓扑的树分割 (TTS) 方法，用于森林 TLS 点云，具有 훼-complex 和 Forman 理论。我们的即插即用方法也被证明可以在不同的开箱即用数据集上工作而无需参数调整。但是，需要在更广泛的森林、TLS 仪器和调查属性中进行测试。

我们设计了具有多层次验证的实验。通过计算三个指标，已使用标记的 TLS 点云来逐点检查提取的单点云：Rand 指数、方向汉明距离和平均交叉并集 (IoU)。在实验中，我们将 TTS 方法与开源方法 3D Forest（Trochta 等人，2017 年）和 FSCT（Krisanski 等人，2021a）进行了比较。结果证明，无论森林类型、茎密度和输入 TLS 点云的点密度如何，TTS 都能提供更好的精度。 TTS 达到了最高的平均兰德指数 0.96，方向汉明距离为 0.90，平均 IoU 为 0.78，这表明分割结果非常准确。此外，TTS 不需要用户定义的参数，可以直接在不同的森林和数据集中工作。连同可靠性和通用性，TTS 有望更多地使用 TLS 点云，例如火灾风险和行为建模、估计树级生物多样性结构特征和地上生物量监测。

我们计划在未来以不同的扫描设计在更多森林上测试 TTS。为此，迫切需要带有标记树点的公共 TLS 点云。考虑到由于 TLS 点云中的阴影和重叠树枝导致的点密度变化（Trochta 等人，2017 年），正在研究基于加权 Delaunay 三角剖分的 α-复数（Edelsbrunner，2010 年），其范围是改进树形描绘和分割表现。我们从茎生长的区域也有望受益于代谢缩放理论 (West et al, 1997)，该理论也被用于 Tao 等人 (2015) 和 Wang (2020) 的个体树木分割工作中。最后，我们的方法的计算性能也在并行工作中得到解决。由于我们的分而治之策略，我们的方法自然支持并行计算，并极大地提高了计算性能。对于可扩展性问题，我们将使用分布式数据结构，如 Stellar 树 (Fellegara et al, 2021) 来处理从大点云构建的大型 α 复合体。