文章目录
- 拓扑排序
- [P1113 杂务](https://www.luogu.com.cn/problem/P1113)
- 题目描述
- 输入格式
- 输出格式
- 代码(BFS)
- [P4017 最大食物链计数](https://www.luogu.com.cn/problem/P4017)
- 题目描述
- 输入格式
- 输出格式
- 代码(BFS)
- 代码(DFS)
- [P1983 [NOIP2013 普及组] 车站分级](https://www.luogu.com.cn/problem/P1983)
- 题目
- 代码
拓扑排序
一个图能进行拓扑排序的充要条件是它是有向无环图(DAG)。有入度,出度的概念。BFS,DFS 都能实现。
** BFS **
分为无前驱和无后继的顶点优先。
无前驱
1.先找到入度为零的顶点,入队
2.弹出队首,将其邻居点入度-1,入度=0,入队
3.循环2,直到为空
无解说明不是DAG,未入队的是环路上的点。
P1113 杂务
题目描述
John 有需要完成的 n n n 个杂务的清单,并且这份清单是有一定顺序的,杂务 k ( k > 1 ) k\ (k>1) k (k>1) 的准备工作只可能在杂务 1 1 1 至 k − 1 k-1 k−1 中。(由于这个,此题不用拓扑也很简单)
写一个程序依次读入每个杂务的工作说明。计算出所有杂务都被完成的最短时间。当然互相没有关系的杂务可以同时工作,并且,你可以假定 John 的农场有足够多的工人来同时完成任意多项任务。
输入格式
第1行:一个整数 n ( 3 ≤ n ≤ 10 , 000 ) n\ (3 \le n \le 10{,}000) n (3≤n≤10,000),必须完成的杂务的数目;
第 2 2 2 至 n + 1 n+1 n+1 行,每行有一些用空格隔开的整数,分别表示:
- 工作序号(保证在输入文件中是从 1 1 1 到 n n n 有序递增的);
- 完成工作所需要的时间 l e n ( 1 ≤ l e n ≤ 100 ) len\ (1 \le len \le 100) len (1≤len≤100);
- 一些必须完成的准备工作,总数不超过 100 100 100 个,由一个数字 0 0 0 结束。有些杂务没有需要准备的工作只描述一个单独的 0 0 0。
保证整个输入文件中不会出现多余的空格。
输出格式
一个整数,表示完成所有杂务所需的最短时间。
代码(BFS)
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int ind[500005],f[500005],a[500005];
vector<int> e[500005];
queue<int> q;
signed main()
{
IOS
int n,b,c;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>b>>a[i];
while(cin>>c&&c!=0)
{
e[c].push_back(i);//e存放出度编号
ind[i]++;//ind计算入度个数
}
}
for(int i=1;i<=n;i++)//找到入度为零的点存入队列
if(ind[i]==0)
{
q.push(i);
f[i]=a[i];//完成时间就是单个任务的完成时间
}
while(!q.empty())
{
int r=q.front();//推出的第一个
q.pop();
for(int i=0;i<e[r].size();i++)
{
int u=e[r][i];
ind[u]--;//将r指向的编号入度-1
if(ind[u]==0) q.push(u);
f[u]=max(f[u],f[r]+a[u]); //最大的时间是某杂物的完成时间
}
}
int ans=0;
for(int i=1;i<=n;i++)
ans=max(ans,f[i]);
cout<<ans<<'\n';
return 0;
}
P4017 最大食物链计数
题目描述
给你一个食物网,你要求出这个食物网中最大食物链的数量。
(这里的“最大食物链”,指的是生物学意义上的食物链,即最左端是不会捕食其他生物的生产者,最右端是不会被其他生物捕食的消费者。)
Delia 非常急,所以你只有
1
1
1 秒的时间。
由于这个结果可能过大,你只需要输出总数模上
80112002
80112002
80112002 的结果。
输入格式
第一行,两个正整数 n 、 m n、m n、m,表示生物种类 n n n 和吃与被吃的关系数 m m m。
接下来 m m m 行,每行两个正整数,表示被吃的生物A和吃A的生物B。
输出格式
一行一个整数,为最大食物链数量模上 80112002 80112002 80112002 的结果。
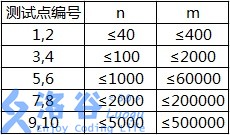
【补充说明】
数据中不会出现环,满足生物学的要求。(感谢 @AKEE )
代码(BFS)
累加,上一个点的答案累加到下一个点。初始为1,最后每一条路都会累加到出度为零的点,再加一块。所以用向量存出度,要到下一个点,接着算(而dfs,要存入度)
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int ind[500005],sum[500005];//ind放入度,sum累加食物链
const int mod=80112002;
//vector<int> ch[500005];
vector<vector<int>> ch;
queue<int> d;
signed main()
{
IOS
ch.resize(500005);
int n,m,a,b,ans=0;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
cin>>a>>b;
ch[a].push_back(b);//a里存放他的天敌,即出度
ind[b]++;
}
for(int i=1;i<=n;i++)
{
if(ind[i]==0)//找到食物链底端
{
d.push(i);
sum[i]++;
}
}
while(!d.empty())
{
int u=d.front();
d.pop();
for(int i=0;i<ch[u].size();i++)
{
ind[ch[u][i]]--;
sum[ch[u][i]]=(sum[ch[u][i]]+sum[u])%mod;//加上它食物的链数
if(ind[ch[u][i]]==0)
{
d.push(ch[u][i]);
}
}
}
for(int i=1;i<=n;i++)
if(ch[i].size()==0)//没有天敌,即顶端加一块
ans=(ans+sum[i])%mod;
cout<<ans<<'\n';
}
代码(DFS)
向量存入度结点,需要递归从后往前,最前端写1,在往后累次加
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
vector<vector<int> > ch;
const int mod=80112002;
int out[500005],sum[500005];//out计算出度,sum计算链数
int dfs(int j)
{
if(ch[j].empty()) //到达食物链底端
{
sum[j]=1;
return 1;
}
for(int i=0;i<ch[j].size();i++)
{
if(sum[ch[j][i]]==0)
sum[j]=(sum[j]+dfs(ch[j][i]))%mod;
else
sum[j]=(sum[j]+sum[ch[j][i]])%mod;//j点链数等于j点加上他的入度链数
}
return sum[j];
}
signed main()
{
ch.resize(500005);
int n,m,x,y,ans=0;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
cin>>x>>y;
out[x]++;
ch[y].push_back(x);
}
for(int i=1;i<=n;i++)
{
if(out[i]==0)//找到顶端
ans=(ans+dfs(i))%mod;
}
cout<<ans;
}
P1983 [NOIP2013 普及组] 车站分级
题目

代码
每个火车,从始到终没停的站点,可以看作已停的入度。
入度为0的开始,level为1,往后累加。出度为0中最大的level为答案。这里用的out数组,开始用的vector,MLE,TLE,还有初始化问题。没成功。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
queue<int> q;
//vector<vector <int> > out;不能用
int out[1005][1005];
int n,m,ind[1005],a[1005],level[1005];
void bfstuopu()
{
for(int i=1;i<=n;i++)
if(ind[i]==0)
{
q.push(i);
level[i]=1;
}
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=1;i<=n;i++)
{
if(out[u][i]==1)
{
ind[i]--;
if(ind[i]==0)
{
q.push(i);
level[i]=level[u]+1;
}
}
}
}
}
signed main()
{
IOS
int s;
cin>>n>>m;
int v[1002];
for(int i=1;i<=m;i++)
{
memset(v,0,sizeof(v));
cin>>s;
for(int j=1;j<=s;j++)
{
cin>>a[j];
v[a[j]]=1;
}
for(int j=a[1];j<=a[s];j++)
if(v[j]==0)
{
for(int k=1;k<=s;k++)
{
if(out[j][a[k]]==0)
// if(find(out[j].begin(),out[j].end(),a[k])==out[j].end()) //加if 不会MLE,但TLE
{
out[j][a[k]]=1;
ind[a[k]]++;
}
}
}
}
bfstuopu();
int ans=1;
for(int i=1;i<=n;i++)
ans=max(ans,level[i]);
cout<<ans;
}
二维vector初始化
vector<vector > vec(10,vector(8))
10行8列,全为0