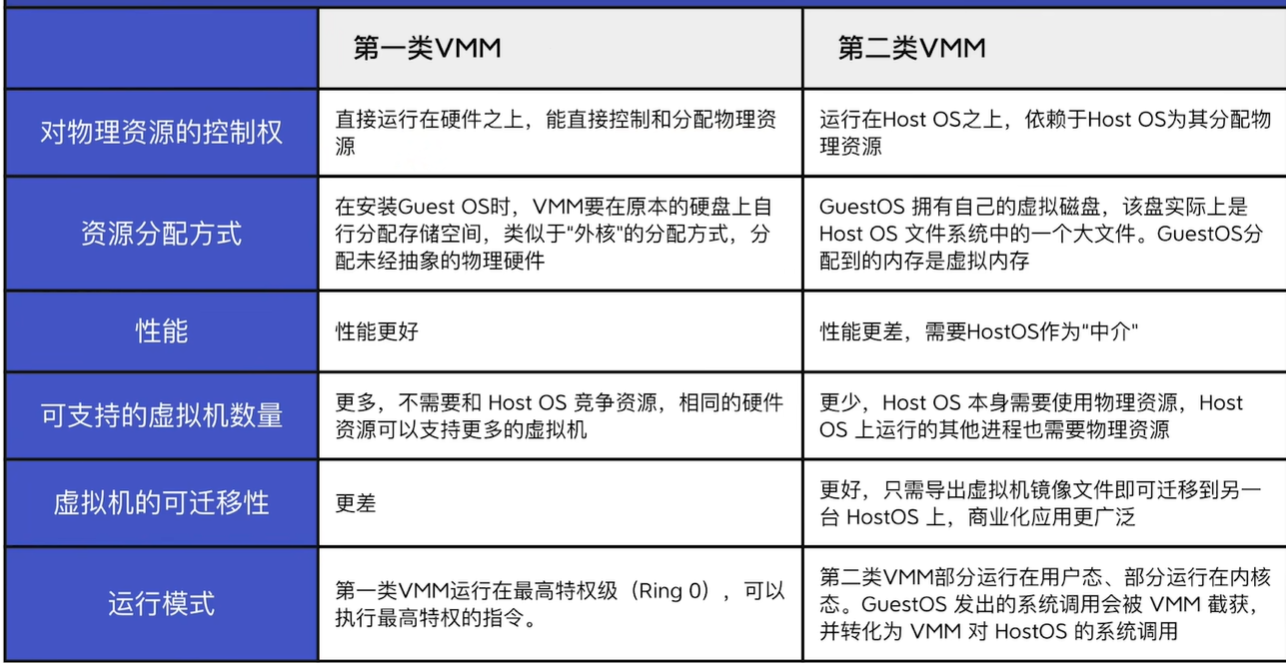
目录
树的定义
树的基本术语
树的初始起点:我们定义为根
树的层次:
树的定义:
树的性质
性质1:
性质2:
树形结构存储的两种思路
树的遍历模板
树上信息统计方式1-自顶向下统计
树上信息统计方式2-自底向上统计
子树的概念:
总结:编辑
树的定义
树(Tree)是n(n≥0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:①有且仅有一个特定的称为根(Root)的结点;②当n>1时,其余结点可分为m(m>0)个互不相交的有限集T 1 {T}_{1}T 1 、T 2 {T}_{2}T 2 、… 、T m {T}_{m}T m ,其中每一个集合本身又是一棵树,并且称为根的子树(Sub Tree)。
树的基本术语
- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 叶节点或终端节点:度为0的节点称为叶节点;
- 非终端节点或分支节点:度不为0的节点;
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 树的度:一棵树中,最大的节点的度称为树的度;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的初始起点:我们定义为根
递归树中,都只能从父节点走到子节点。
我们只需要记录每个父节点有哪些子节点,那么就可以遍历整个递归树。
树的层次:
节点高度:指从这个节点到叶子节点的距离(一共经历了几个节点)
节点深度:指从当前节点到根节点的距离(一共经历了几个节点)
树的高度:指所有节点高度的最大值
树的深度:指所有节点深度的最大值
节点的层:从根节点开始,假设根节点为第1层,根节点的子节点为第2层,依此类推
树的定义:
有n(n>=0)个节点,且任意两个点有且仅有一条路径连通的图形。若n=0,此时为空树。
树的性质
性质1:
n个节点,保证任意两点有且仅有一条路径,树中有且仅有n-1条边。
证明:除第一个节点外,连接一个其他节点,至少增加一条边,所以n个点至少要用n-1条边才能保证所有节点连通。若此时再增加一条非重边,任意两点间是否还存在一条唯一路径。
性质2:
树的根结点没有前驱(父节点),除根结点外的所有结点有且只有一个前驱。树中所有结点可以有零个或多个后继(子节点)。
证明:同上。
树形结构存储的两种思路
1.用结构体把每个节点的信息进行封装。这样的优点在于节点信息非常独立,但是所占空间稍大。2.用多个数组,分别描述每个节点的对应信息。这种方式的有点在于速度稍快,写起来简单。


树的遍历模板
通常来讲,树的边都是双向的我们在遍历的时候不希望一个点遍历多次。
方法1.用vis数组进行标记。
方法2.dfs中记录由父亲节点(来向),这样可以阻止走回去。
树上信息统计方式1-自顶向下统计
操作方法:在进入dfs之前进行信息统计。
如求链长:树上两个节点必然有且仅有一条路径,我们可以把该路径看成一条链。路径上的边权和为两点的链长。



树上信息统计方式2-自底向上统计
操作方法:在dfs回溯之时进行信息统计。
如求树的节点个数:当前树上共有多少个节点。

子树的概念:
抹除当前根节点以及所有与根节点的连边后,产生的树都是当前根节点的子树。
如当前根节点1的子树有,以2、3、4为根的子树。