一、MVDR算法

1.1 简介

最小方差无失真响应（Mininum Variance Distortionless Response，MVDR）算法最早是J. Capon于1969年提出，用于多维地震阵列传感器的频率-波数分析。随后，Lacoss在1971年将其引入到一维时间序列的分析中。
MVDR算法由于是Capon提出的，所以也将其称为Capon算法。

1.2 原理

根据数字波束形成的原理，得到输入信号 $x(n)$ 经空域滤波后的输出为：
$$y(n)=w^{H}x(n)=w^{H}a(\theta )s(n)（1-1）$$
其中，输入信号 $x(n)$ 为期望、干扰、噪声三种信号的耦合； $a(\theta )$ 为导向矢量。
当一个远场窄带信号 $s(n)$ 入射到 M 个阵元的均匀线阵时，阵列输出信号的平均功率为：
$$P(\theta )=E[|y(n){|}^2]=E[w^{H}x(n)x^H(n)w]=w^{H}Rw（1-2）$$
式(1-2)中 $R=E[x(n)x^H(n)]$ 为接收信号 $x(n)$ 的空间相关矩阵。

假设期望信号从 ${\theta }_0$ 方向入射，阵列接收信号为 $x_0(n)=a({\theta }_0)s(n)$ ，为了使 $x_0(n)$ 通过空域滤波器后无失真，权矢量 $w$ 需满足：
$$w^{H}a({\theta }_0)=1（1-3）$$
选择的加权矢量 $w$ 满足式(1-3)就可以实现对干扰信号以及噪声的抑制，从而使输出信号的平均功率 $P(\theta )$ 最小。由此可以建立目标优化方程为：

采用拉格朗日乘数法对式(1-4)构造代价函数为：
$$J(w)=w^{H}Rw+\lambda (w^{H}a({\theta }_0)-1)（1-5）$$
对式(1-5)关于 $w$ 求梯度，并令其为零，得到：
$$▽J(w)=2Rw-2\lambda a({\theta }_0)=0（1-6）$$
解得： $w=\lambda R^{-1}a({\theta }_0)$ ，将结果代入式(1-3)可得：
$$\lambda =\frac{1}{a^H({\theta }_0)R^{-1}a({\theta }_0)}（1-7）$$
将式(1-7)代入求得的权矢量结果中，可得到 MVDR 波束形成器的最优权向量为：
$$w_{opt}=\frac{R^{-1}a({\theta }_0)}{a^H({\theta }_0)R^{-1}a({\theta }_0)}（1-8）$$
以上就是 MVDR 波束形成求权值的完整过程。当阵列的阵元个数为 $M$ 时，阵列的自由度为 $M-1$，所以 MVDR 波束形成器要求干扰源个数必须小于或等于 $M-1$。
在实际情况中，阵列的接收数据协方差矩阵只能在有限次快拍的情况下，用时间平均对采样数据进行估计得到，即：
$$R^{ˆ}=\frac{1}{N}\sum _{n=1}^{N}x(n)x^H(n)（1-9）$$
其中，$N$ 是采样快拍数， $N$ 值越大，估计矩阵 $R^{ˆ}$ 更接近理想的相关矩阵 $R$。

1.3 特点

1.3.1 优点

（1）高分辨率：MVDR算法能够有效地分辨出多个声源的方向，具有较高的分辨率。这使得它在处理复杂声学环境时能够提供更准确的声源定位信息。

（2）鲁棒性强：MVDR算法对噪声和混响信号具有较强的鲁棒性。在存在噪声和混响的环境中，该算法能够较好地保持对声源方向的估计能力，提高系统的稳定性和可靠性。

（3）计算量相对较小：相较于一些更复杂的算法，MVDR算法的计算量相对较小，这使得它在实时性要求较高的应用场景中具有一定的优势。

（4）干扰抑制能力强：MVDR算法通过最小化其他方向的信号功率，能够有效地抑制多径干扰和噪声，提高信号的质量。这在无线通信、声纳和雷达等领域尤为重要。

1.3.2 缺点

（1）远场假设限制：MVDR算法假设声源位于远场，即声源与麦克风阵列之间的距离远大于阵列的尺寸。这一假设限制了算法在近场声源定位中的应用，因为对于近场声源，算法的定位精度会显著下降。

（2）对导向矢量误差敏感：MVDR算法的性能在很大程度上依赖于导向矢量的准确性。如果导向矢量存在误差，将会对算法的估计结果产生较大影响，降低定位精度。

（3）阵列尺寸限制：MVDR算法的性能与阵列尺寸有关。一般来说，阵列尺寸越大，算法的性能越好。然而，在实际应用中，受到成本和空间等因素的限制，阵列尺寸往往无法做到足够大，这可能会限制算法的性能。

（4）计算复杂度较高：尽管相对于一些更复杂的算法而言，MVDR算法的计算量较小，但在实时性要求极高的应用场景中，其计算复杂度仍然可能成为一个挑战。此外，为了获得更好的性能，可能需要对算法进行进一步的优化和加速。

二、算法应用实例

2.1 信号的频率估计

仿真1：对目标信号的到达角进行估计
设一维均匀线阵的阵元数目为8，其间距为半波长，有3个目标信号的到达角分别为-30°，0°，20°，利用MVDR算法对该目标信号进行到达角估计，计算结果如下图所示。

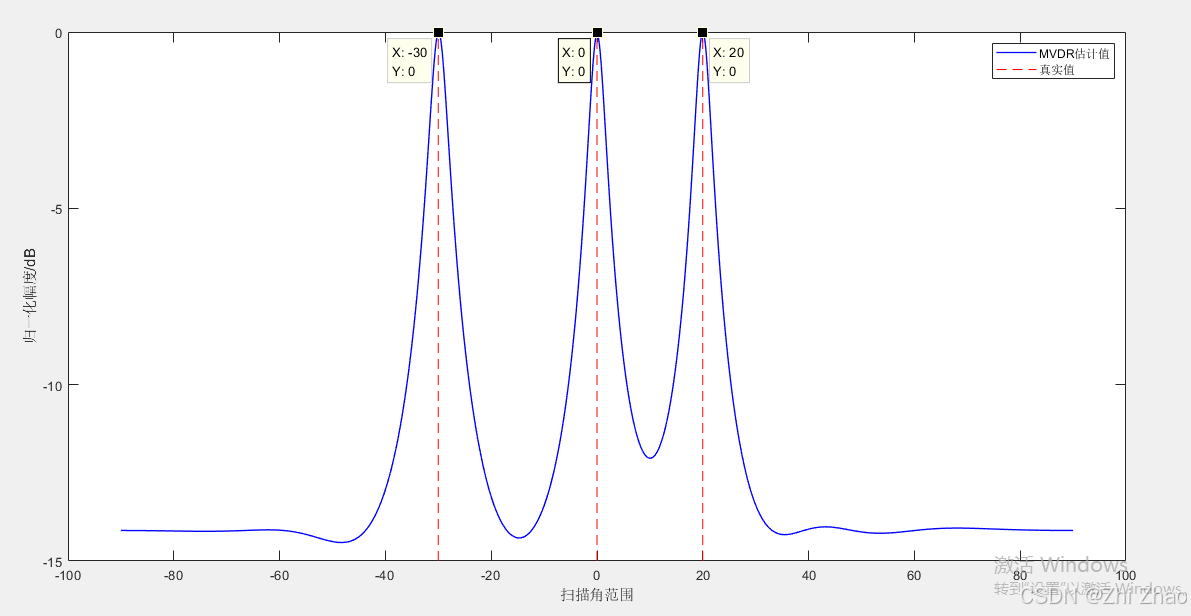
读者可根据自己的需求，设置阵元数、目标信号个数及目标真实角度、信号的信噪比等条件进行实验。

2.2 MATLAB仿真代码

clc;
clear;
close all;

%% MVDR算法估计到达角
d_lambda = 0.5;         % 阵元间距与波长比
Rx_Num = 8;             % 接收天线阵元数

N = 1000;               % 采样快拍数
sigNum = 3;             % 信源数目
theta0 = [-30,0,20];     % 真实来波角度
snr = 10;               % 信噪比

S = randn(sigNum,N)+1j*randn(sigNum,N);     % 远场窄带信号
A = exp(1j*2*pi*d_lambda*sind(theta0).'*(0:Rx_Num-1)).';     % 导向矢量
X = A*S;                            % 接收信号
Y = awgn(X,snr,'measured');         % 添加噪声的接收信号

R = Y*Y'/N;         % 接收数据的协方差矩阵
R_ = inv(R);        % 协方差矩阵的逆矩阵

thetaScan = (-90:0.1:90);       % 扫描角度范围
As = exp(1j*2*pi*d_lambda*sind(thetaScan).'*(0:Rx_Num-1)).';

num = 0;
P = zeros(1,length(thetaScan));     % 谱峰函数初始化
for ii = thetaScan
    num = num+1;
    P(num) = 1/(As(:,num)'*R_*As(:,num));
end
P = 10*log10(abs(P)/max(abs(P)));   % 对谱峰函数进行归一化并取对数
figure;
plot(thetaScan,P,'b','LineWidth',1);xlabel('扫描角范围');ylabel('归一化幅度/dB');hold on
ylim = get(gca,'Ylim');
for jj = 1:sigNum
    % 画出真实波达角的值进行对比
    line([theta0(jj) theta0(jj)],[ylim(1) ylim(2)],'Color','r','LineStyle','--');
    hold on;
end
legend('MVDR估计值','真实值');

三、参考文献

[1] Capon J. High-resolution frequency-wavenumber spectrum analysis[J]. Proc. IEEE, 1969, 57(8): 1408-1418.
[2] Lacoss R T. Data adaptive spectral analysis methods[J]. Geophysics, 1971, 36(8): 661-675.
[3] 胡君丽.数字阵列接收同时多波束技术研究[D].电子科技大学,2019.