近日,中国星坤推出的X0800HI系列线对板连接器,凭借其独特的设计和卓越的性能,引起了业界的广泛关注。

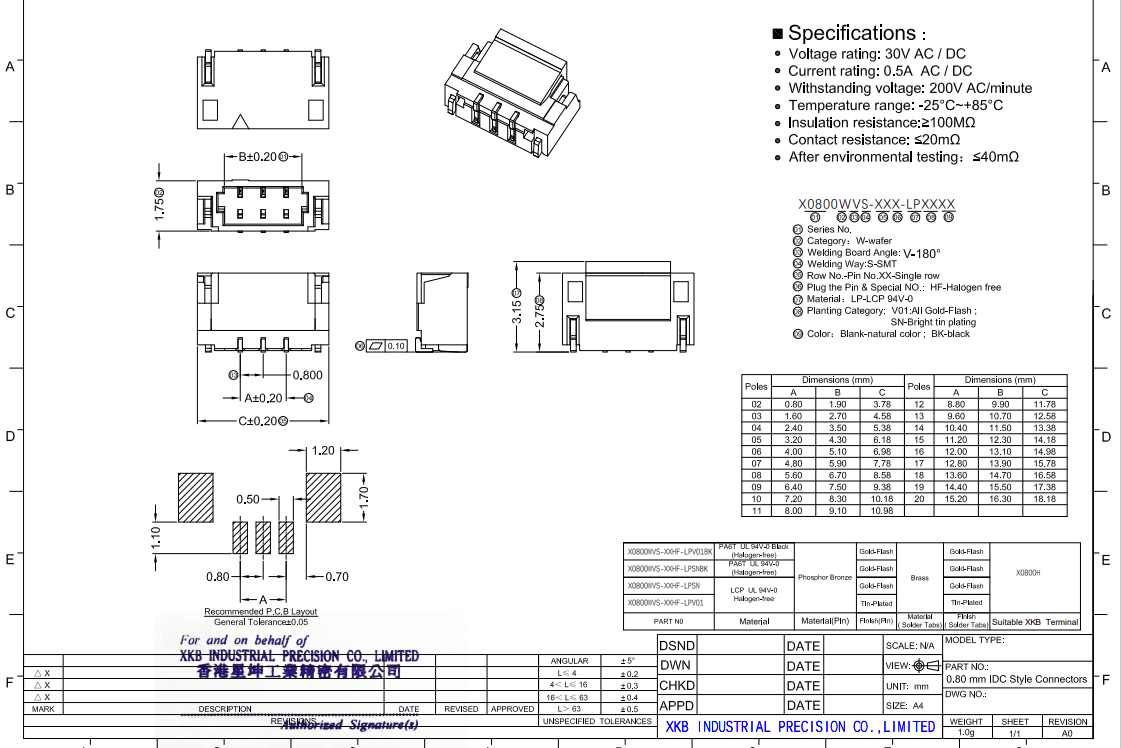
X0800HI系列线对板连接器在极小空间内实现了线对板的W-B连接,这不仅解决了传统连接方式中剥线和焊接的繁琐步骤,还大大简化了安装过程。其压接刺破式线束设计,使得线束可以通过全自动设备进行生产加工,既保证了质量,又提高了生产效率。
在智能家居领域,X0800HI系列连接器因其小巧的体积和高效的连接性能,成为了智能家居设备中不可或缺的组成部分。无论是智能灯泡、智能插座,还是智能摄像头,这些连接器都能帮助设备快速、稳定地连接到电路板,为智能家居的顺畅运行提供了有力保障。
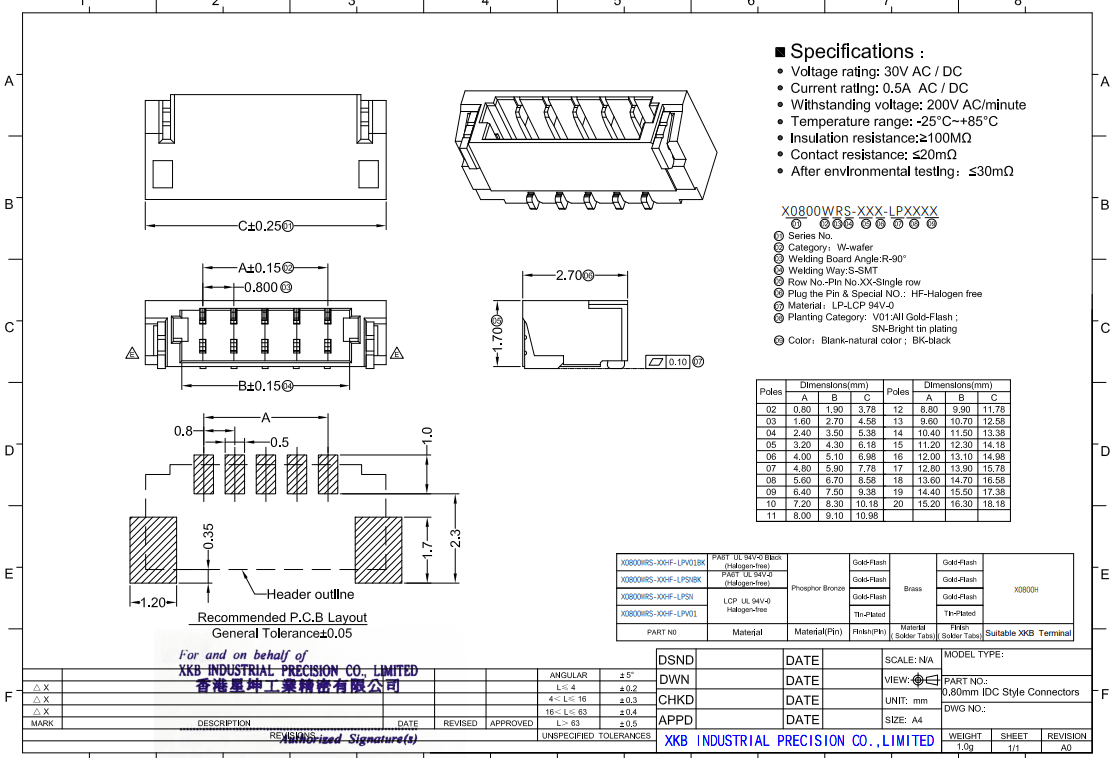
在通讯设备和消费类电子领域,X0800HI系列连接器同样展现出其独特的优势。随着5G技术的普及和消费者对电子产品性能要求的提高,传统连接器的性能和便捷性已难以满足市场需求。而X0800HI系列连接器不仅具有更高的连接密度和更小的占用空间,还能适应超细线的连接需求,为通讯设备和消费类电子产品的升级换代提供了有力支持。

值得一提的是,与传统1.0mm间距的X0800连接器相比,X0800HI系列连接器在电路板上的占用空间减少了34%(侧入式)。这意味着在相同的电路板面积下,可以安装更多的连接器,进一步提高了电路板的集成度和可靠性。

中国星坤推出的X0800HI系列线对板连接器凭借其独特的设计和卓越的性能,在智能家居、通讯设备、消费类电子等领域展现出广泛的应用前景。连接器作为电子设备中不可或缺的部件,其性能与便利性直接影响着产品的整体表现。我们有理由相信,该款连接器将成为未来电子产品中不可或缺的重要组件。