前言
欢迎关注个人主页:逸狼
创造不易,可以点点赞吗~
如有错误,欢迎指出~
判断是否是相同的树
oj链接
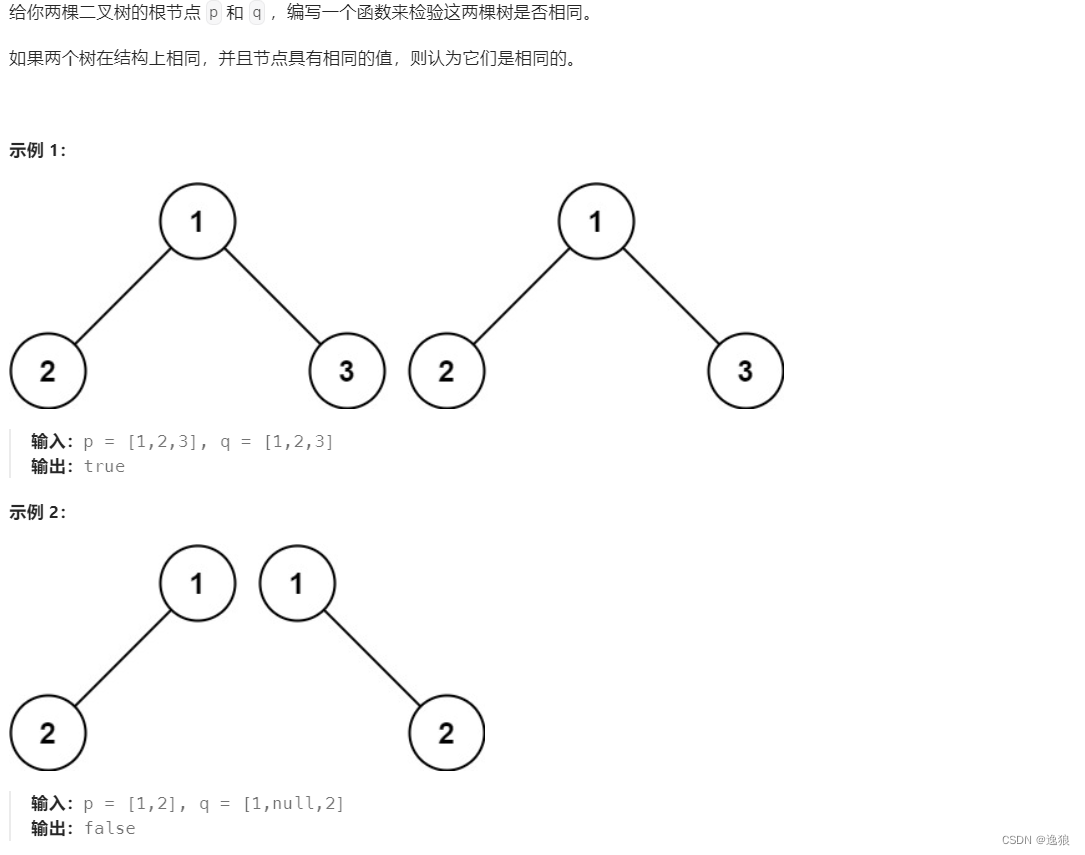
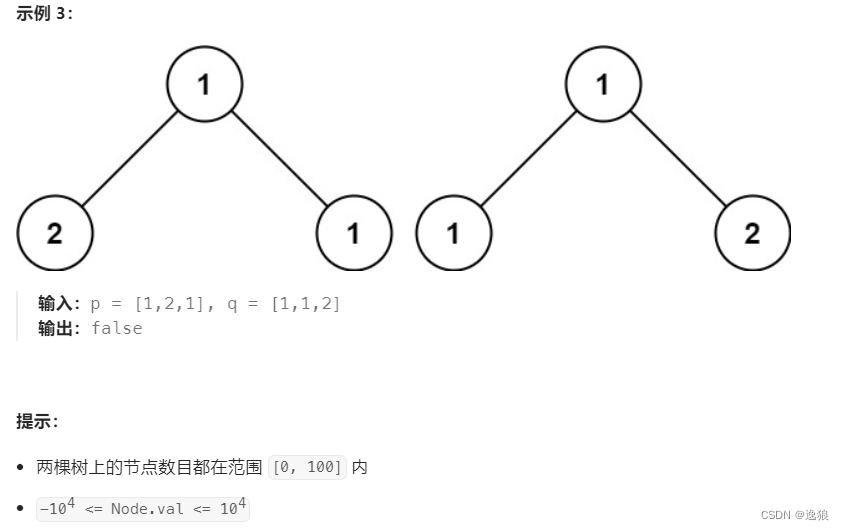
要判断树是否一样,要满足3个条件
- 根的 结构 和 值 一样
- 左子树的结构和值一样
- 右子树的结构和值一样
所以就可以总结以下思路:
- 一个为空,一个不为空--》一定不相同
- 两个都为空--》 相同
- 都不为空 ,但值不一样--》一定不相同
- 最后递归判断 左子树和右子树都要相同--》两棵树相同
其中该题的时间复杂度为O(min(m,n)),也就是取m和n中最小值(假设p的节点数为m个,q的节点数为n个)
public boolean isSameTree(TreeNode p, TreeNode q) {
//一个为空,一个不为空
if(p!=null&&q==null||p==null&&q!=null){
return false;
}
//此时要么两个都为空,要么都不为空
if(p==null&&q==null){
return true;
}
//都不为空
if(p.val!=q.val){
return false;
}
//此时两个都不为空,val值也一样,说明根节点相同
//判断左右树是否相同
return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
另一棵树的子树
oj链接
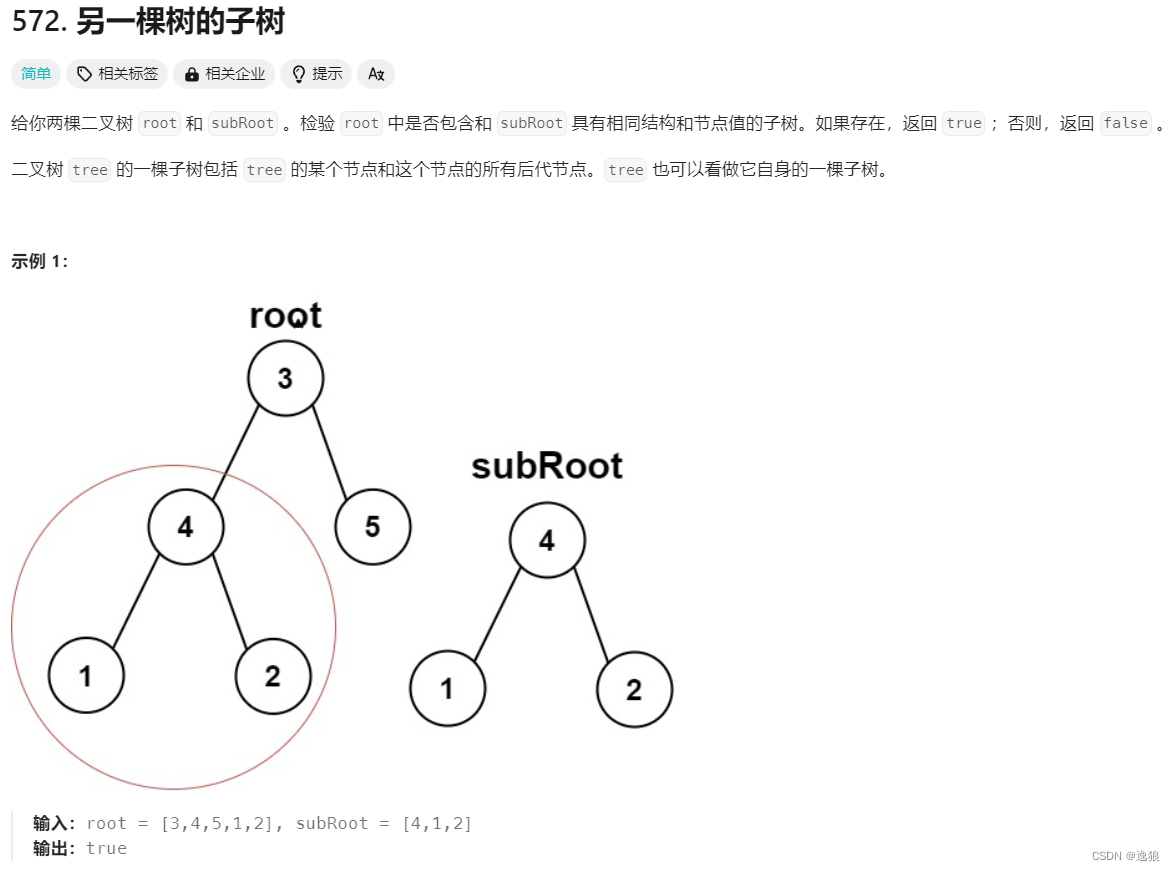
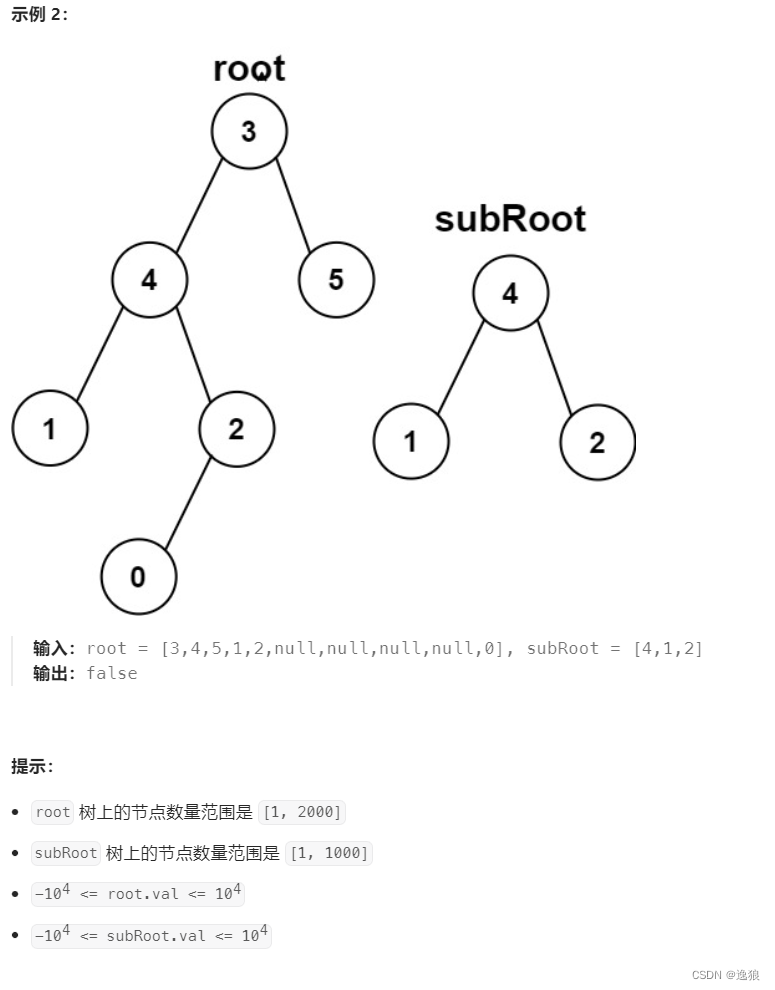
当两颗树相同时,也属于子树
所以步骤如下
- 判断是不是两颗相同的树
- 若不是,有可能是左子树的子树
- 也有可能是右子树的子树
其中该题的时间复杂度为m*n (假设root有n个节点,subRoot有m个节点),原因是root的每一个节点都要和subRoot的节点比对
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
//因为root要递归,递归到后面root可能为空
if(root==null){
return false;
}
//两颗树相同时,成立
if(isSameTree(root,subRoot)){
return true;
}
//判断root的左子树和subRoot
if(isSubtree(root.left,subRoot)){
return true;
}
//判断root的右子树和subRoot
if(isSubtree(root.right,subRoot)){
return true;
}
return false;
}
public boolean isSameTree(TreeNode p, TreeNode q) {
//一个为空,一个不为空
if(p!=null&&q==null||p==null&&q!=null){
return false;
}
//此时要么两个都为空,要么都不为空
if(p==null&&q==null){
return true;
}
//都不为空
if(p.val!=q.val){
return false;
}
//此时两个都不为空,val值也一样,说明根节点相同
//判断左右树是否相同
return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
}翻转二叉树
oj链接
让root的左节点和右节点交换,再递归遍历root.left和root.right使左子树和右子树都翻转。
代码优化:若只有一个根节点(左右子树都为空),直接返回;减少了递归和交换的次数
public TreeNode invertTree(TreeNode root) {
if(root==null){
return null;
}
//代码优化部分******减少一些递归和交换的次数
if(root.left==null&&root.right==null){
return root;
}
// ******
TreeNode ret=root.left;
root.left=root.right;
root.right=ret;
invertTree(root.left);
invertTree(root.right);
return root;
}判断一颗二叉树是否是平衡二叉树
平衡二叉树 是指该树所有节点的左右子树的深度相差不超过 1
oj链接
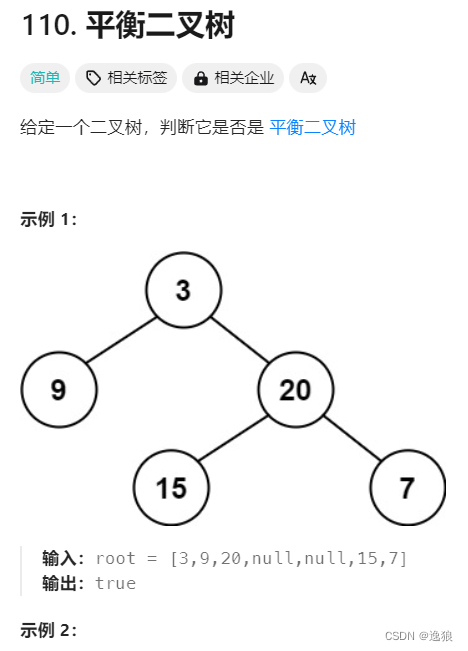
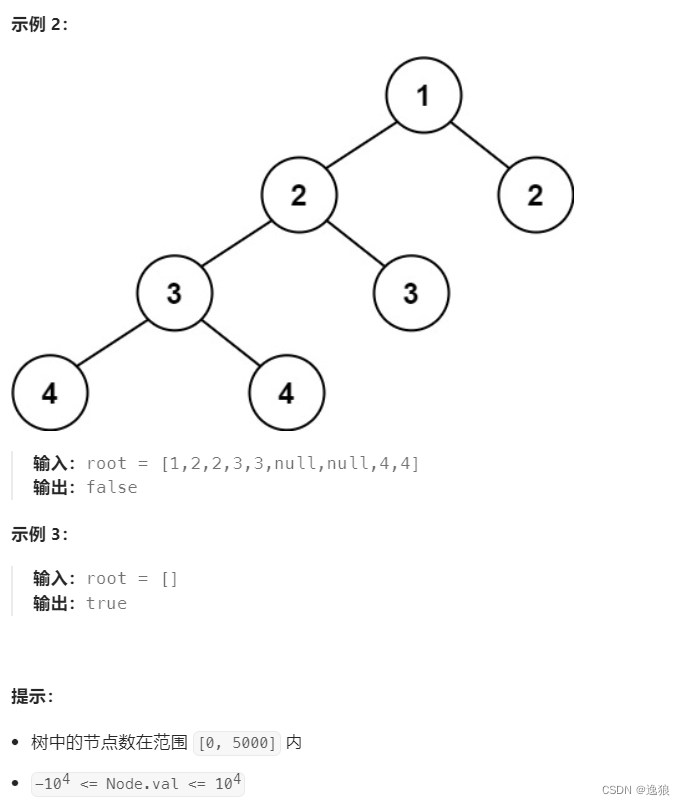
判断步骤:
当前root的 左子树 和 右子树的高度差<=1
同时满足root的左 右子树平衡
其中该题的时间复杂度为O(n^2)
public boolean isBalanced(TreeNode root) {
if(root==null) return true;
int leftH=maxDepth(root.left);
int rightH=maxDepth(root.right);
return Math.abs(leftH-rightH)<=1
&&isBalanced(root.left)
&&isBalanced(root.right);
}
public int maxDepth(TreeNode root){
if(root==null){
return 0;
}
int leftH=maxDepth(root.left);
int rightH=maxDepth(root.right);
return leftH>rightH?leftH+1:rightH+1;
}代码优化,使得时间复杂度变为O(n)
public boolean isBalanced(TreeNode root) {
if(root==null) return true;
return maxDepth(root)>=1;
}
public int maxDepth(TreeNode root){
if(root==null){
return 0;
}
int leftH=maxDepth(root.left);
if(leftH<0){
return -1;
}
int rightH=maxDepth(root.right);
if(rightH<0){
return -1;
}
if(Math.abs(leftH-rightH)<=1){
return leftH>rightH?leftH+1:rightH+1;
}else{
return -1;
}
}第三种写法
public boolean isBalanced(TreeNode root) {
if(root==null) return true;
return maxDepth(root)>=1;
}
public int maxDepth(TreeNode root){
if(root==null){
return 0;
}
int leftH=maxDepth(root.left);
// if(leftH<0){
// return -1;
// }
int rightH=maxDepth(root.right);
// if(rightH<0){
// return -1;
// }
if(leftH>=0&&rightH>=0
&&Math.abs(leftH-rightH)<=1){
return Math.max(leftH,rightH)+ 1;
}else{
return -1;
}
}