FFT
空间域中矩阵的卷积算子,实际等于频率域中两个矩阵元素相乘。但卷积的方向是相反的。
通常情况下,feature的尺寸要比卷积的尺寸大很多,如果对两者进行快速傅里叶变换的话,得出来的两个矩阵大小不一样,不能进行对应位置相乘。
为了可以让他们对应位置相乘,必须要对卷积核进行扩充,将其扩充到feature尺寸大小相同。也正是扩充过程,限制了方法的使用,只有当feature尺寸和卷积核尺寸大小差不多的时候,才会采用这种方法。
通常有三种卷积方式:full、same、valid
full卷积方式:会先对图像的四周进行补0,补零的行数(列数)为卷积核宽度(高度)-1,最终卷积出来的结果一定会比原图像大的

same卷积方式:这种卷积方式的结果大小一定会与原图像一样,通常补零的个数为向下取整
卷积核大小为n/2

valid卷积方式:不会对原图进行补零操作,所以会导致原图像大小变小

现在来分析,如果使用FFT来进行快速卷积,怎么补零
假设,我们输入的图像和卷积核分别如下


如果用full方式进行卷积,补零结果如下

这是因为,在用full方式进行卷积的时候,原图8x7大小,会变成10x9的大小,所以我们要把原图填充成上述样子。同理,我们需要把卷积核进行填充至10x9的大小

我们需要先对其进行水平翻转和垂直翻转,再进行卷积运算
所以对feature和核填充0后,还要再进行水平翻转和垂直翻转
def fftConvt(img,ker):
//第一步:对图像进行填充
img_padding = np.zeros(shape = [len(img)+len(ker)-1],[len(img)+len(ker)-1])
img_padding[(len(ker)-1:len(ker)-1+len(img)),len(ker[0])-1:len(ker[0])-1+len(img)]=img
ker = np.flip(ker,axis=0)
ker = np.flip(ker,axis=1)
//第二步,对卷积核进行填充
ker_padding = np.zeros(shape = img_padding.shape)
ker_padding[:len(ker),:len(ker[0])]=ker
img_padding_fft2=np.fft.fft2(img_padding)
ker_padding_fft2=np.fft.fft2(ker_padding)
img_fft2=img_padding_fft2*ker_padding_fft2
return np.real(np.fft.fft2(img_fft2))
img2col
将卷积运算转换为矩阵乘法运算。

输入数据是一个三通道的features

我们有两个卷积核,每个卷积核有三个子核

如何把卷积转换为矩阵乘法呢?
传统卷积中,我们采用滑动窗口进行加权求和。将每个滑块所形成的字矩阵拉直,我们拿出第一个features进行拉直

拿出第一个卷积核中的子矩阵

现在移动滑动窗口,逐一进行拉直

然后形成了四个向量,将其堆叠起来,形成一个新的矩阵

再将卷积核拉直

现在,就可以用之前形成的矩阵和拉直的卷积核进行矩阵乘法

做乘法之后,每个窗口会得到一个列向量,这个列向量就是每个窗口加权平均值,即卷积值,3*3矩阵做2*2卷积,输出是2*2,将列向量reshape,即可得到最终结果。

对于多通道,我们将三个通道生成的矩阵堆叠在一起

每个卷积核的子矩阵给拉直,然后再堆叠到一起

最后实现两者的乘积,即可得到卷积结果
def img2col(img,ker):
ker_width=len(ker[0])
ker_height=len(ker)
transform=np.empty(shape=((len(img[0]) - ker_width)*(len(img) - ker_height), ker_width*ker_height))
cur=0
for y in range(0,len(img)-ker_height):
for x in range(0, len(img[0]) - ker_width):
data=img[y:y+ker_height,x:x+ker_width].reshape(1,9)
transform[cur,:]=data
cur=cur+1
return np.dot(transform,ker.reshape(-1,1)).reshape(len(img)-ker_height,-1)
Winograd 需要仔细阅读
Winograd算法出自CVPR 2016的一篇 paper:Fast Algorithms for Convolutional Neural Networks。,这个算法可以用来加速卷积运算,目前有很多框架如NCNN、NNPACK等,对于卷积层都采用了Winograd快速卷积算法。
卷积神经网络中的Winograd快速卷积算法
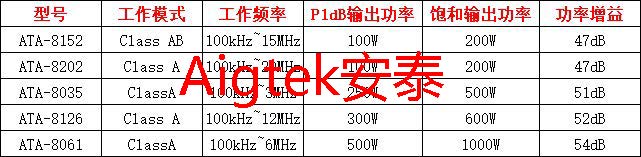
- Winograd算法通过减少乘法次数来实现提速,但是加法的数量会相应增加,同时需要额外的transform计算以及存储transform矩阵,随着卷积核和tile的尺寸增大,就需要考虑加法、transform和存储的代价,而且tile越大,transform矩阵越大,计算精度的损失会进一步增加,所以一般Winograd只适用于较小的卷积核和tile(对大尺寸的卷积核,可使用FFT加速),在目前流行的网络中,小尺寸卷积核是主流,典型实现如F(6×6,3×3)𝐹(6×6,3×3)、F(4×4,3×3)𝐹(4×4,3×3)、F(2×2,3×3)𝐹(2×2,3×3)等,可参见NCNN、FeatherCNN、ARM-ComputeLibrary等源码实现。
- 就卷积而言,Winograd算法和FFT类似,都是先通过线性变换将input和filter映射到新的空间,在那个空间里简单运算后,再映射回原空间。
- 与im2col+GEMM+col2im相比,winograd在划分时使用了更大的tile,就划分方式而言,F(1×1,r×r)𝐹(1×1,𝑟×𝑟)与im2col相同。
def Winograd(img,ker):
U = G.dot(ker).dot(G.T)
res=np.empty(shape=[98,98])
for y in range(0,len(img)-8,6):
for x in range(0, len(img[0])-8,6):
tile=img[y:y+8,x:x+8]
V=BT.dot(tile.T).dot(BT.T)
res[y:y+6,x:x+6]=AT.dot(U*V).dot(AT.T).T
return res