假设有这么个正整数n，要求输出1到n的所有排列？
 
输入：3
输出：123，132，213，231，312，321

一、无脑循环求解？

拿到这个问题，当然我的第一个想法就是 for 循环，比如这样：

for(int i = 1; i < n+1; i++){
	for(int j = 1; j < n+1; j++){
		for(int k = 1; k < n+1; k++){
			……从此陷入无尽的循环
		}
	}
}

可是，问题大了，循环到底有多少个？n 个？

又或者是 while 循环来控制循环次数：

while(i < n){
	for(int j = 1; j < n+1; j++){
		……就这样又陷入循环
	}
	i++;
}

其实，如果了解回溯算法，也不至于拿个 for 循环来为难自己，下面就来分析一下这个问题。

二、全排列的个数

首先，关于这个全排列问题，很容易就能得到问题的答案个数为 n！个：

当 n = 2 时，全排列的个数为 2 个：

[1,2]、[2,1]

当 n = 3 时，全排列的个数为 3*2 ，即 6 个：

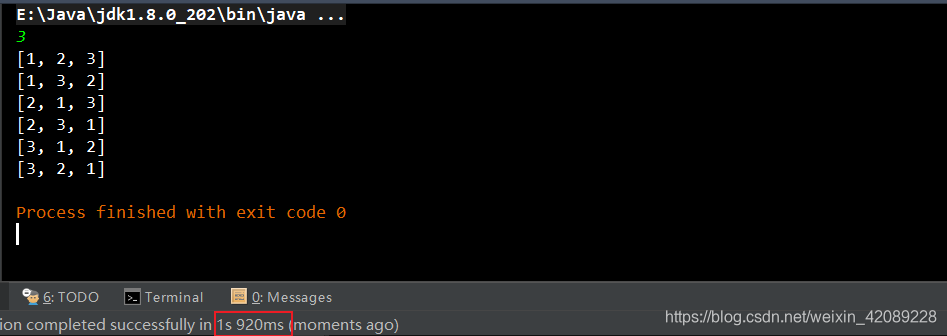
[1,2,3]、[1,3,2]、[2,1,3]、[2,3,1]、[3,1,2]、[3,2,1]

当 n = 4 时，全片列的个数为 4*3*2 ，即 24 个

[1, 2, 3, 4]、[1, 2, 4, 3]、[1, 3, 2, 4]、[1, 3, 4, 2]、[1, 4, 2, 3]、[1, 4, 3, 2]、
[2, 1, 3, 4]、[2, 1, 4, 3]、[2, 3, 1, 4]、[2, 3, 4, 1]、[2, 4, 1, 3]、[2, 4, 3, 1]、
[3, 1, 2, 4]、[3, 1, 4, 2]、[3, 2, 1, 4]、[3, 2, 4, 1]、[3, 4, 1, 2]、[3, 4, 2, 1]、
[4, 1, 2, 3]、[4, 1, 3, 2]、[4, 2, 1, 3]、[4, 2, 3, 1]、[4, 3, 1, 2]、[4, 3, 2, 1]

很容易推出 n 个数字时，全排列的个数为 n! 个。

三、回溯算法解题

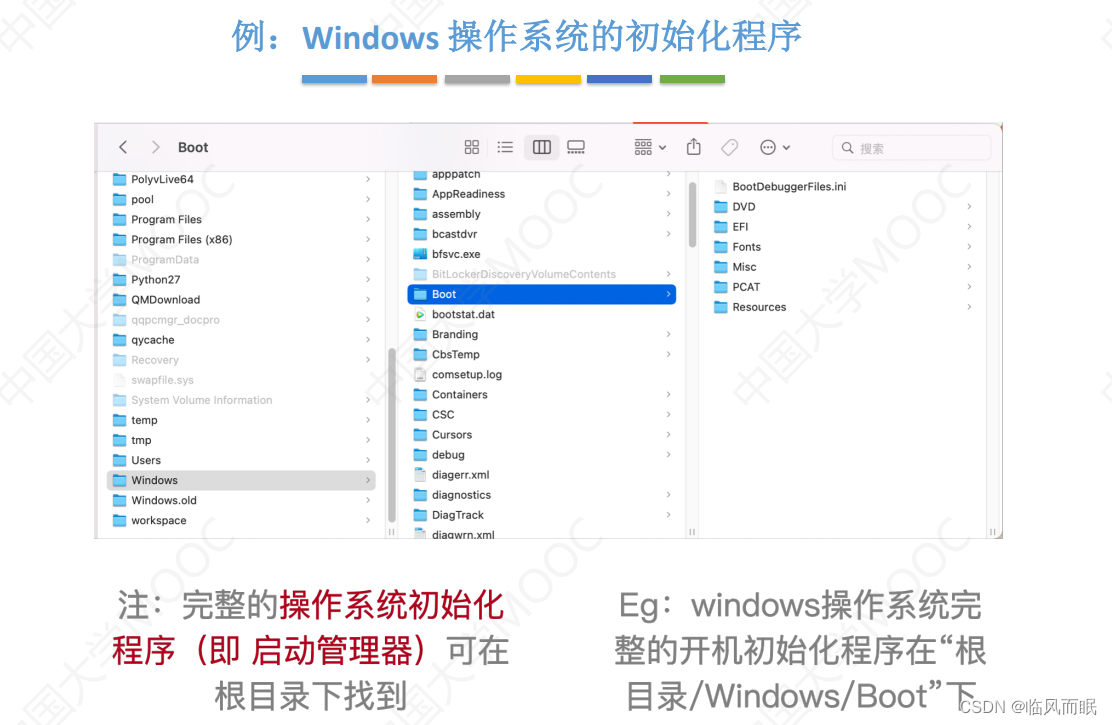
接下来就利用回溯算法来解决这个问题，还是比较简单的。首先，我们需要构建全排列的解空间。同样这里先研究规模较小的问题，假设 n 为 3 时的解空间：

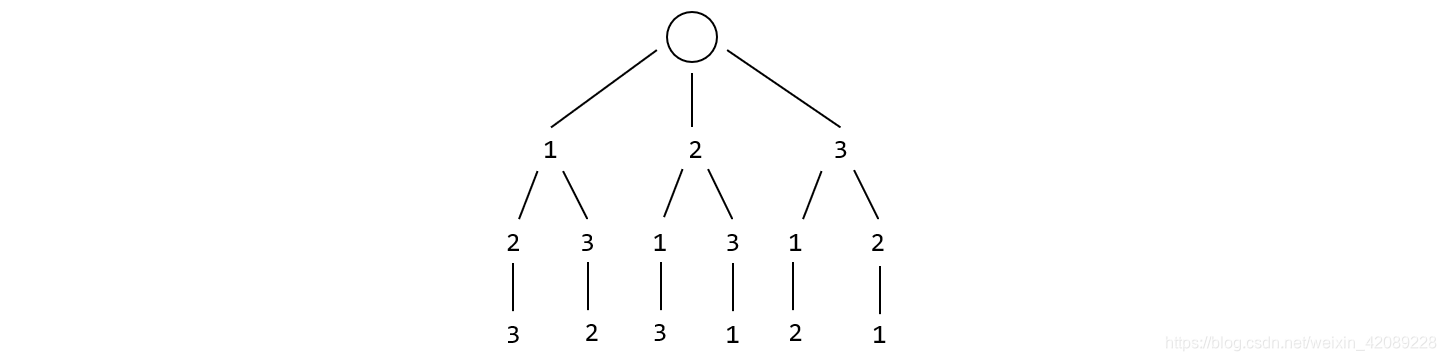
回溯算法的解空间就是一颗多叉树，通常根节点为空。这这颗多叉树中，叶子结点被称为不可扩展的结点，非叶子结点称为可扩展结点。

接下来，就需要通过深度遍历来遍历这颗多叉树，每次遍历至叶子结点，就可以得到一个相应的解。

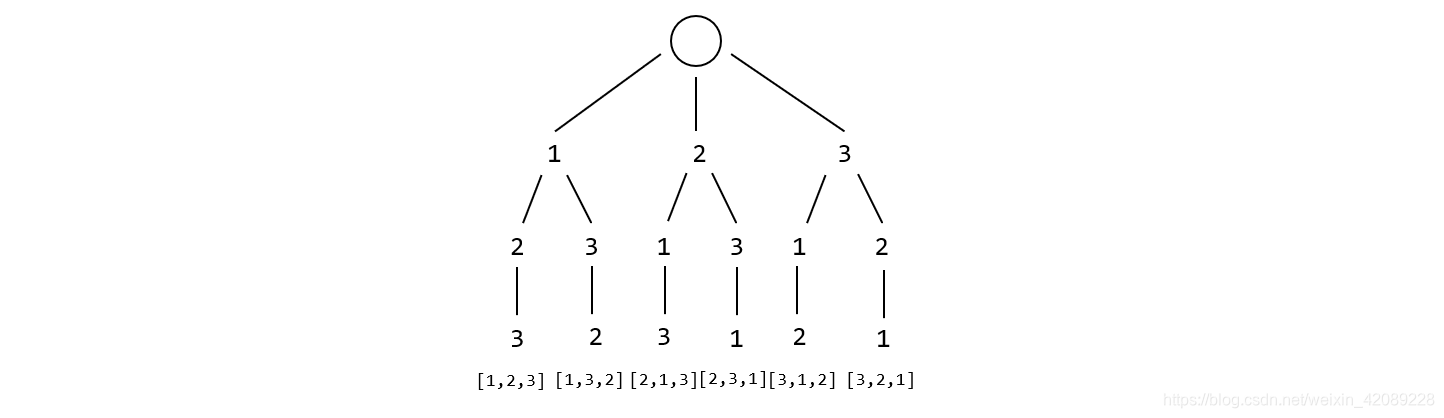
回溯就发生在遍历的过程中，当遇到不可扩展的结点时，就需要回溯到树的上一层，继续遍历其他可扩展结点。

接下来就可以用代码来实现了，主要有两种方式来实现回溯算法：

1、递归实现回溯算法

  递归实现思路：函数自调，通过自调函数来不断向树的深处进行遍历；而通过 for 循环，来找到合适的结点，并暂存在结果集中。递归终止时，即获得一个完整的结果！

/**
 * 
 * @param t 	起始层数，初始值为 1
 * @param n		数的个数，也是树的最后一层
 * @param ls	结果集
 */
public static void backTrack(int t, int n, ArrayList<Integer> ls) {
		if(t > n) {
			System.out.println(ls.toString());
		}else {
			for(int i = 1; i < n+1; i++) {
				if(ls.contains(i))
					continue;
				else
					ls.add(i);
				backTrack(t+1, n, ls);
				ls.remove(t-1);
			}

		}
}

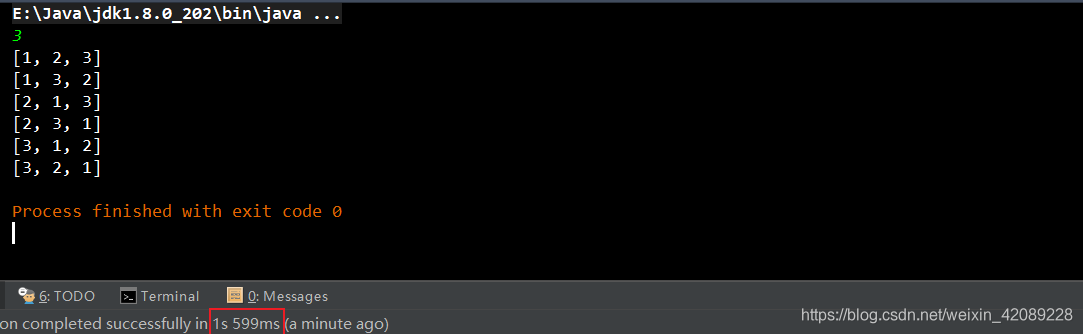
下面是递归调用的抽象过程：

观察这个过程，你会发现递归对于回溯算法是具有天生的优势的，或者说递归就是一个不断回溯的过程；而迭代实现回溯算法是比较难以理解的。

2、迭代实现回溯算法

  递归实现思路：使用迭代来实现回溯，就像一头扎进死胡同，然后再一步一步回退，回退之后再扎进死胡同。直到回退到胡同外，即退出整个回溯过程。

/**
 * @param n 	数的个数
 * @param ls	结果集
 */
public static void iterativeBacktrack(int n, ArrayList<Integer> ls) {
		int t = 1;
		int left = 1;
		while(t > 0) {
			if(left <= n) {
				for(int i = left; i <= n; i++) {
					if(ls.contains(i)) {
						continue;
					}else {
						if(ls.size() == t){
							ls.set(t-1, i);
						}else{
							ls.add(t-1, i);
						}
						i = 0;
					}
					if(t == n) {
						System.out.println(ls.toString());
					}else {
						t++;
						i=0;
					}
				}
			}
			if (t > 0){
				ls.remove(t-1);
			}
			t--;
			if(t > 0)
				left = ls.get(t-1);
		}
}

---

其实回溯算法还有最后一步，通过约束条件和边界控制来剪去多余的枝干，以提升回溯算法的效率。 这里，就不进行剪枝了……