趣味三角——第6章——两个几何定理

第6章两个几何定理

It is the glory of geometry that from so few principles,

fetched from without, it is able to accomplish so much.

(几何学的荣耀在于，仅从几个原理出发，外求于无物，但却能够完成如此非凡的壮举。)

——Isaac Newton

欧几里德(Euclid)<<几何原理>>(Elements)第三册的命题(proposition) 20 说：

在一个圆中，当圆心角与圆周角的圆周(即角所对应的圆上的圆弧段)相同时，圆心角是圆周角的两倍。[1]

用更通俗的话言来表述，这个命题指的是,一个内接(inscribed)圆中的角(即，顶角在圆周上的角，不妨称为“圆周角”)等于正对向是同一条弦的圆心角的一半(图28)。

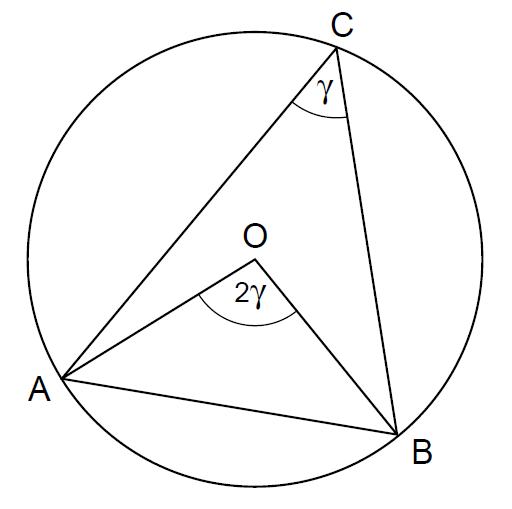
----------图28 Euclid几何原理第三册的命题命题20-------------------------

这个定理的两个推论(corollaries)紧随其后：(1) 在一个已知圆中，所有正对向为同一条弦的内接圆周角相等(这是Euclid的第21个命题；见图29)；(2) 所有正对向为同一条直径的内接圆周角都是直角(见图30)。据说最后一个结果已经被泰勒斯(Thales)证明了(尽管巴比伦人在他之前一千年就已经知道了)并且可能是有史以来最早被证明的定理之一。

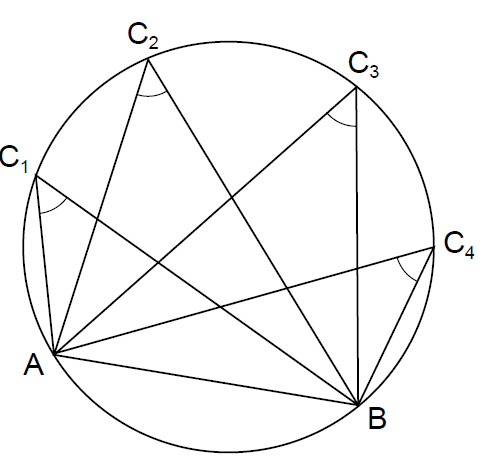
----------图29 Euclid几何原理第三册的命题命题21-------------------------

----------图30所有正对向为同一条直径的内接圆周角都是直角------------------

这个简单的定理及其两个推论是三角函数信息的瑰宝(treasure trove)，我们将在本书中多次使用它。让我们在这里用它来证明正弦定理。图31展示了一个圆内接三角形ABC，O为圆心，半径为r。

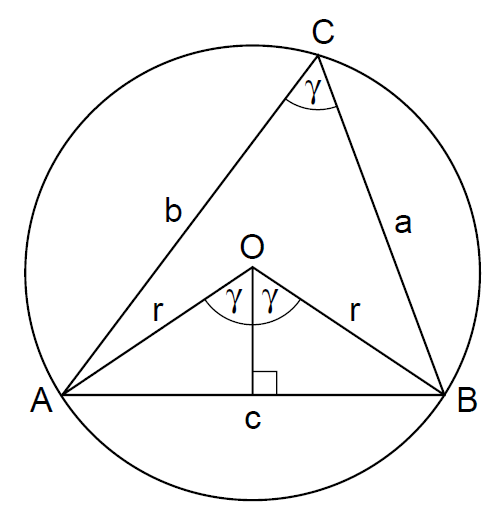
-------------------------------图31 正弦法则锐角案例------------------

我们有，∠AOB = 2∠ACB = 2γ。从O到AB画一条垂直平分线。则sin(γ) = (c/2)/ γ，因此，c/ sin(γ) = 2r = 常量。因此，比率c/ sin(γ)是一个常量(即，不管c和γ如何改变，其比值保持定值)，我们有

$\frac{a}{sin\alpha }=\frac{b}{sin\beta }=\frac{c}{sin\gamma }$ -----------------------------------------(1)

这个证明不仅是一个简单的模型，它还给出了完整形式的正弦定律；更通用的证明，基于将一个三角形分成两个直角三角形，完全忽略了关于2r的陈述。

在图31中，γ是一个锐角(acute),这意味着圆心位于三角形内。假如γ是一个钝角(obtuse)(图32)，则圆心在三角形外，因此，(γ对向的)圆弧AB大于半圆周。

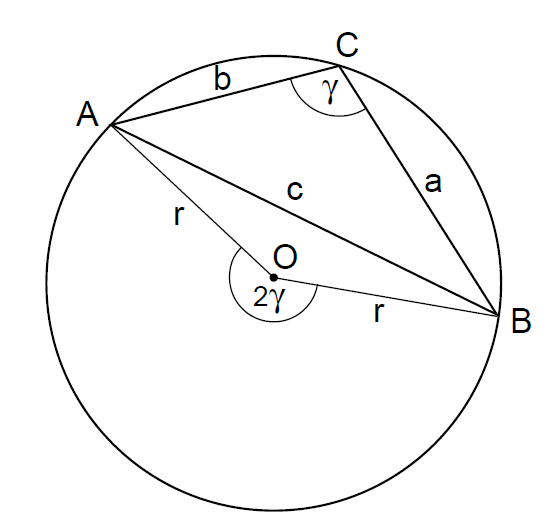
-------------------------------图32 正弦法则钝角案例-------------------------------------------

因此，以O为圆心的圆心角AOB为γ’ = 360°- 2γ 。再次，从O到AB画一条垂直平分线：我们有，sin(γ’/2) = (c/2)/ γ。但是，sin(γ’/2) = sin(180°- γ) = sin(γ)。因此，我们还是得到c/ sin(γ) = 2r ,如前一样。

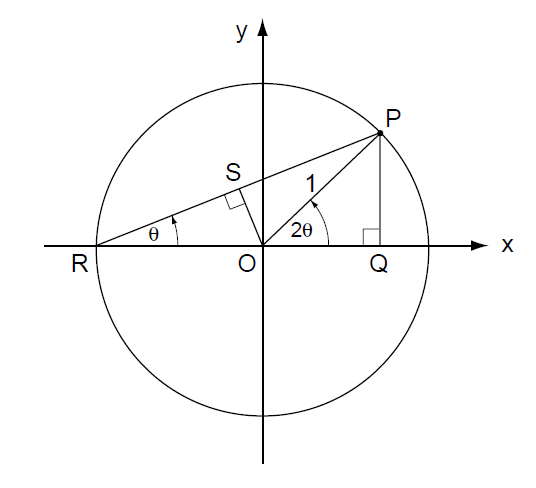
------------------------------------图33 倍角公式的几何证明--------------------------------------------

从我们的定理，我们还可以获得更多的信息。图33展示了一个单位圆及其上的一点P。我们令OP与正向x轴之间的夹角为2θ。则∠ORP = θ ,其中，其中R的坐标点为(-1,0)。对∠ORP应用正弦法则，我们得到RP/sin(180°- 2θ) = OP/sinθ 。但是，sin(180°- 2θ) = sin(2θ)，并且OP = 1,因此，RP/sin(2θ) = 1/sinθ ,从此，我们得到

sin(2θ) = RP sinθ -------------------------------------(2)

现在从O点向RP作垂直平分线OS ；在直角三角形ORS中, 我们有cosθ = RS/RO = (RP/2)/RO = (RP/2)，因此，RP = 2cosθ , 将这个等式代回到公式(2)，我们得到

sin2θ = 2sinθcosθ-------------------------------------(3)

这就是正弦函数的倍角公式。再用同样的作垂线法，从P点向x轴作垂线PQ, 我们有

$cos2\theta = OQ = RQ - RO = RPcos\theta -1 = (2 cos\theta ) cos\theta -1 = 2cos^{2}\theta -1------(4)$

这就是余弦函数的倍角公式。最后，在证明了倍角公式后，我们只需将2θ替换为Φ即可推导出相应的半角公式。

让我们暂时回到正弦定理的证明。由于任意三个不共线的(noncollinear)点唯一确定一个圆，因此每个三角形都可以恰好内接(inscribed)在一个圆中。实际上，我们可以将三角形的角视为内接角，将边视为该圆中的弦。因此，正弦定理实际上是一个关于圆的定理。如果我们让内接圆的直径(diameter)为单位1并将这个圆称为“单位圆(unit circle)”，那么正弦定律简单地说就是

a = sinα ，b = sinβ ，c = sinγ ，

即，“在单位圆中, 内接三角形的每一边都等于边所对应角的正弦值。”(见图34) 事实上，我们可以将一个角的正弦“定义”为它在单位圆中所对向的弦的长度，这个定义与将正弦定义为直角三角形两条边之比的传统定义一样好。(事实上，它的优点是角度可以在0°到 180°度之间变化——是直角三角形范围的两倍。) 正如我们在第2章中看到的，Ptolemy在他的弦表中使用的正是对正弦函数的这种解释。

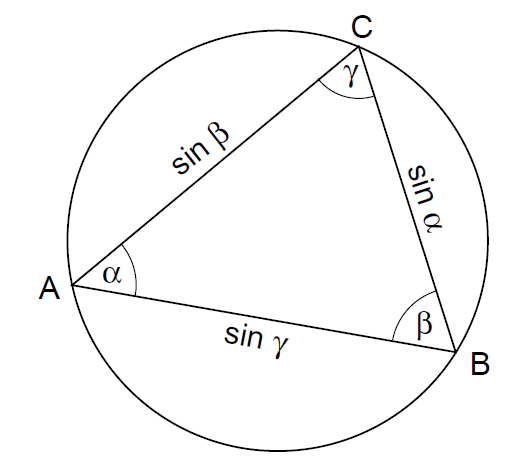
--------------------图34 单位圆中的正弦定律---------------------------------

在Ptolemy的<<天文学大成>>( Almagest)中，我们发现如下的命题，我们称其为Ptolemy定理：[2]

“The rectangle contained by the diagonals of any quadrilateral inscribed in a circle is equal to the sum of the rectangles contained by the pairs of opposite sides”(任何内接于圆的四边形的对角线所包含的矩形等于一对相对边所包含的矩形之和)。[3]

这个神秘的(cryptic)声明是什么意思呢？首先，希腊人将数字解释为线段的长度，将两个数字的乘积解释为以给定数字为边长的矩形的面积。因此，“对角线所包含的矩形”是指边为内接四边形的对角线的矩形的面积，“由一对相对边所包含的矩形”也有类似的解释。简而言之，“包含于……的矩形(a rectangle contained by)”仅表示“……的乘积”。 Ptolemy定理可以表述如下：在一个内接于圆的四边形中，对角线的乘积等于相对边的乘积之和。参见图35。这指的是

AC.BD = AB.CD + BC.DA----------------------(5)

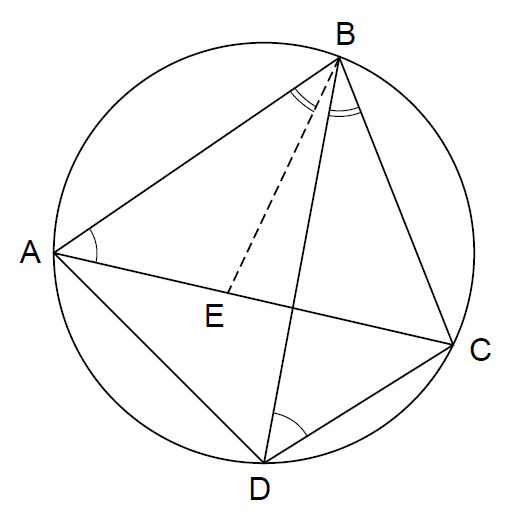
--------------------图35 Ptolemy定理---------------------------------

因为这个定理并不像几何原理中的定理那样广为人知，这里，我们给出Ptolemy的证明方法: 用一条边，比如说AB，作为起始边，我们构造一个角ABE等于DBC。现在，角CAB和角CDB也是相等的，因为它们有相同的对向弦BC。因此，三角形ABE和DBC是相似三角形，具有两对相等的角(译注：实际上是三对相等的角)。因此，AE/AB = DC/DB，从这个等式，我们得到

AE. DB = AB.DC----------------------(6)

假如我们现在将角EBD加到等式∠ABE = ∠DBC两边，我们得到∠ABD = ∠EBC。但是角BDA和角BCE也是相等的，因为它们具有共同的弦AB。因此，三角形ABD和三角形EBC是相似三角形，因此，AD/DB = EC/CB ，所以有

EC. DB = AD.CB----------------------(7)

最后，将等式(6)和(7)相加，我们有(AE + EC). DB = AB.DC + AD.CB ；用AC替换掉AE + EC , 我们得到所求的结果(注意，边是无向线程(非向量),因此，BD = DB , 等等)。

假如我们令四边形ABCD为矩形(图36)，则所有四个角构成直角，此外，AB = CD，BC = DA，以及AC = BD，等式(5)则表明的是

$(AC)^{2} = (AB)^{2}+(BC)^{2}--------(8)$

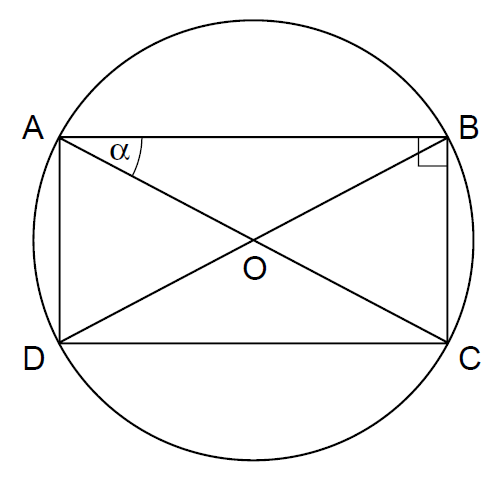
--------------------图36 Ptolemy定理---------------------------------

这正是毕达哥拉斯定理(Pythagorean Theorem，即勾股定理)! 这个最著名的数学定理的证明出现在Elisha Scott Loomis 的经典著作中<<The Pythagorean Proposition>>(毕达哥拉斯命题)256个证明中的第66个中。[4]

Ptolemy定理的三角学意义是什么呢？对于特殊案例ABCD为矩形的情况，AC是我们的单位园中的直径，因此，AC = 1。此外，使用α表示角BAC，我们有AB = cosα ，BC = sinα 。则，代入等式(8)，则成了

$1 = cos^{2}\alpha +sin^{2}\alpha$

这就是勾股定理的等价形式。但是，还能导出更多的东西。令ABCD为任意四边形，其中一条对象线，比如说对角线AC ,使之与直径重合(coincides)(见图37)。则∠ABC和∠ADC是直角。令∠BAC = α, ∠CAD = β。则，我们有BC = sinα, AB = cosα, CD = sinβ, AD = cosβ,以及BD = sin(α+β),因此，通过Ptolemy定理得到

1.sin(α+β) = sinα.cosβ + cosα.sinβ

这是正弦函数的加法公式！

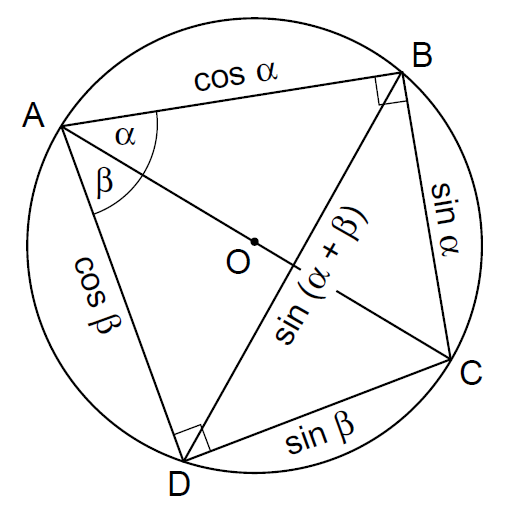
------------------图37 sin(α+β) = sinα.cosβ + cosα.sinβ的几何证明----------

差的公式sin(α-β) = sinα.cosβ - cosα.sinβ同样可以相同的方式获得，考虑一个四边形，其中的一条边，比如说AD ，使之与直径重合(见图38))。

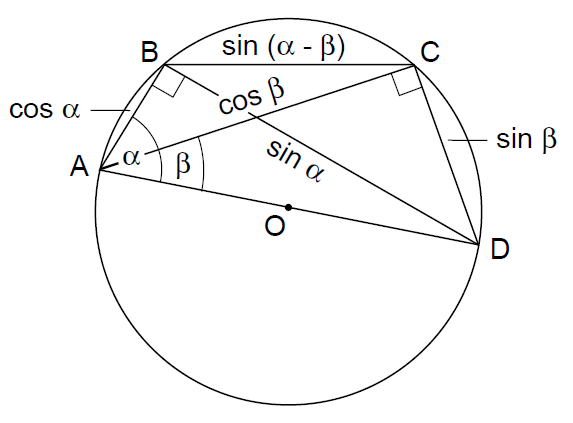
------------------图38 sin(α-β) = sinα.cosβ - cosα.sinβ的几何证明----------

因此，Ptolemy已经知道三角学中可能是最重要的一个公式，他在计算他的和弦表时使用它发挥了巨大作用；Hipparchus很可能在(Ptolemy之前)两个半世纪前就已经发现了它。古老的格言仍然是正确的：“太阳底下没有新鲜事。”

注释和文献来源：

1. Euclid的<<The Elements>>(几何原理)由Thomas Heath先生翻译(成英文),并作导读和评注(Annapolis: St. John’s College Press, 1947版),卷2，第46-49页。

2. Tobias Dantzig，在他的书<<The Bequest of the Greeks>>(希腊人的遗赠) (New York: Charles Scribner’s Sons, 1955版),第173页中指出，这个定理可能已经被Apollonius发现了，他生活在Ptolemy出生前的三个世纪。

3. Euclid的<<The Elements>>(几何原理) 卷2，第225-228页。

4. Loomis, <<The Pythagorean Propositon>>(1940初版; Washington, D.C.:全国数学教师委员会, 1968重印)，第66页。256个证明中没有一个依赖于三角学：“[毕达哥拉斯定理] 没有三角学证明，因为三角学的所有基本公式本身都是基于勾股定理的真实性……, 三角学“是”,因为勾股定理“是”(第244 页)。在这些证明中，有一个(编号231)由James A. Garfield于1876 年提出(propose)，那是在他成为美国总统之前的五年。