清华计算几何-ConvexHull(凸包)-求极点InTriangle/ToLeft Test

news2024/9/16 19:12:50

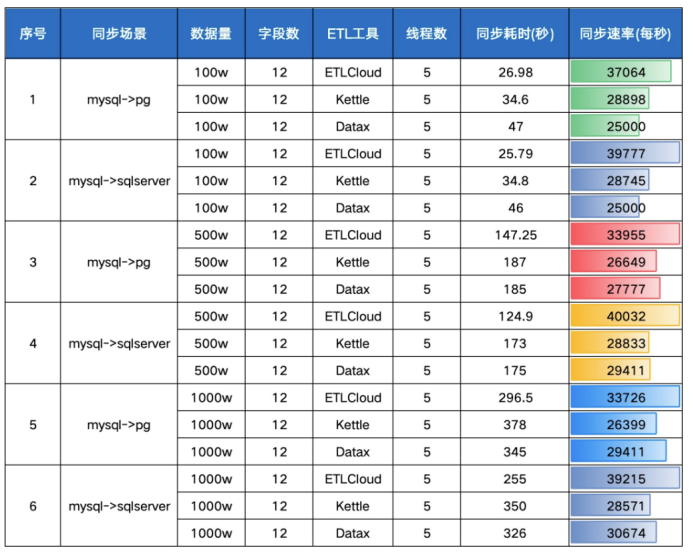
ConvexHull(凸包)

凸包是什么

凸包是计算几何一个非常基础核心的概念。我理解的凸包就是给定一个点集合, 最外围的点的包围体就是凸包。如下所示:

极点(ExtremityPoint)

给定的点集合中, 如果一个点存在一条直线, 让其他所有点都在于该直线的同一侧, 则该点为极点。

非极点

和极点性质相反, 经过该点任一直线都无法做到让其他所有点位于同一侧

凸集合

给定一个点集合S = [P1, P2...Pn], 给每个点分配一个权重rx, 满足条件:

[1]rx >= 0 &&rx <= 1,

[2]r1 + r2 + ...... rn = 1.0

由 P = r1 * P1 + ..... + Pn * rn 计算公式, 得到新的点集合，成为S的凸组合.

我理解的是点S构成的凸包内部的点集合就是凸组合。

凸相关

给定一个点集合S, 加入一个点A后，凸组合没变化的，就称点A和点集合S是凸相关的。

换一个说法就是, 点A包含在集合S里的凸组合里。

比如给定点S = {1, 4}, 点2或者点3和集合S是凸相关。

凸无关

给定一个点集合S, 加入一个点A后，凸组合发生变化, 就称点A和点集合S是凸无关。

对于点集合S(1, 2, 3), 点4是凸无关.

给定点集合求极点

分解问题

极点满足：不在点集合构成的所有三角形内部的点, 则为极点。反之为非极点。

伪代码实现

算法复杂度为O(n4)

算法实现

In-Trianle-Test

In-Trianle-Test: 判断一个点是否在一个三角形内.

如果点S在三角形三条边的同一侧, 则在三角形内. 分解为三次ToLeft测试，即点和三角形的三条边的测试.

ToLeft测试

ToLeft测试就是用于判断点是否在一条边的左侧.

叉积面积正负来判断左侧 or 右侧

(CCW 的时候ToLeft 世界左侧返回True, CW的时候ToLeft 世界左侧返回False)

代码实现

给定点集合

代码实现

#include <iostream>
#include <vector>

using namespace std;

struct Point
{
	float x;
	float y;
};


float Area2(const Point& inPointA, const Point& inPointB, const Point& inPointC)
{
	float value =
		inPointA.x * inPointB.y - inPointA.y * inPointB.x
		+ inPointB.x * inPointC.y - inPointB.y * inPointC.x
		+ inPointC.x * inPointA.y - inPointC.y * inPointA.x;

	return value;
}


bool IsLeftTest(const Point& inPointA, const Point& inPointB, const Point& inPointC)
{
	return Area2(inPointA, inPointB, inPointC) > 0;
}


bool IsInTrianle(const Point& inPoint, const Point& triangleA, const Point& triangleB, const Point& triangleC)
{
	bool bLeftA = IsLeftTest(triangleA, triangleB, inPoint);
	bool bLeftB = IsLeftTest(triangleB, triangleC, inPoint);
	bool bLeftC = IsLeftTest(triangleC, triangleA, inPoint);

	return (bLeftA == bLeftB) && (bLeftB == bLeftC);
}


void GetConvexPointSet(const vector<Point>& inPoints, vector<Point>& outPoints)
{
	int pointNum = inPoints.size();
	vector<bool> extrmeFlags;
	extrmeFlags.resize(pointNum);
	for (int index = 0; index < pointNum; index++)
	{
		extrmeFlags[index] = true;
	}

	// O(n4)
	for (int idxA = 0; idxA < pointNum; idxA++)
	{
		for (int idxB = idxA + 1; idxB < pointNum; idxB++)
		{
			for (int idxC = idxB + 1; idxC < pointNum; idxC++)
			{
				for (int s = 0; s < pointNum; s++)
				{
					if (s == idxA || s == idxB || s == idxC || !extrmeFlags[s])
						continue;


					if (IsInTrianle(inPoints[s], inPoints[idxA], inPoints[idxB], inPoints[idxC]))
					{
						extrmeFlags[s] = false;
					}
				}
			}
		}
	}

	for (int index = 0; index < pointNum; index++)
	{
		if (extrmeFlags[index])
		{
			outPoints.push_back(inPoints[index]);
		}
	}

}


int main()
{
    std::cout << "Hello World!\n";

	// point set contruct
	vector<Point> inPoints =
	{
		{0, 0},
		{-1, -1},
		{5, 2},
		{4, 5},
		{3, 3},
		{-1, 3},
		{2, 2},
		{-3, 2},
	};

	vector<Point> outPoints;
	GetConvexPointSet(inPoints, outPoints);
	for (int index = 0; index < outPoints.size(); index++)
	{
		printf("(%f, %f)\n", outPoints[index].x, outPoints[index].y);
	}

}

运行结果

很显然漏掉了 (-1, -1, -1, -1)

原因是(-1, -1), (0, 0) (2, 2), (3, 3)四点共线导致ToLeft测试失效，误认为也在三角形内部。所以得改进检测算法。

改进In-Trianle-Test

在进行In-Trianle-Test的时候先判断是否四点共线，然后在进行ToLeftTest

bool IsInTrianle(const Point& inPoint, const Point& triangleA, const Point& triangleB, const Point& triangleC)
{
	float a_area2 = Area2(triangleA, triangleB, inPoint);
	float b_area2 = Area2(triangleB, triangleC, inPoint);
	float c_area2 = Area2(triangleC, triangleA, inPoint);

	if (a_area2 == 0 && b_area2 == 0 && c_area2 == 0)
		return false;

	bool bLeftA = a_area2 > 0;
	bool bLeftB = b_area2 > 0;
	bool bLeftC = c_area2 > 0;

	// 取决于CCW/CW
	return (bLeftA == bLeftB) && (bLeftB == bLeftC);
}