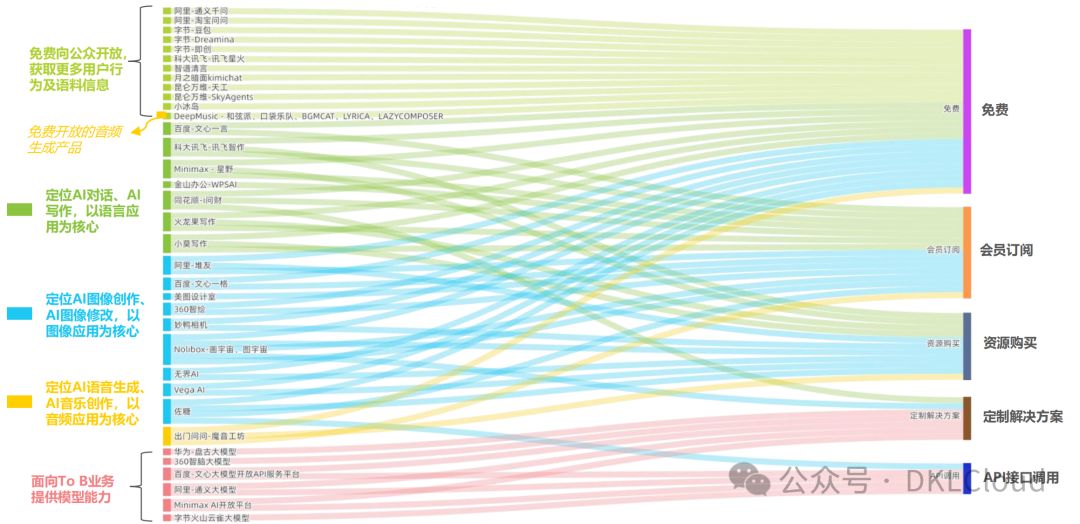
42. 接雨水

参考
思路1: 暴力解法
- 找每个柱子的左右高度
- 超时 O(N^2)

思路2: 双指针优化

class Solution {
public:
int trap(vector<int>& height) {
vector<int> lheight(height.size(), 0);
vector<int> rheight(height.size(), 0);
lheight[0] = height[0];
for (int i = 1; i < height.size(); i++) {
lheight[i] = max(lheight[i - 1], height[i]);
}
rheight[height.size() - 1] = height[height.size() - 1];
for (int i = height.size() - 2; i >= 0; i--) {
rheight[i] = max(rheight[i + 1], height[i]);
}
int res = 0;
for (int i = 0; i < height.size(); i++) {
if (i == 0 || i == height.size() - 1) continue;
int min_val = min(lheight[i], rheight[i]);
if (min_val - height[i] > 0) res += min_val - height[i];
}
return res;
}
};
思路3: 单调栈

class Solution {
public:
int trap(vector<int>& height) {
int res = 0;
stack<int> mystack;
mystack.push(0);
for (int i = 1; i < height.size(); i++) {
if (height[i] < height[mystack.top()]) {
mystack.push(i);
} else if (height[i] == height[mystack.top()]) {
mystack.push(i);
} else {
while (!mystack.empty() && height[i] >= height[mystack.top()]) {
int right = i;
int mid = mystack.top();
mystack.pop();
if (mystack.empty()) break;//元素数量不满足时, 无需回退上一步的pop操作, 放心舍弃元素(构不成封闭区间)
int left = mystack.top();
int w = right - left - 1;
res += (min(height[left], height[right]) - height[mid]) * w;
}
mystack.push(i);
}
}
return res;
}
};
//对比: 细节处理存在问题, 虽然能通过, 实际上并不是单调栈(首元素的影响)
while (mystack.size() > 1 && height[i] >= height[mystack.top()]) {
int right = i;
int mid = mystack.top();
mystack.pop();
int left = mystack.top();
int w = right - left - 1;
if (min(height[left], height[right]) - height[mid] > 0)
res += (min(height[left], height[right]) - height[mid]) * w;
}

84.柱状图中最大的矩形

思路: 单调栈
和接雨水相似, 区别在栈内元素轻的沉底
首插入0避免出现栈内元素不满足2的情况(如 3 1 2)
尾插入0避免出现一直满足栈条件而无法收获结果的情况(如 2 3 4 5)

class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
heights.insert(heights.begin(), 0);
heights.push_back(0);
stack<int> mystask;
mystask.push(0);
int res = 0;
for (int i = 1; i < heights.size(); i++) {
if (heights[i] > heights[mystask.top()]) {
mystask.push(i);
} else if (heights[i] == heights[mystask.top()]) {
mystask.push(i);
} else {
while (!mystask.empty() &&
heights[i] < heights[mystask.top()]) {
int right = i;
int mid = mystask.top();
mystask.pop();
if (!mystask.empty()) {
int left = mystask.top();
int tem = (right - left - 1) * heights[mid];
res = max(res, tem);
}
}
mystask.push(i);
}
}
return res;
}
};
思路: 双指针
实现方式不同, 此处存放的是下标索引

class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int res = 0;
vector<int> L_index(heights.size());
vector<int> R_index(heights.size());
for (int i = 0; i < heights.size(); i++) {
int t = i;
while (t > 0 && heights[t - 1] >= heights[i])
t = L_index[t - 1];//若改为 t--则会超时
L_index[i] = t;
}
for (int i = heights.size() - 1; i >= 0; i--) {
int t = i;
while (t + 1 < heights.size() && heights[i] <= heights[t + 1])
t = R_index[t + 1];
R_index[i] = t;
}
for (int i = 0; i < heights.size(); i++) {
int W = R_index[i] - L_index[i] + 1;
int tem = W * heights[i];
res = max(res, tem);
}
return res;
}
};