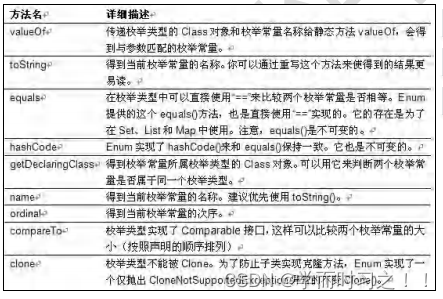
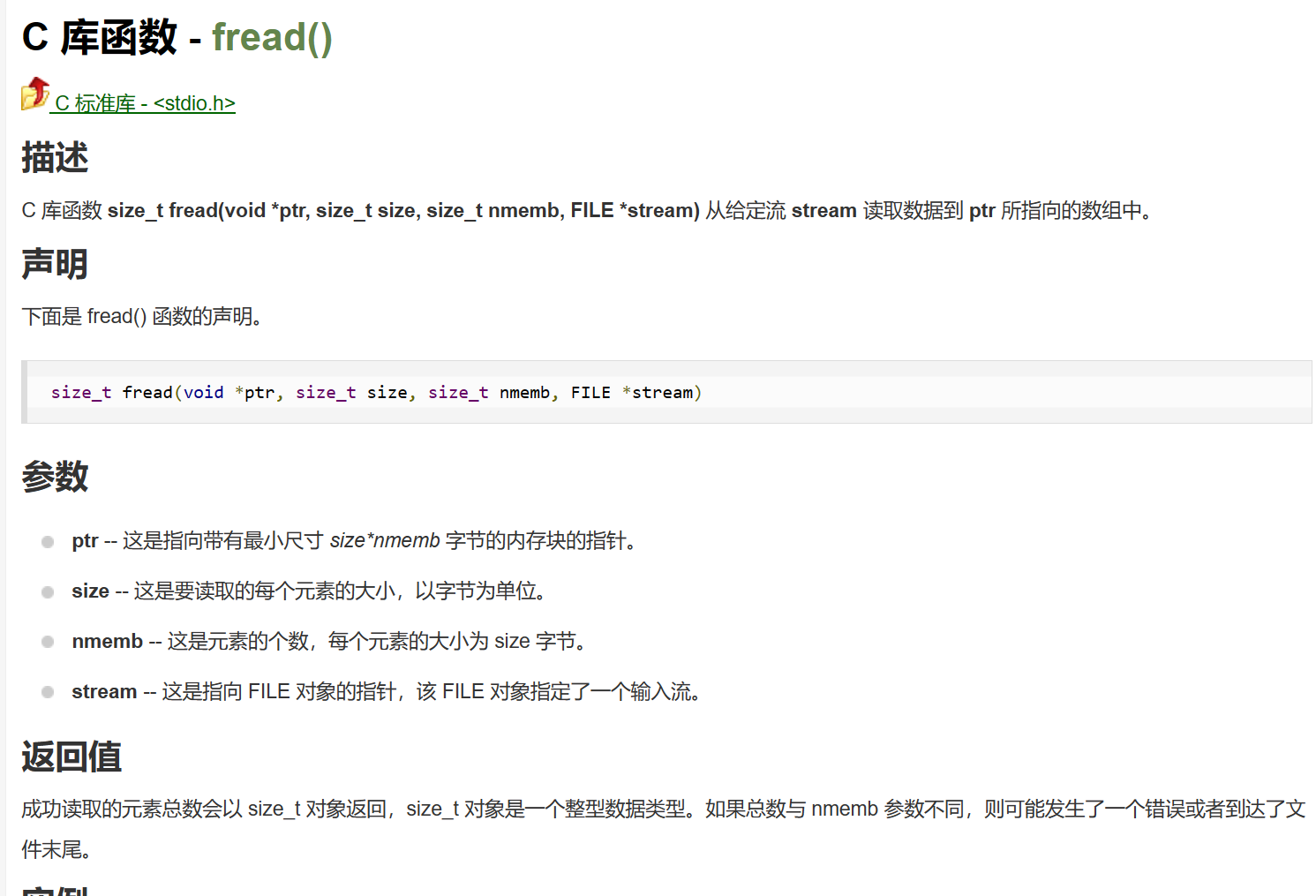
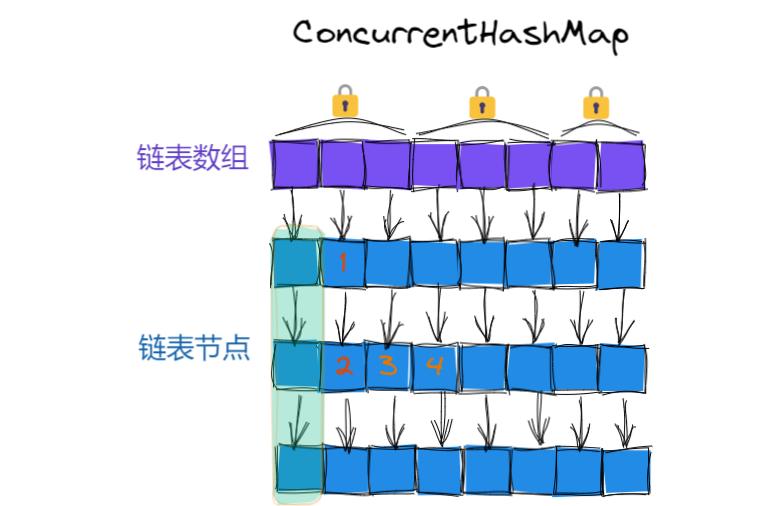
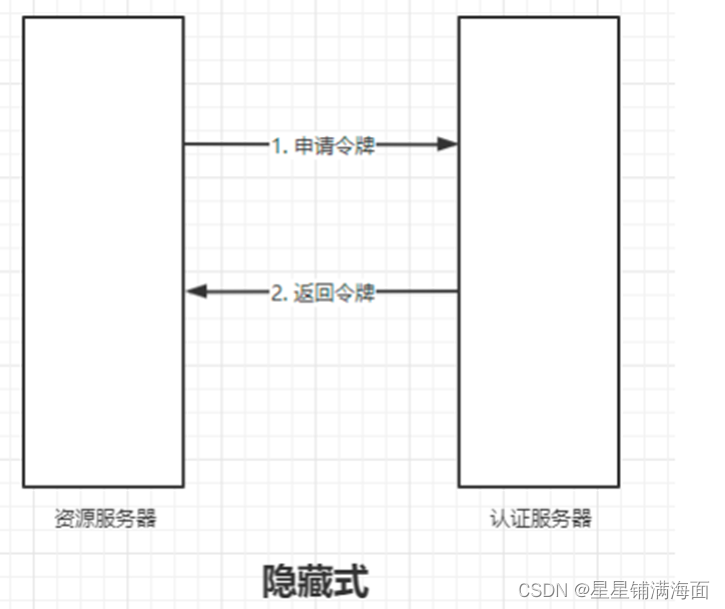
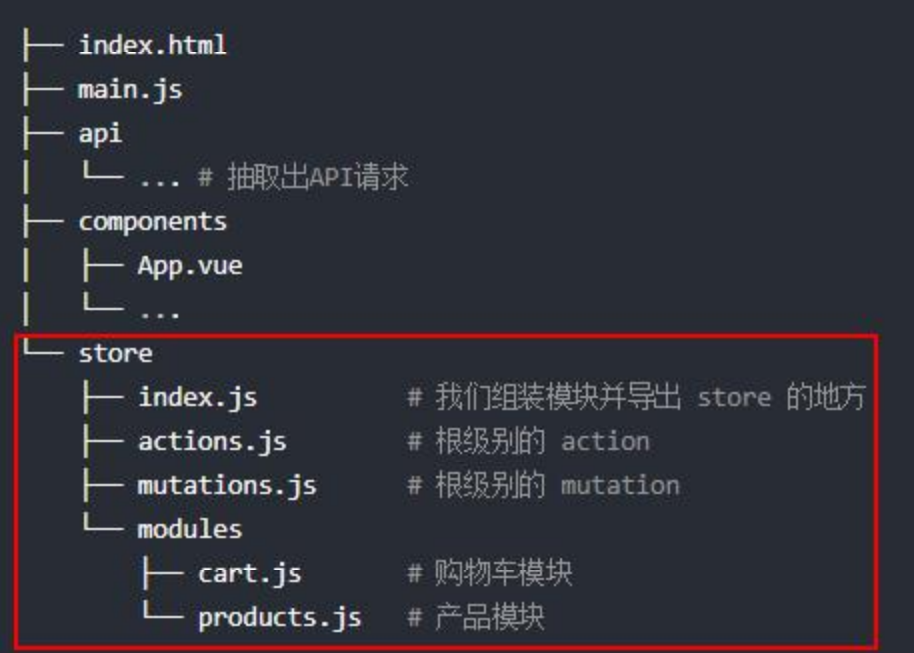
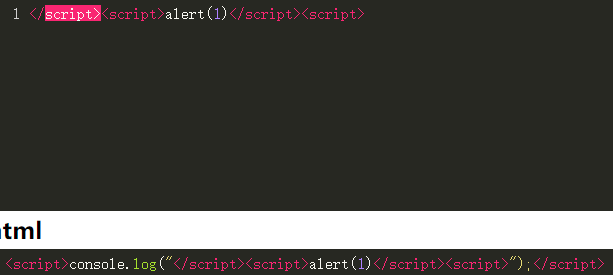
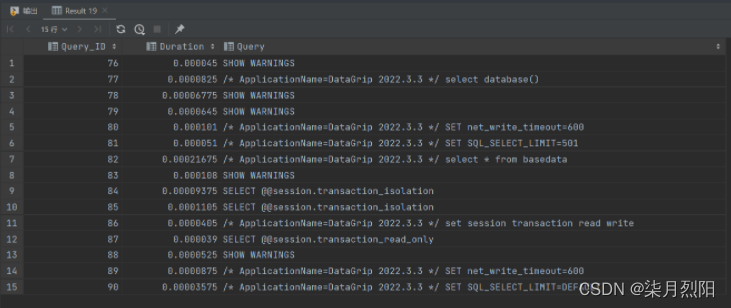
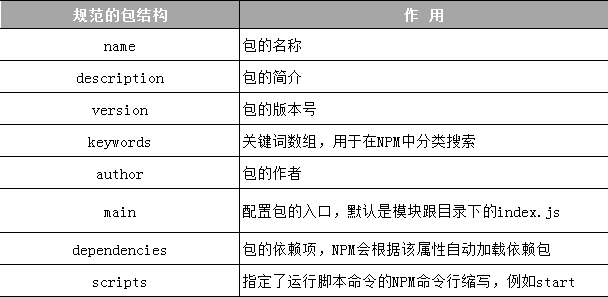
先看知识结构图

一 置信区间 定义
定义: 设
σ
\sigma
σ 为总体的未知参数,
θ
^
1
=
θ
^
1
(
x
1
,
x
2
,
.
.
.
,
x
n
)
,
θ
^
2
=
θ
^
2
(
x
1
,
x
2
,
.
.
.
,
x
n
)
\hat \theta_1 =\hat\theta_1(x_1,x_2, ..., x_n), \hat \theta_2 =\hat\theta_2(x_1,x_2, ..., x_n)
θ^1=θ^1(x1,x2,...,xn),θ^2=θ^2(x1,x2,...,xn)是由样本
x
1
,
x
2
,
.
.
.
,
x
n
x_1, x_2, ..., x_n
x1,x2,...,xn定出的两个统计量, 若对于给定的概率 1 —
α
\alpha
α ( 0<
α
\alpha
α < 1), 有
则随机区间[
θ
^
1
\hat\theta_1
θ^1 ,
θ
^
2
\hat\theta_2
θ^2]称为参数
θ
\theta
θ 的置信度为
1
−
α
1-\alpha
1−α 的置信区间,
θ
^
1
\hat\theta_1
θ^1 称为置信下限,
θ
^
2
\hat\theta_2
θ^2 称为置信上限。