目录
思考建模思路
例1
定义date
创建时间序列模拟器
结果分析
例2
序列图
创建时间序列模型
未除去异常值
剔除有异常值
勾选
结果
注
思考建模思路
( 1 )处理数据的缺失值问题、生成时间变量并画出时间序列图;( 2 )数据是否为季度数据或者月份数据(至少有两个完整的周期,即两年),如果是的话则要观察图形中是否存在季节性波动(加法和乘法)( 3 )根据时间序列图大致判断数据是否为平稳序列(数据围绕着均值上下波动,无趋势和季节性)( 4 ) Spss创建传统模型,看看 Spss专家建模器得出的最优的模型类型。( 5 )如果最后的结果是 ARIMA(p,0,q) 模型(也就是ARMA),那么我们就可以画出时间序列的样本 ACF和 PACF 图形进行分析;如果得到的是 ARIMA(p,1,q) 模型,我们可以先对数据进行 1阶差分后再用 ACF 和PACF 图形分析;如果得到的结果与季节性相关,那么我们可以考虑使用时间序列分解。
(1) 一般比较两个模型的好坏,我们可以使用平稳的 R 方(文档上翻译成了固定的 R 方)或者标准化BIC ( BIC 准则),这两个指标既考虑了拟合的好坏,又考虑了模型的复杂度;(2)R 方可用来反映线性模型拟合的好坏,越接近于 1 拟合的越准确。
例1
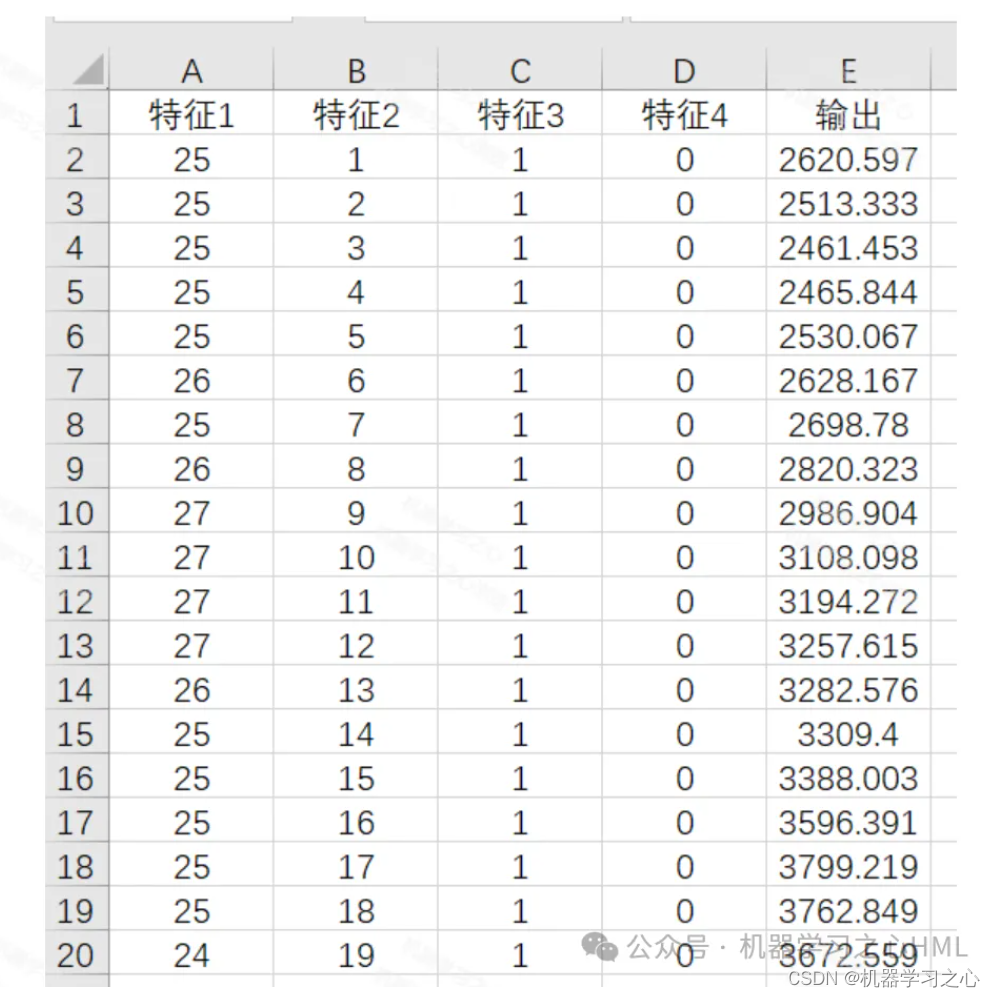
根据某产品2014-2018年季度销售数据,预测未来两年的销售数据。
定义date

创建时间序列模拟器
按照下面示例图进行勾选就行



勾选ACF和PACF图,我们需要观察他们是否拖尾或截尾


结果分析
spss专家建模为我们选择了温特斯加性模型

R2越接近1拟合效果越好

spss中直接帮你选择BIC最小

p值大于0.05, 没有白噪声

结论:从残差的 ACF 和 PACF 图形中可以看出,所有滞后阶数的自相关系数和偏自相关系数均和0 没有显著的差异;另外从表可以看出,对残差进行Q 检验得到的 p 值为0.741 ,即我们无法拒绝原假设,认为残差就是白噪声序列,因此温特加法模型能够很好的识别本例中的销量数据。
写论文时需要写进去


例2
给定 2016/01/04 至 2019/08/07 的上证指数,请对其进行建模,并预测接下来一段时间的指数走势。
定义date
本题定义date与上一题有所不同,本题的时间不是连续的,股票会有收市的时间,所以定义时直接使用“天”

序列图

创建时间序列模型
未除去异常值

spss为我们选择了simple模型

p值为0 ,残差不是白噪声,模型效果并不好,从下面的图也可以看出来,ACF与PACF都出现了拖尾,并不满足此模型的特点。



从预测值也可以看出不对劲,预测出来的数据都一样 ,这个我们之前也讲过,simple模型只能预测下一个数值。
因为这个是股票数据,使用我们考虑是未除去异常值,下面展示除去异常值做法
剔除有异常值
勾选
条件-离群值

结果






从上面这些评估指标来看模型的效果好像还不错,但是实际中预测并没有这么简单
然后我们还发现,在第14个预测值后,后面的值都是一样的,这也是模型的弊端


注意:我们将波动较大的数据看成了异常值,事实上有更加复杂的模型可以捕捉到这些异常值,例如GARCH模型(广义的自回归条件异方差模型)
时间序列分析之GARCH模型介绍与应用-CSDN博客(这篇文章可以,里面有py代码)
注
预测两要:一要结合背景;(例如某些政策的影响,例如GDP增速)二要合理假设。预测两不要 :不要硬套模型;不要不做解释