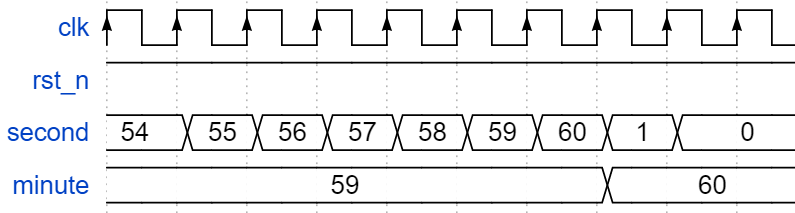
OK,看我们题目就可知道啦,今天要分享学习的一种数据结构就是二叉搜索树。
内容题目也说了三个大概的,分别是寻找、插入、删除。
讲这个之前呢,那么就先讲讲这个二叉搜索树是何方神圣呢?
二叉搜索树:
又称二叉排序树,它或者是一颗空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上的所有节点的值都小于根节点的值。
若它的右子树不为空,则右子树上的所有节点的值都大于根节点的值。
它的左右子树也分别为二叉搜索树
示例如下:

OK,讲完了这个概念,那么接下来这个操作内容吧。
首先创建这个节点先
public class SearchTree {
class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val){
this.val=val;
}
}
public TreeNode root=null;
}以及把这个节点初始一个变量root,置为null。
接下来,就写这个简单的方法——查找
查找
public TreeNode search(int key){
TreeNode cur=root;
while(cur!=null){
if(cur.val<key){
cur = cur.right;
}
else if(cur.val>key){
cur=cur.left;
}else{
return cur;
}
}
return null;
}思路:
让一个cur的节点帮我去走,因为root的左边比root小,右边比root大,所以当cur.val小于key时,说明key大往右走,否则往左走,都不是,即找到了,就可以返回当前节点的值了。
插入
先上代码
public void insert(int val){
TreeNode node=new TreeNode(val);
if(root==null){
root=node;
return;
}
TreeNode cur=root;
TreeNode parent=null;
while(cur!=null){
if(cur.val>val){
parent=cur;
cur=cur.left;
}else if(cur.val<val){
parent=cur;
cur=cur.right;
}else{
return;
}
}
if(parent.val>val){
parent.left=node;
}else{
parent.right=node;
}
}思路:
先定义好一个Node节点,保存要插入的信息,然后再定义一个parent节点来保存上一个节点的信息,为什么呢?
因为这个总体思路就是要插入的节点的值比这个当前root节点的值进行比大小,大于root就往右走,小于往左走。
接着,再定义一个cur的节点,让它去走,当cur往左还是往右走时,parent都要走到当前cur的位置
当然,插入一个已有的值,可以选择return了,
当while循环走完,意味着走到了对的位置了
举个例子

插入一个2,那么这个cur就得往左走,走到1位置才是正确的,
然后parent也是到了cur的位置。
然后,当前的parent的值和当前val的值相比,大于就插入右边,小于就插入左边,
显然这个例子中,2插入1的右边。
最后一个内容。
删除
这里的删除有些麻烦,要分三种情况
第一种情况
删除的节点左边为空
举个例子

这个当左边为空时,也有三种状况。
第一种:当root为删除的节点时,让root=cur.right
第二种:当cur为根节点的左边时,图中为3,既让root=cur.right
第三种:当cur为根节点的右边时,图中为7,既让root=cur.right
而根据这里我们也可以写出第一部分的代码了
public void remove(int key){
TreeNode parent=null;
TreeNode cur=root;
while(cur!=null){
if(cur.val<key){
parent=cur;
cur=cur.right;
}else if(cur.val>key){
parent=cur;
cur=cur.left;
}else{
removeNode(parent,cur);
}
}
}
private void removeNode(TreeNode parent,TreeNode cur){
if(cur.left==null){
if(cur==root){
root=cur.right;
}else if(cur==parent.left){
parent.left=cur.right;
}else {
parent.right=cur.right;
}
}代码解释:同样的,我们删掉节点之前,也先需要找到这个节点,删除节点的事让removeNode来做。
刚刚说明的root=cur.right中的root,当然是让一个parent来记录下来(即cur前面节点的信息)
第二种情况
即删除的节点右边为空
举个例子

同样的,这里也有三种情况
第一种:当删除的节点为根节点,所以root=cur.left
第二种:当删除的节点为root的左边,图中为3,所以root=cur.left
第三种:当删除的节点为root的右边,图中为7,所以root=cur.left
所以到这里也可以写一些代码了
private void removeNode(TreeNode parent,TreeNode cur){
if(cur.left==null){
if(cur==root){
root=cur.right;
}else if(cur==parent.left){
parent.left=cur.right;
}else {
parent.right=cur.right;
}
}else if(cur.right==null){
if(cur==root){
root=cur.left;
}else if(cur==parent.left){
parent.left=cur.left;
}else{
parent.right=cur.left;
}这个代码,跟第一种情况是类似的。
第三种情况
即删除的节点左右都不为空
目录
二叉搜索树:
查找
插入
删除
第一种情况
第二种情况
第三种情况
完!
举个例子

当我们要删除的节点为cur时,即图中的60,我们采用的方法是替换法,
即其一的办法是,在cur的右边找到其最小值替换掉cur,即图中的65替换掉60。
同理也可以找到cur的左边的最大值替换掉cur,
这样做是因为可以保持整棵树为一个二叉搜索树
具体这样子做(以在cur的右子树找最小值为例)
定义两个节点,一个是target,一个是targetParent。
其中,target=cur.right
targetParent=cur
让这个target去找到其最小值,找到了,再去赋值然后更新要修改的节点
修改完成后,再像其第一种情况中的当targetParent的左边为空时,让这个targetParent的左边指向
target的右边,相当于指向一个空指针,使其不再引用这个65的节点,达到删除效果
上代码
TreeNode target=cur.right;
TreeNode targetParent=cur;
while(target !=null){
targetParent=target;
target =target.left;
}
cur.val=target.val;
if(target ==targetParent.left){
targetParent.left=target .right;
}else{
targetParent.right=target .right;
}
}