目录

1、红黑树的概念

2、红黑树的性质

 3、红黑树节点的定义

4、红黑树的插入

5、红黑树验证

代码汇总

6、红黑树的删除（了解）

7、红黑树的应用

8、红黑树 VS AVL树

---

1、红黑树的概念

        红黑树，就是一种特殊的二叉搜索树，每个节点会增加一个存储位来表示颜色，可以是红色或者黑色（Red/Black）

        通过对于任何一条从根节点到叶子节点的路径上各个节点着色方式的限制，红黑树确保没有一条路径会比其路径长出两倍，因此是红黑树是接近平衡的

---

2、红黑树的性质

• 最长路径最多是最短路径的2倍
• 每个节点不是红色就是黑色
• 根节点是黑色的
• 如果一个节点是红色的，则它的两个孩子节点是黑色的【没有2个连续的红色节点】
• 对于每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点
• 每个叶子结点都是黑色的【这里的叶子节点指的是空节点】

例如一个红黑树：

 

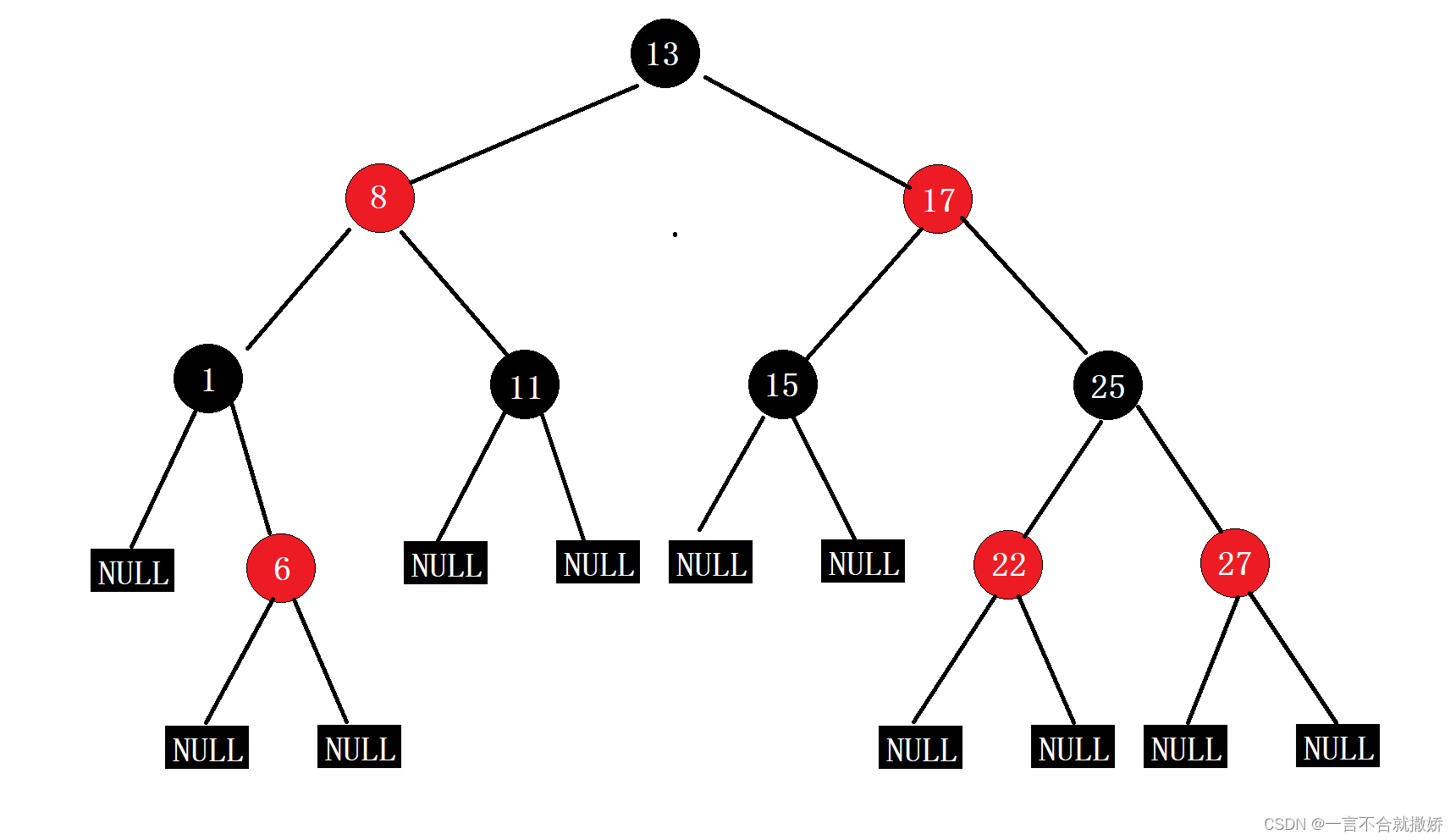
最长路径最多是最短路径的2倍：

---

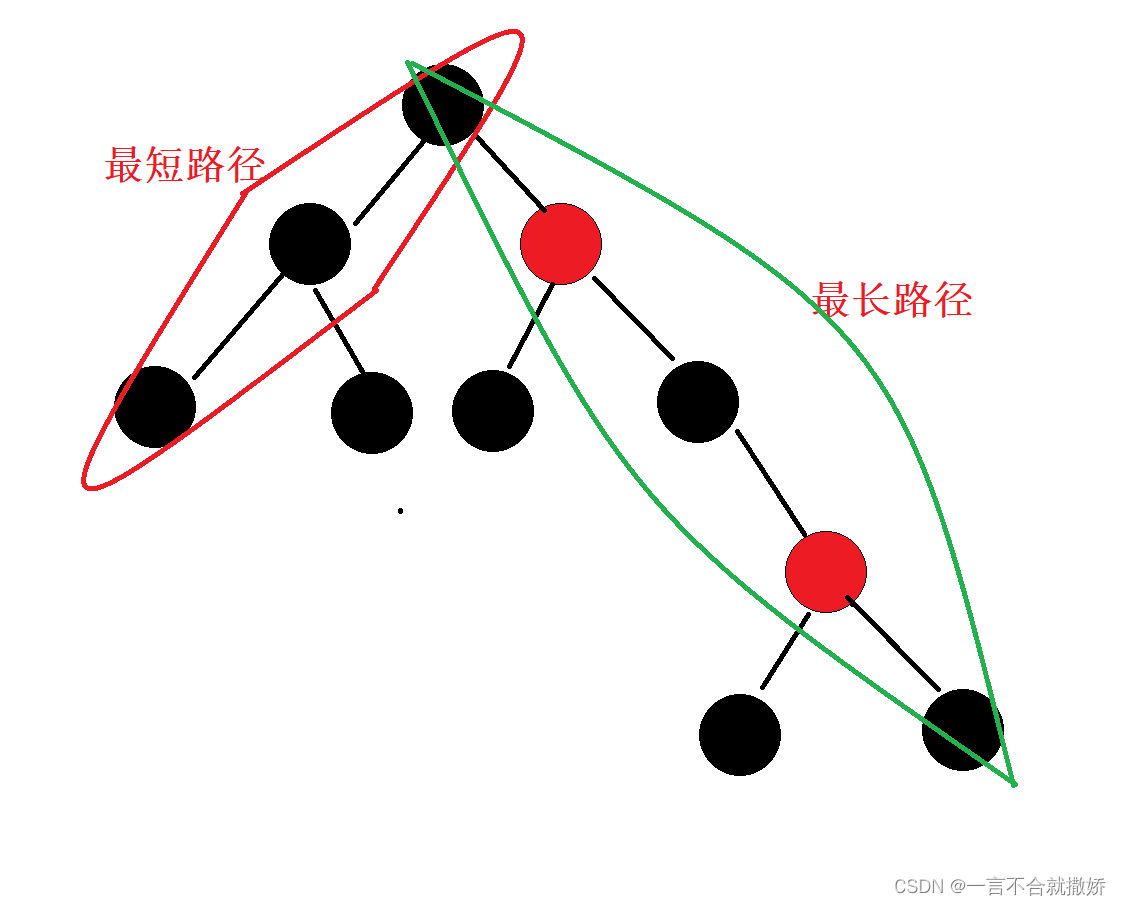
 3、红黑树节点的定义

public class RBTree {
    static class RBTreeNode {
        public RBTreeNode left;
        public RBTreeNode right;
        public RBTreeNode parent;
        public int val;
        public COLOR color;

        public RBTreeNode(int val) {
            this.val = val;
            //默认新创建的节点为红色
            this.color = COLOR.RED;
        }
    }
    
    public RBTreeNode root;
    

}

其中COLOR是一个枚举类型：

public enum COLOR {
    RED,BLACK
}

---

4、红黑树的插入

        同AVL树类似理解，他们都是在二叉搜索树上加上平衡限制条件，so？红黑树的插入也是分为两步：

• 按照二叉搜索树的规则插入新节点
• 检测新节点插入后，如果红黑树的性质遭到破坏，则对其进行修改

二叉搜索树的插入：

    /**
     * 插入节点
     * @param val
     * @return
     */
    public boolean insert(int val) {
        RBTreeNode node = new RBTreeNode(val);
        RBTreeNode cur = root;
        RBTreeNode parent = null;
        while (cur != null) {
            if(cur.val > val) {
                parent = cur;
                cur = cur.left;
            } else if(cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else {
                return false;
            }
        }
        if(parent.val < val) {
            parent.right = node;
        } else {
            parent.left = node;
        }
        
        node.parent = parent;
        cur = node;
        
        //红黑树，调整颜色
        //...
    }

        因为加入的新节点其颜色默认是红色，因此：

• 如果它的双亲节点的颜色是黑色，则没有违反红黑树的任何规则，就不需要对其调整；
• 如果新加入节点的双亲节点颜色为红色时，就违反了性质【红色节点不能连在一起】，需要进行调整

约定：cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

如果不懂左右单旋的伙伴们，可以回顾一下： http://t.csdn.cn/3PyVW

• 情况一：cur为红，p为红，g为黑，u存在且为红

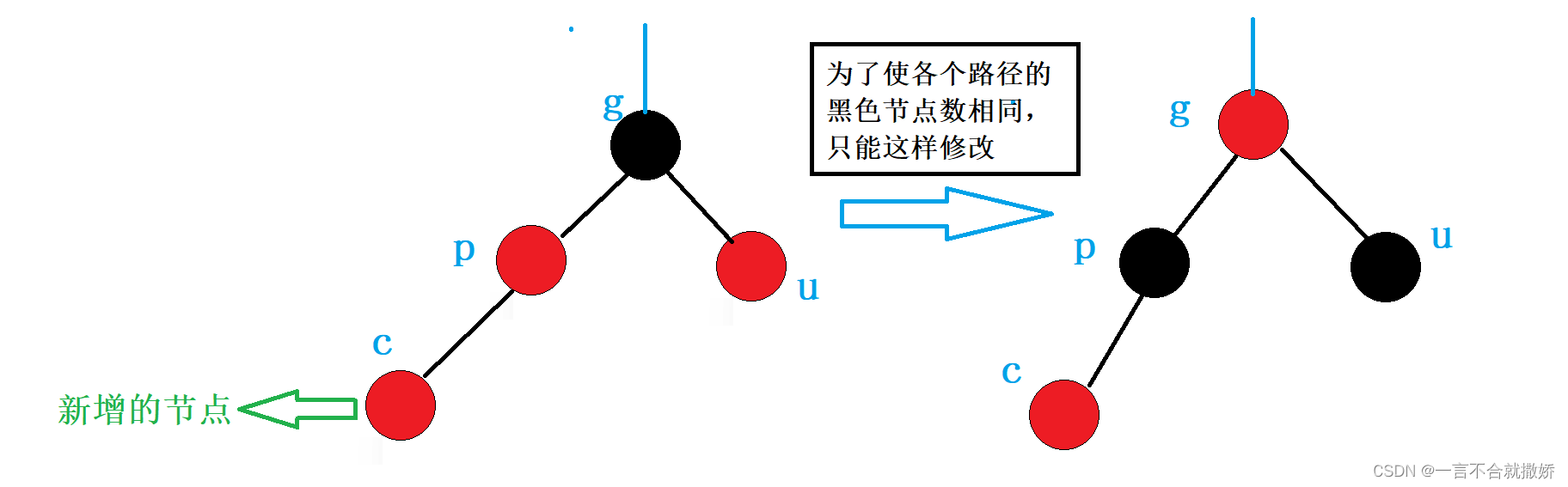
• 如果g是根节点，调整完成后，需要将g改为黑色 
• 如果g是子树，g一定有双亲，且g的双亲如果是红色，需要继续向上调整

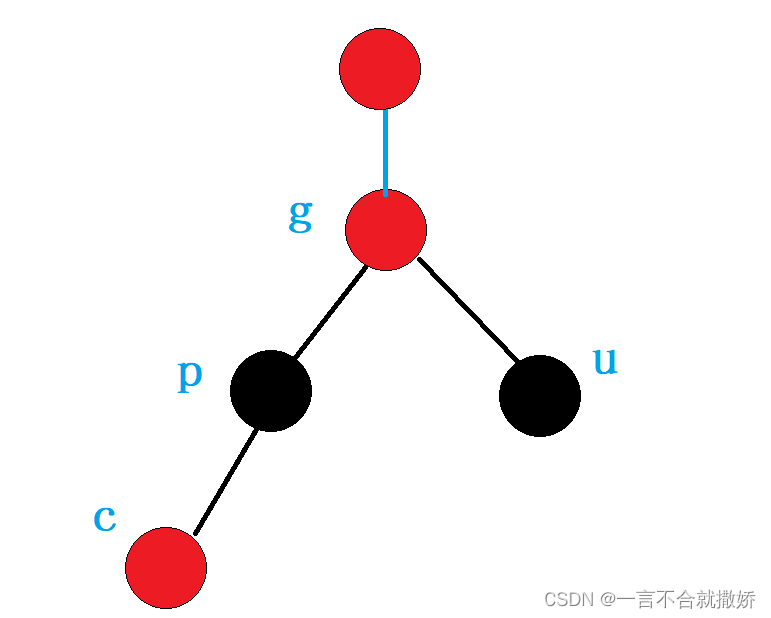
 代码：

parent.color = COLOR.BLACK;
uncle.color = COLOR.BLACK;
grandFather.color = COLOR.RED;
//继续向上修改
cur = grandFather;
parent = cur.parent;

• 情况2：cur为红，p为红，g为黑，u不存在/u为黑

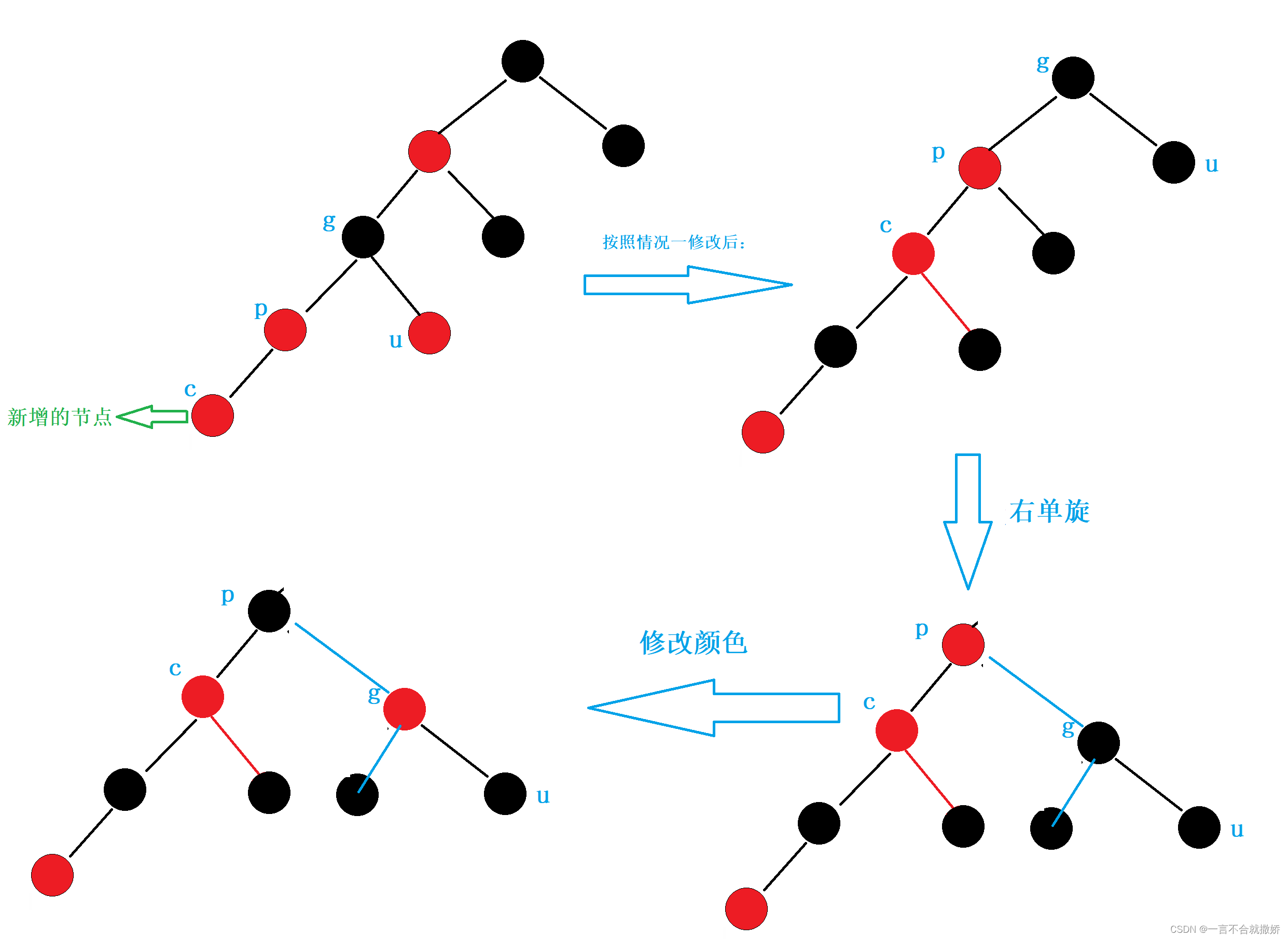
 代码：

rotateRight(grandFather);
grandFather.color = COLOR.RED;
parent.color = COLOR.BLACK;

• 情况三：cur为红，p为红，g为黑，u不存在/u为黑

代码：

                    //情况三：
                    if(cur == parent.right) {
                        rotateLeft(parent);
                        RBTreeNode tmp = parent;
                        parent = cur;
                        cur = tmp;
                    }//情况三变到了情况二
                    //情况二：
                    rotateRight(grandFather);
                    grandFather.color = COLOR.RED;
                    parent.color = COLOR.BLACK;

---

5、红黑树验证

类比于AVL树，红黑树的验证分两步：

• 检测是否满足二叉搜索树（中序遍历是否有序）
• 检测是否满足红黑树的各个性质

代码我就直接放在了代码汇总里~~~

---

代码汇总

/**
 * Created with IntelliJ IDEA.
 * Description:
 * User:龙宝
 * Date:2023-02-01
 * Time:12:45
 */
enum COLOR {
    RED,BLACK
}
public class RBTree {
    static class RBTreeNode {
        public RBTreeNode left;
        public RBTreeNode right;
        public RBTreeNode parent;
        public int val;
        public COLOR color;

        public RBTreeNode(int val) {
            this.val = val;
            //默认新创建的节点为红色
            this.color = COLOR.RED;
        }
    }

    public RBTreeNode root;


    /**
     * 插入节点
     * @param val
     * @return
     */
    public boolean insert(int val) {
        RBTreeNode node = new RBTreeNode(val);
        RBTreeNode cur = root;
        RBTreeNode parent = null;
        while (cur != null) {
            if(cur.val > val) {
                parent = cur;
                cur = cur.left;
            } else if(cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else {
                return false;
            }
        }
        if(parent.val < val) {
            parent.right = node;
        } else {
            parent.left = node;
        }

        node.parent = parent;
        cur = node;

        //红黑树，调整颜色
        //...

        while (parent != null && parent.color == COLOR.RED) {
            RBTreeNode grandFather = parent.parent;//该引用不会是空的
            if(parent == grandFather.left) {
                RBTreeNode uncle = grandFather.right;
                if(uncle != null && uncle.color == COLOR.RED) {
                    //情况一：
                    parent.color = COLOR.BLACK;
                    uncle.color = COLOR.BLACK;
                    grandFather.color = COLOR.RED;

                    //继续向上修改
                    cur = grandFather;
                    parent = cur.parent;
                } else {
                    //uncle不存在 或者 uncle是黑色的
                    //情况三：
                    if(cur == parent.right) {
                        rotateLeft(parent);
                        RBTreeNode tmp = parent;
                        parent = cur;
                        cur = tmp;
                    }//情况三变到了情况二
                    //情况二：
                    rotateRight(grandFather);
                    grandFather.color = COLOR.RED;
                    parent.color = COLOR.BLACK;
                }
            } else {
                //parent == grandFather.right
                RBTreeNode uncle = grandFather.left;
                if(uncle != null && uncle.color == COLOR.RED) {
                    parent.color = COLOR.BLACK;
                    uncle.color = COLOR.BLACK;
                    grandFather.color = COLOR.RED;
                    //继续向上修改
                    cur = grandFather;
                    parent = cur.parent;
                } else {
                    //情况三：
                    if(cur == parent.left) {
                        rotateRight(parent);
                        RBTreeNode tmp = parent;
                        parent = cur;
                        cur = tmp;
                    }//情况三变到情况二
                    //情况二：
                    rotateLeft(grandFather);
                    grandFather.color = COLOR.RED;
                    parent.color = COLOR.BLACK;
                }
            }
        }
        root.color = COLOR.BLACK;
        return true;
    }

    /**
     * 左单旋
     * @param parent
     */
    private void rotateLeft(RBTreeNode parent) {
        RBTreeNode subR = parent.right;
        RBTreeNode subRL = subR.left;

        parent.right = subRL;

        subR.left = parent;
        if(subRL != null) {
            subRL.parent = parent;
        }

        RBTreeNode pParent = parent.parent;
        parent.parent = subR;

        if(root == parent) {
            root = subR;
            root.parent = null;
        }else {
            if(pParent.left == parent) {
                pParent.left = subR;
            }else {
                pParent.right = subR;
            }
            subR.parent = pParent;
        }
    }


    /**
     * 右单旋
     * @param parent
     */
    private void rotateRight(RBTreeNode parent) {

        RBTreeNode subL = parent.left;
        RBTreeNode subLR = subL.right;

        parent.left = subLR;
        subL.right = parent;
        //没有subLR
        if(subLR != null) {
            subLR.parent = parent;
        }
        //必须先记录
        RBTreeNode pParent = parent.parent;
        parent.parent = subL;
        //检查 当前是不是就是根节点
        if(parent == root) {
            root = subL;
            root.parent = null;
        }else {
            //不是根节点，判断这棵子树是左子树还是右子树
            if(pParent.left == parent) {
                pParent.left = subL;
            }else {
                pParent.right = subL;
            }
            subL.parent = pParent;
        }
    }

    /**
     * 判断当前树 是不是红黑树
     *  得满足 红黑树的性质
     * @return
     */
    public boolean isRBTree() {
        if(root == null) {
            //如果一棵树是空树，那么这棵树就是红黑树
            return true;
        }

        if(root.color != COLOR.BLACK) {
            System.out.println("违反了性质：根节点必须是黑色的！");
        }

        //存储当前红黑树当中 最左边路径的黑色的节点个数
        int blackNum = 0;
        RBTreeNode cur = root;
        while (cur != null) {
            if(cur.color == COLOR.BLACK) {
                blackNum++;
            }
            cur = cur.left;
        }
        //检查是否存在两个连续的红色节点  && 每条路径上黑色的节点的个数是一致的
        return checkRedColor(root) && checkBlackNum(root,0,blackNum);
    }

    /**
     *
     * @param root
     * @param pathBlackNum 每次递归的时候，计算黑色节点的个数  0
     * @param blackNum 事先计算好的某条路径上的黑色节点的个数   2
     * @return
     */
    private boolean checkBlackNum(RBTreeNode root,int pathBlackNum,int blackNum) {
        if(root == null) return true;
        if(root.color == COLOR.BLACK) {
            pathBlackNum++;
        }
        if(root.left == null && root.right == null) {
            if(pathBlackNum != blackNum) {
                System.out.println("违反了性质：每条路径上黑色的节点个数是不一样的！");
                return false;
            }
        }
        return checkBlackNum(root.left,pathBlackNum,blackNum) &&
                checkBlackNum(root.right,pathBlackNum,blackNum);
    }

    /**
     * 检查是否存在两个连续的红色节点
     * @param root
     * @return
     */
    private boolean checkRedColor(RBTreeNode root) {
        if(root == null) return true;
        if(root.color == COLOR.RED) {
            RBTreeNode parent = root.parent;
            if(parent.color == COLOR.RED) {
                System.out.println("违反了性质：连续出现了两个红色的节点");
                return false;
            }
        }
        return checkRedColor(root.left) && checkRedColor(root.right);
    }

    public void inorder(RBTreeNode root) {
        if(root == null) {
            return;
        }
        inorder(root.left);
        System.out.print(root.val+" ");
        inorder(root.right);
    }

}

---

6、红黑树的删除（了解）

找替代节点【替代节点的左子树、右子树一定有一个为空】

---

7、红黑树的应用

 1. java集合框架中的：TreeMap、TreeSet底层使用的就是红黑树
2. C++ STL库 -- map/set、mutil_map/mutil_set
3. linux内核：进程调度中使用红黑树管理进程控制块，epoll在内核中实现时使用红黑树管理事件块
4. 其他一些库：比如nginx中用红黑树管理timer等

---

8、红黑树 VS AVL树

• 红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O(logN)
• 红黑树不追求绝对平衡，只保证最长路径不超过最短路径的2倍，降低了插入时旋转的次数
• 在经常进行增删的结构中，红黑树性能比AVL树更优，并且红黑树的实现相对简单，所以实际中红黑树使用更多

好啦，下期见咯~