【6s965-fall2022】量化 Quantization Ⅰ

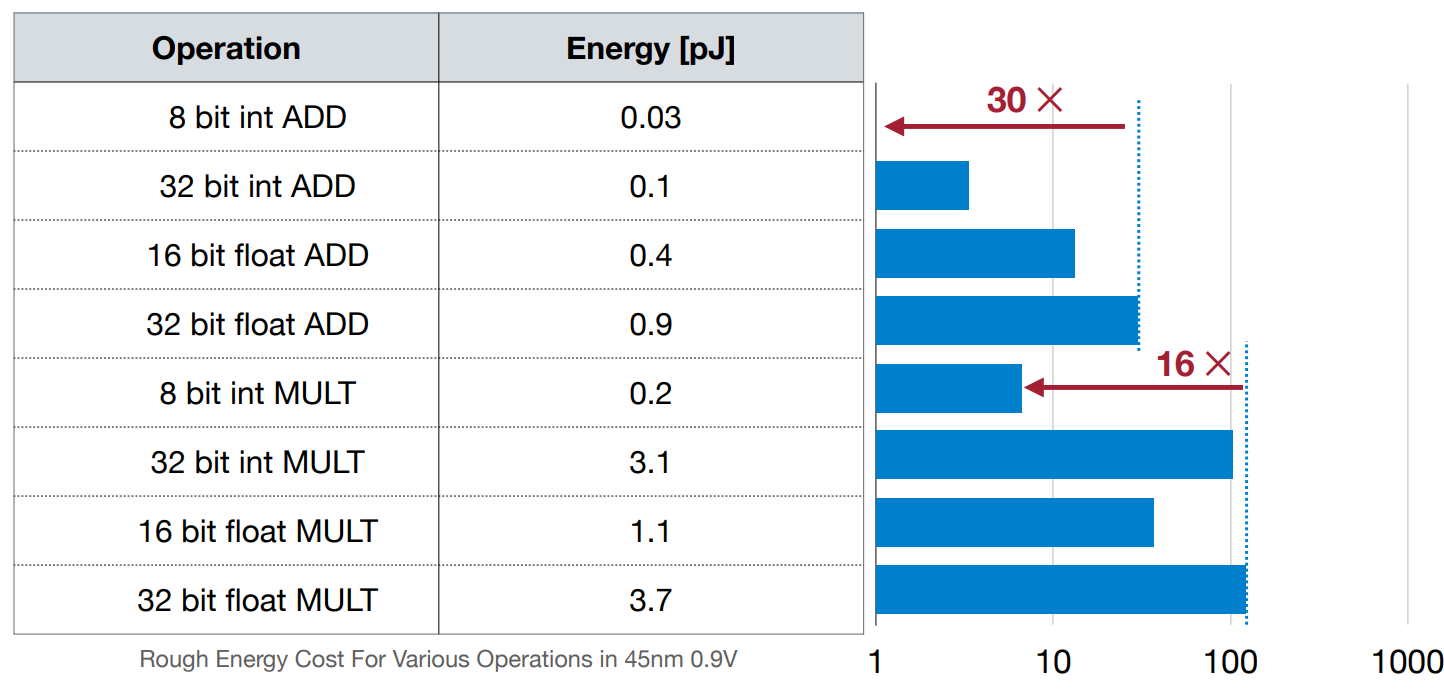
模型的大小不仅和参数量的多少有关，而且也和位宽有关。
$\#Parameter × BitWidth.$
低位宽的运算操作容易实现、运算速度快、功耗低。

在这里插入图片描述

什么是量化？

从广义上讲，量化是将连续信号变成离散信号的过程；它在信号处理（以离散的时间间隔采样）和图像压缩（减少每个像素的可能颜色空间）中很常见。

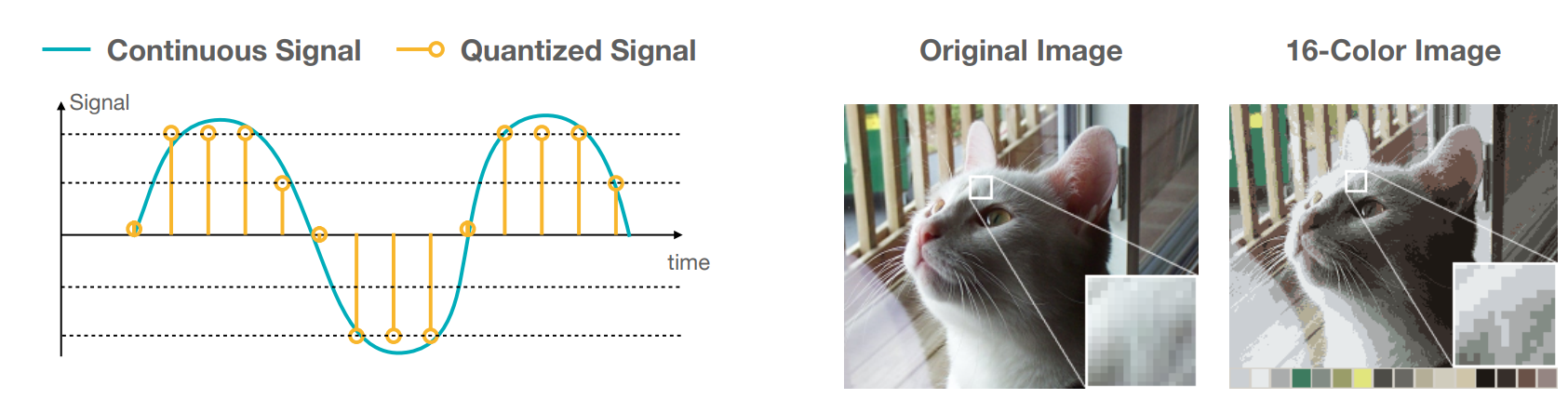
在这里插入图片描述

在这门课中，我们将量化定义为将输入从一个连续的、大范围的数值集约束为一个离散的、小范围的数值集的过程。量化的过程包括将每个权重的数据类型改为限制性更强的数据类型（即可以用更少的比特表示）。常用的量化方法有：基于K-Means的权重量化（K-Means Based Weight Quantization）和线性量化（Linear Quantization）。

在这里插入图片描述

数据类型

整数（Integers）
- 原码（Signed-Magnitude）
- 反码（Ones’ Complement）
- 补码（Two’s Complement）
定点数（Fixed Point Numbers）
浮点数（Floating Point Numbers）
- $(-1)^{\text{sign}} \times (1.\text{mantissa}) + 2^{\text{exponent} - \text{exponent bias}}$

Convention	Sign Bits	Exponent Bits	Mantissa Bits
IEEE 754	1	8	23
IEEE Half-Precision 16-bit float	1	5	10
Brain Float (BF16)	1	8	7
NVIDIA TensorFloat 32	1	8	10
AMD 24-bit Float (AMD FP24)	1	7	16

Brain Float (BF16) 是专门为神经网络而设计的数据类型，对比于IEEE Half-Precision 16-bit float ，更加看重范围，精度不如范围重要。

基于K-Means的权重量化

K-Means-based Weight Quantization [Han et al., ICLR 2016]

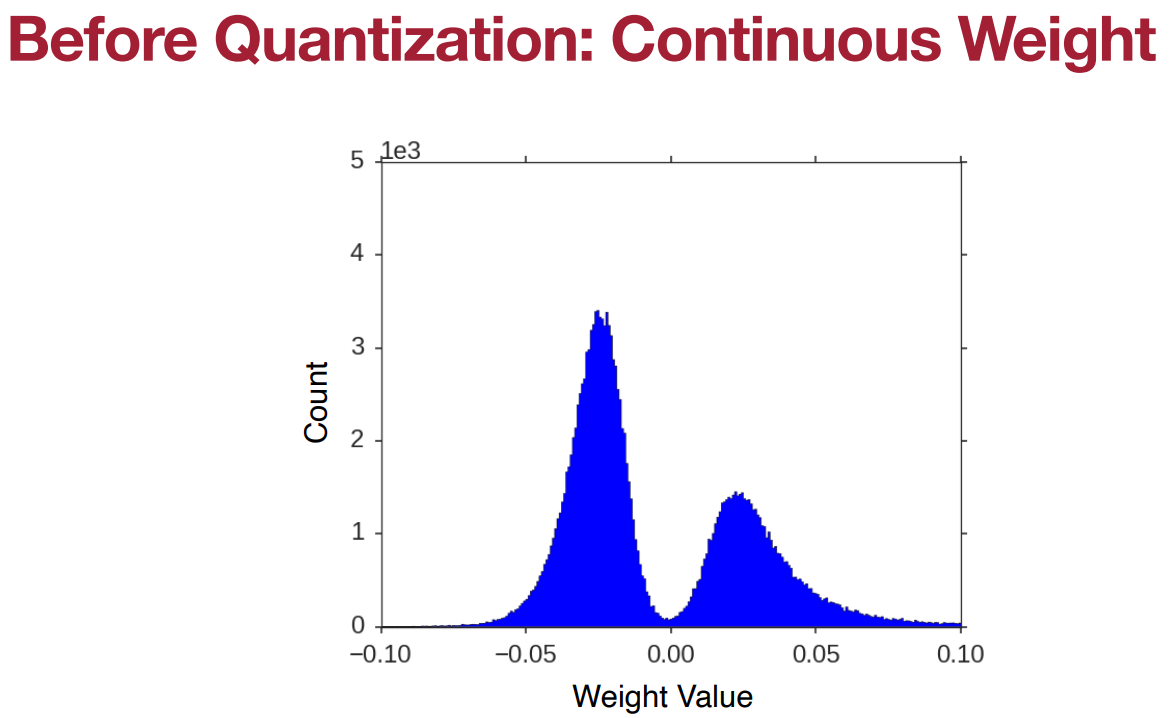
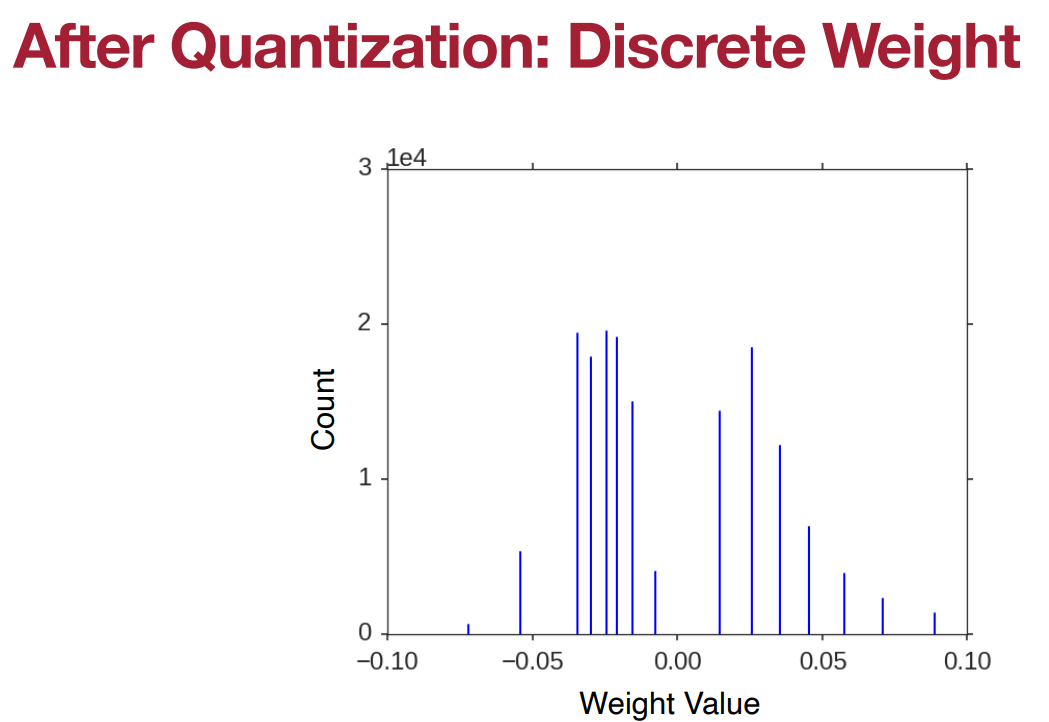
正如Brain Float (BF16) 所考虑的那样，神经网络的性能实际上并不太依赖于权重的精度。一般来说，像2.09、2.12、1.92和1.87这样的值都可以被近似为2，那么我们为什么不把权重近似成这样呢？

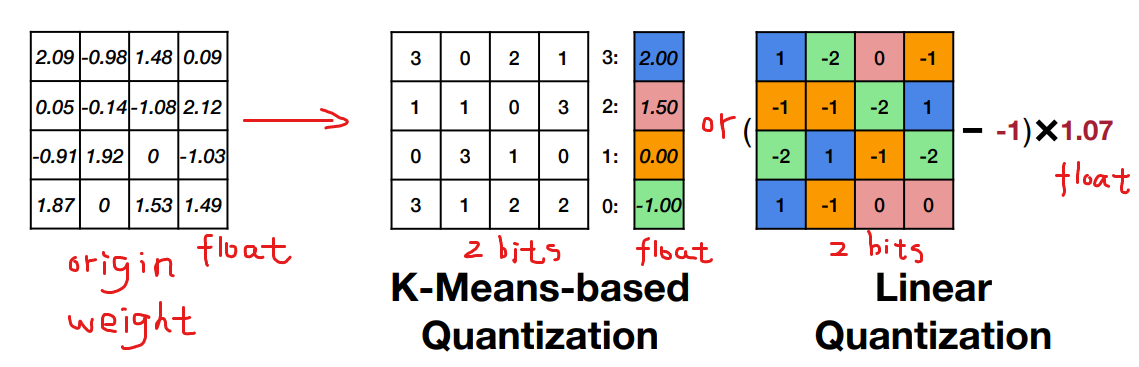
方法：将权重聚类为 $n$ 个类别（使用K-Means聚类算法），其中 $n$ 通常为 $2$ 的某个幂。然后，用每个类别中所有权重的平均值来近似该类别对应的权重。将类别的ID与值的存储在一个编码表（codebook）中，生成一个索引矩阵。

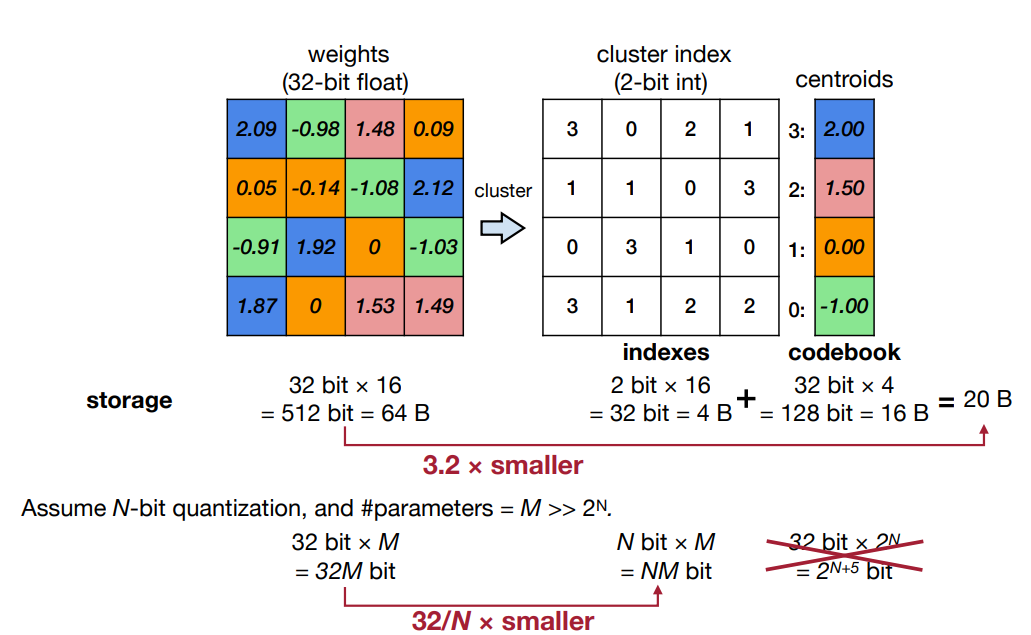
在这里插入图片描述
在存储压缩率方面，设 $N_0$ 为每个权重的原始比特数， $n$ 为用于聚类的个数( $n=2^{N_1}$ )， $M$ 为权重的数量。那么，压缩率约为 $\frac{M*\log_2n + N_0*n}{M*N_0}$ 。一般来说，随着模型规模的增大（即 $M\rightarrow\infty$ ），压缩率接近 $\frac{log_2n}{N_0}$ 。

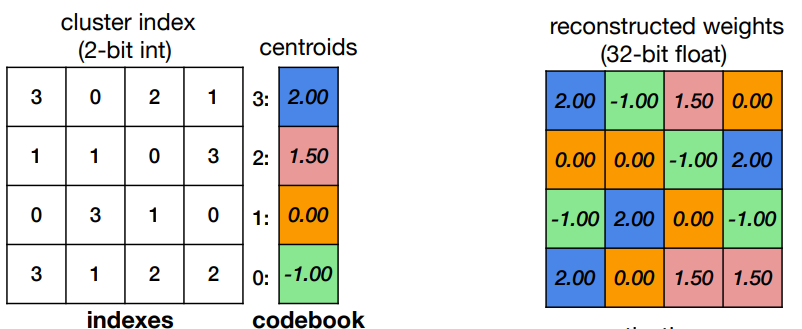
在推理过程中，要根据编码表（codebook）将索引矩阵中的类别id替换成它们所代表的权重，才可进行正常的浮点运算。

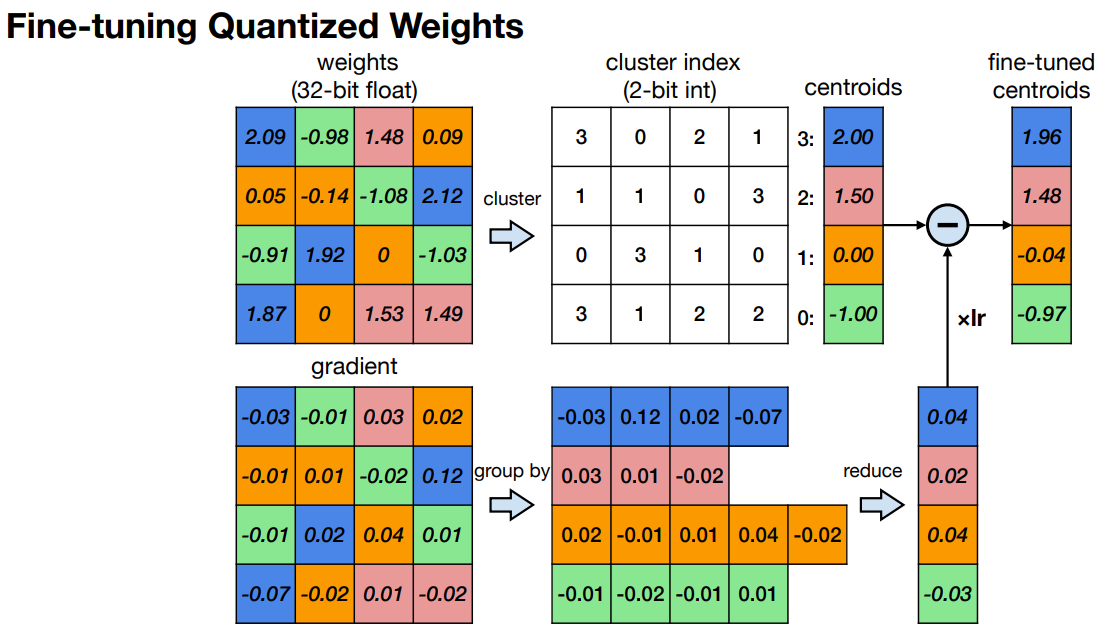
在这里插入图片描述
如果你想对模型进行微调，那么你只需执行梯度下降，参数为编码表条目。一般来说，将每个类别中每个权重的梯度聚合（sum、mean），就可以得到整个类别的梯度，进而可以更新编码表条目。

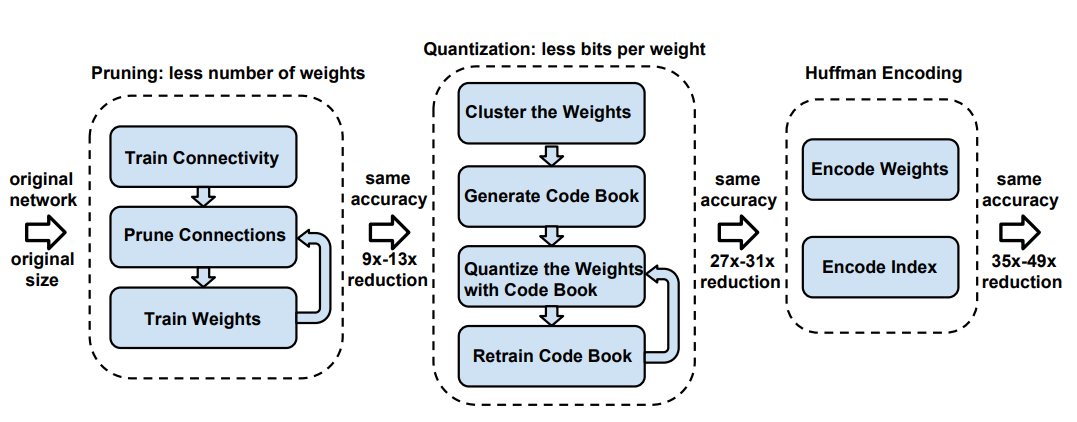
另一个需要注意的是，如果你想同时对一个模型进行修剪和量化，一般的做法是先修剪，后量化。

挑战极限

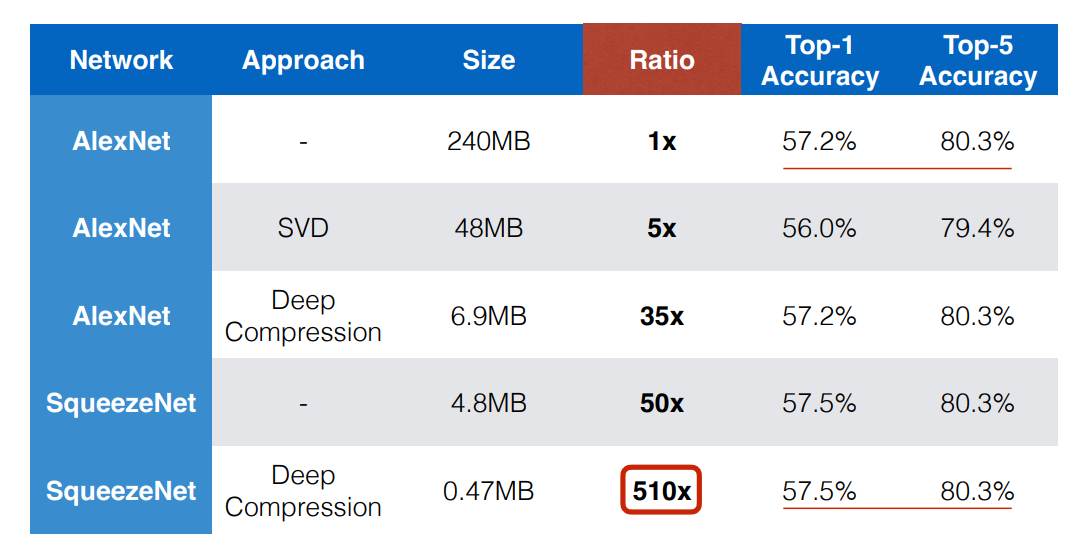
超参数选择：唯一需要选择的超参数是编码簿（codebook）条目的数量，一般来说，标准做法是使用16个；AlexNet的实验表明，卷积层需要4位，全连接层需要2位，才会出现明显的准确性下降。奇怪的是，这些阈值与模型是否先被修剪无关。

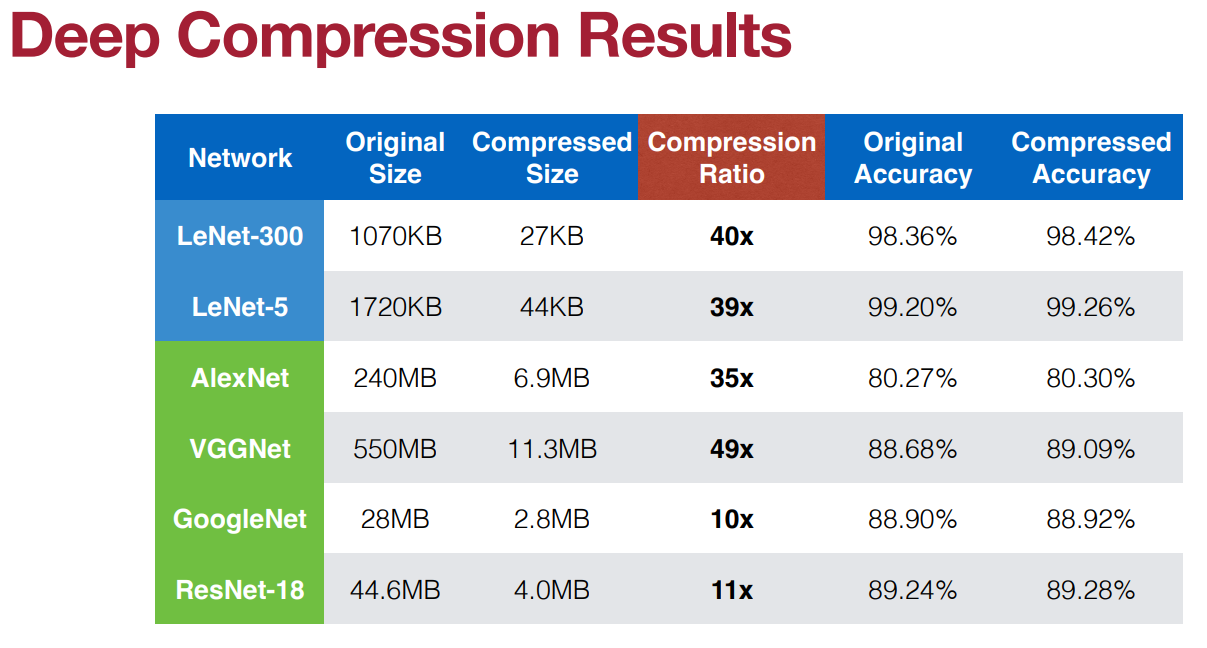
在这里插入图片描述

SqueezeNet：一般来说，人们会问：为什么我们不一开始就训练压缩模型？SqueezeNet的创造者们决定试一试。再加上剪枝和量化，该模型取得了510倍的可笑的压缩率，同时保持了AlexNet的Top-1和Top-5的准确值。

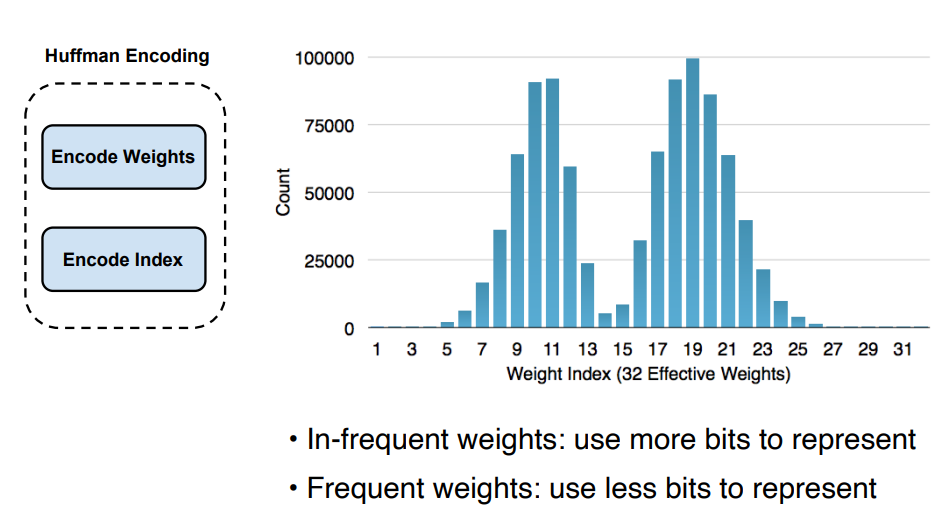
在这里插入图片描述

哈夫曼编码：我们做了一个隐含的假设，即所有的类别索引id都必须由相同数量的比特来表示。但是，很明显，有些类别索引id会比其他的使用更加频繁。为什么我们不对使用更频繁的类别索引id使用较少的比特呢？使用哈夫曼编码就可以做到这一点，并且可以进一步提高压缩率。

在这里插入图片描述
深度压缩 (Deep Compression)
Deep Compression: Compressing Deep Neural Networks With Pruning, Trained Quantization And Huffman Coding

实现

安装需要的库

!pip install torchprofile
!pip install fast-pytorch-kmeans

一个 $n$ 位的k-means量化将把权重分成 $2^n$ 个类别，同一类别中的权重将共享相同的权重值。因此，k-means量化将创建一个codebook，其中包括

centroidsc： $2^n$ fp32聚类中心。
labels：一个 $n$ 位的整数张量，与原始fp32权重张量的元素个数相同。每个整数表示它属于哪个簇。

在推理过程中，根据codebook生成一个fp32张量。

quantized_weight = codebook.centroids[codebook.labels].view_as(weight)

from collections import namedtuple
from fast_pytorch_kmeans import KMeans

Codebook = namedtuple('Codebook', ['centroids', 'labels'])


def k_means_quantize(fp32_tensor: torch.Tensor, bitwidth=4, codebook=None):
    """
    quantize tensor using k-means clustering
    :param fp32_tensor:
    :param bitwidth: [int] quantization bit width, default=4
    :param codebook: [Codebook] (the cluster centroids, the cluster label tensor)
    :return:
        [Codebook = (centroids, labels)]
            centroids: [torch.(cuda.)FloatTensor] the cluster centroids
            labels: [torch.(cuda.)LongTensor] cluster label tensor
    """
    if codebook is None:
        # get number of clusters based on the quantization precision
        n_clusters = 1 << bitwidth
        # use k-means to get the quantization centroids
        kmeans = KMeans(n_clusters=n_clusters, mode='euclidean', verbose=0)
        labels = kmeans.fit_predict(fp32_tensor.view(-1, 1)).to(torch.long)
        centroids = kmeans.centroids.to(torch.float).view(-1)
        codebook = Codebook(centroids, labels)
    # decode the codebook into k-means quantized tensor for inference
    quantized_tensor = codebook.centroids[codebook.labels]
    fp32_tensor.set_(quantized_tensor.view_as(fp32_tensor))
    return codebook

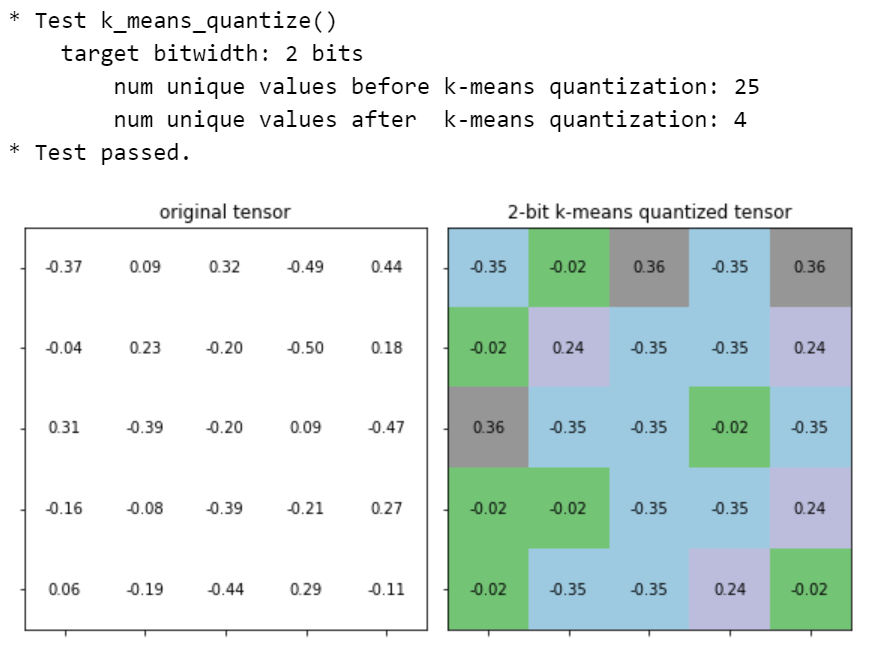
在这里插入图片描述
现在将k-means量化函数包装成一个用于量化整个模型的类。在 "KMeansQuantizer "类中，我们必须保持codebook（即 "中心点 "和 “标签”）的记录，这样我们就可以在模型权重改变时应用或更新codebook。

from torch.nn import parameter
class KMeansQuantizer:
    def __init__(self, model : nn.Module, bitwidth=4):
        self.codebook = KMeansQuantizer.quantize(model, bitwidth)
    
    @torch.no_grad()
    def apply(self, model, update_centroids):
        for name, param in model.named_parameters():
            if name in self.codebook:
                if update_centroids:
                    update_codebook(param, codebook=self.codebook[name])
                self.codebook[name] = k_means_quantize(
                    param, codebook=self.codebook[name])

    @staticmethod
    @torch.no_grad()
    def quantize(model: nn.Module, bitwidth=4):
        codebook = dict()
        if isinstance(bitwidth, dict):
            for name, param in model.named_parameters():
                if name in bitwidth:
                    codebook[name] = k_means_quantize(param, bitwidth=bitwidth[name])
        else:
            for name, param in model.named_parameters():
                if param.dim() > 1:
                    codebook[name] = k_means_quantize(param, bitwidth=bitwidth)
        return codebook

对模型进行量化

bitwidth = 8
quantizer = KMeansQuantizer(model, bitwidth)

当模型量化到较低的比特时，准确率明显下降。因此，我们必须进行训练以恢复准确性。在k-means量化感知训练期间，中心点也会被更新，中心点的梯度计算如下。

$\frac{\partial \mathcal{L} }{\partial C_k} = \sum_{j} \frac{\partial \mathcal{L} }{\partial W_{j}} \frac{\partial W_{j} }{\partial C_k} = \sum_{j} \frac{\partial \mathcal{L} }{\partial W_{j}} \mathbf{1}(I_{j}=k)$

其中 $\mathcal{L}$ 是损失， $C_k$ 是k个中心点， $I_{j}$ 是权重 $W_{j}$ 的标签。 $\mathbf{1}()$ 是指标函数， $\mathbf{1}(I_{j}=k)$ 意味着 $1\;\mathrm{if}\;I_{j}=k\;\mathrm{else}\;0$ ，即， $I_{j}==k$ 。

为了简单起见，我们直接根据最新的权重更新中心点

$C_k = \frac{\sum_{j}W_{j}\mathbf{1}(I_{j}=k)}{\sum_{j}\mathbf{1}(I_{j}=k)}$

def update_codebook(fp32_tensor: torch.Tensor, codebook: Codebook):
    """
    update the centroids in the codebook using updated fp32_tensor
    :param fp32_tensor: [torch.(cuda.)Tensor] 
    :param codebook: [Codebook] (the cluster centroids, the cluster label tensor)
    """
    n_clusters = codebook.centroids.numel()
    fp32_tensor = fp32_tensor.view(-1)
    for k in range(n_clusters):
        codebook.centroids[k] = fp32_tensor[codebook.labels == k].mean()

训练

accuracy_drop_threshold = 0.5
quantizers_before_finetune = copy.deepcopy(quantizers)
quantizers_after_finetune = quantizers

for bitwidth in [8, 4, 2]:
    recover_model()
    quantizer = quantizers[bitwidth]
    print(f'k-means quantizing model into {bitwidth} bits')
    quantizer.apply(model, update_centroids=False)
    quantized_model_size = get_model_size(model, bitwidth)
    print(f"    {bitwidth}-bit k-means quantized model has size={quantized_model_size/MiB:.2f} MiB")
    quantized_model_accuracy = evaluate(model, dataloader['test'])
    print(f"    {bitwidth}-bit k-means quantized model has accuracy={quantized_model_accuracy:.2f}% before quantization-aware training ")
    accuracy_drop = fp32_model_accuracy - quantized_model_accuracy
    if accuracy_drop > accuracy_drop_threshold:
        print(f"        Quantization-aware training due to accuracy drop={accuracy_drop:.2f}% is larger than threshold={accuracy_drop_threshold:.2f}%")
        num_finetune_epochs = 5
        optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
        scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, num_finetune_epochs)
        criterion = nn.CrossEntropyLoss()
        best_accuracy = 0
        epoch = num_finetune_epochs
        while accuracy_drop > accuracy_drop_threshold and epoch > 0:
            train(model, dataloader['train'], criterion, optimizer, scheduler,
                  callbacks=[lambda: quantizer.apply(model, update_centroids=True)])
            model_accuracy = evaluate(model, dataloader['test'])
            is_best = model_accuracy > best_accuracy
            best_accuracy = max(model_accuracy, best_accuracy)
            print(f'        Epoch {num_finetune_epochs-epoch} Accuracy {model_accuracy:.2f}% / Best Accuracy: {best_accuracy:.2f}%')
            accuracy_drop = fp32_model_accuracy - best_accuracy
            epoch -= 1
    else:
        print(f"        No need for quantization-aware training since accuracy drop={accuracy_drop:.2f}% is smaller than threshold={accuracy_drop_threshold:.2f}%")

结果

k-means quantizing model into 8 bits
    8-bit k-means quantized model has size=8.80 MiB
    8-bit k-means quantized model has accuracy=92.75% before quantization-aware training 
        No need for quantization-aware training since accuracy drop=0.20% is smaller than threshold=0.50%
k-means quantizing model into 4 bits
    4-bit k-means quantized model has size=4.40 MiB
    4-bit k-means quantized model has accuracy=84.01% before quantization-aware training 
        Quantization-aware training due to accuracy drop=8.94% is larger than threshold=0.50%
        Epoch 0 Accuracy 92.29% / Best Accuracy: 92.29%
        Epoch 1 Accuracy 92.47% / Best Accuracy: 92.47%
k-means quantizing model into 2 bits
    2-bit k-means quantized model has size=2.20 MiB
    2-bit k-means quantized model has accuracy=12.26% before quantization-aware training 
        Quantization-aware training due to accuracy drop=80.69% is larger than threshold=0.50%
        Epoch 0 Accuracy 90.29% / Best Accuracy: 90.29%
        Epoch 1 Accuracy 91.06% / Best Accuracy: 91.06%
        Epoch 2 Accuracy 91.22% / Best Accuracy: 91.22%
        Epoch 3 Accuracy 91.44% / Best Accuracy: 91.44%
        Epoch 4 Accuracy 91.33% / Best Accuracy: 91.44%