题目来源
122. 买卖股票的最佳时机 II

暴力递归

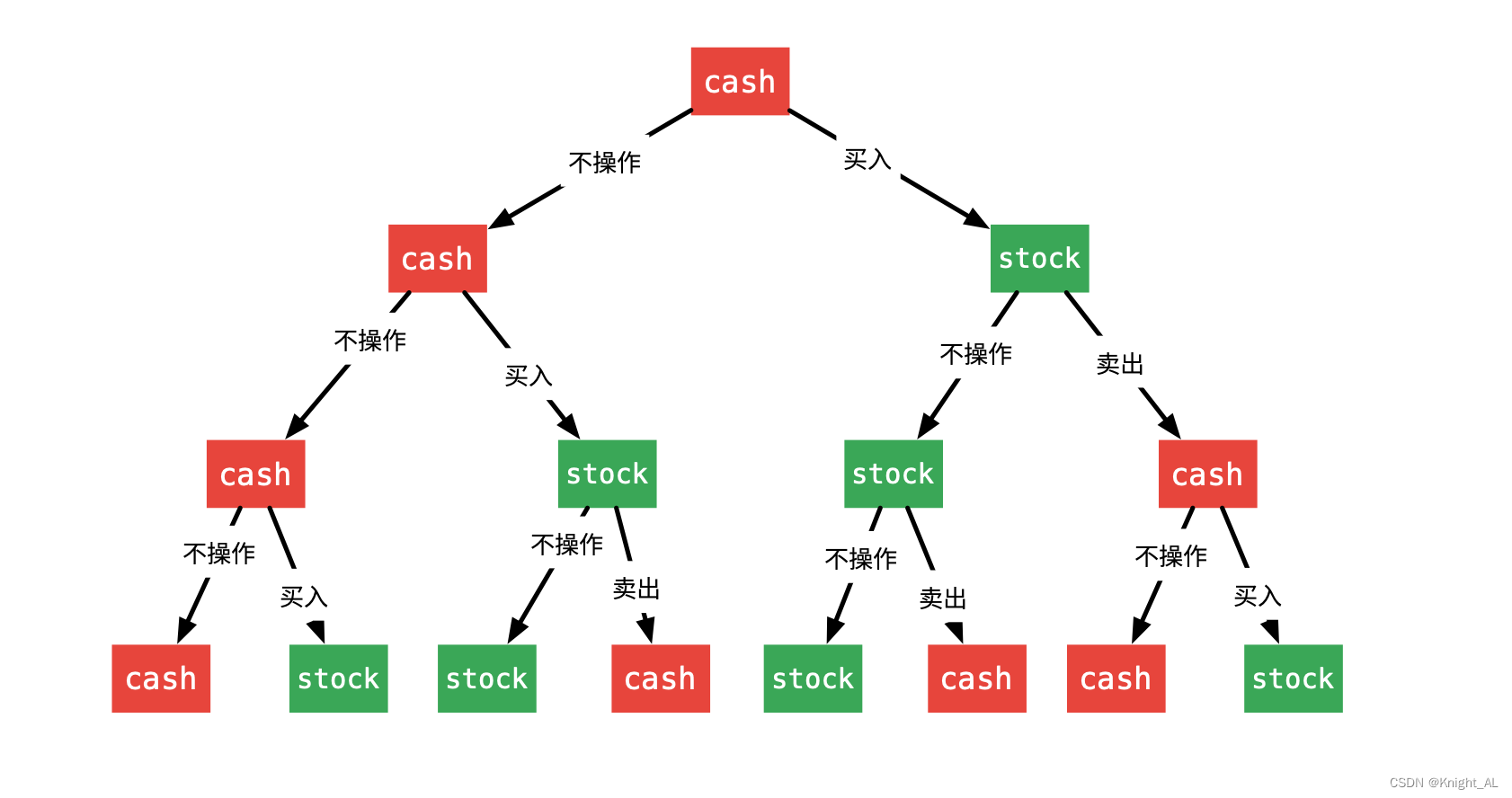
根据题意：由于不限制交易次数，在每一天，就可以根据当前是否持有股票选择相应的操作。「暴力搜索」在树形问题里也叫「回溯搜索」、「回溯法」。
首先画出树形图，然后编码。

class Solution {
    public int maxProfit(int[] prices){
        int len = prices.length;
        if (len < 2){
            return 0;
        }
        return process(prices,0,0);

    }

    //prices数组
    //index索引，从0开始
    //status持有状态。0不持有，1持有
    private int process(int[] prices, int index, int status) {
        if (index == prices.length){  //当索引越界，直接返回0
            return 0;
        }
        int max;
        if (status == 0){  //表示不持有状态
            int p1 = process(prices,index+1,1)-prices[index];  //买票，状态变成持有
            int p2 = process(prices,index+1,0);   //不买票，继续不持有
            max = Math.max(p1, p2);
        }else {  //表示持有状态
            int p1 = process(prices,index+1,0)+prices[index];   //卖票，状态变成不持有
            int p2 = process(prices,index+1,1);  //不卖票，继续持有
            max = Math.max(p1, p2);
        }
        return max;
    }

}

动态规划

直接暴力递归改动态规划

1.process函数直接改成dp
2.dp定义数组是需要看process函数有几个参数要变化(如果process函数有一个参数变化就是定义一维数组)
3.动态规划的返回值是process函数的返回值

class Solution {
    public int maxProfit(int[] prices){
        int len = prices.length;
        if (len < 2){
            return 0;
        }
        int[][] dp = new int[len+1][2];
        for (int i = len-1; i>=0; i--) {
            dp[i][0] = Math.max(dp[i+1][1]-prices[i], dp[i+1][0]);
            dp[i][1] = Math.max(dp[i+1][0]+prices[i], dp[i+1][1]);
        }
        return dp[0][0];
    }
}

贪心

首先买卖股票一定得是赚钱的，也就是说我们的利润一定的是正数，所以此时我们只用遍历一次数组，将每天的差值记录下来，只取正数之和就是最后的答案，下面
举一个例子：

• 数组[7,1,2,5,3,2,6,4]，此时我们根据题意很容易可以得到，如果我们在第二天，即股票价格为1的时候买入，在第四天，即股票价格为5的时候卖出，我们此时可以赚4。同理，在第六天买入，在第七天卖出，此时赚4，总共赚4 + 4 = 8。
• 我们此时进行分析，我们可以将第二天买入第四天卖出时，赚的钱可以划分为二到三天赚的钱1，加上三到四天赚的钱3，3 + 1 = 4。同理，第六天买入第七天卖出，赚的钱为六到七天赚的钱4，总共赚4 + 4 = 8，我们此时再进行求出该数组各个区间的差值为[-6,1,3,-2,-1,4,-2]，我们很容易发现我们总共赚的钱其实就是区间差值为正值之和。
• 所以我们可以将赚的钱进行区间化，只进行记录差值为正值的值，并进行求和即为最后答案。

代码实现

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length < 2 || prices == null){
            return 0;
        }
        int ans = 0;
        for(int i = 1;i<prices.length;i++){
            ans += Math.max(0,prices[i]-prices[i-1]);
        }
        return ans;
    }
}