欢迎来到繁星的CSDN,本期内容包括快速排序(QuickSort)的递归版本和非递归版本以及优化。

一、快速排序的来历
快速排序又称Hoare排序,由霍尔 (Sir Charles Antony Richard Hoare) ,一位英国计算机科学家发明。霍尔本人是在发现冒泡排序不够快的前提下,发明了快速排序。不像希尔排序等用名字命名排序方法,霍尔直接将其命名为快速排序,但时至今日,快速排序仍然是使用最广泛最稳定的排序算法。
二、快速排序主代码
快速排序是如何实现的呢?私以为思想和二叉树的前序遍历类似。
(没有看过二叉树的看这里:一文带你入门二叉树!-CSDN博客)
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = PartSort1(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}快速排序采用了分治的思想,之前在排序(一)提到过,如果将数组拆成一个个小块再排序,会比一整个数组集体排序来的快。快排也正是利用这一点,从零到整地排序整个数组,并确定好分拆端点的最终位置,使得每一组的排序结束都是最终位置,无需再调整。而由于不知道数组需要被拆分成几块,类似于二叉树的递归遍历,快排也需要递归来帮助拆分和子数组排序。
下面阐述PartSort1这个函数是如何进行单趟排序的了。
三、快速排序(递归版单趟排序)
Part1 Hoare法
先上动图:

可以注意到,PartSort的参数是数组a,数组最左端元素的下标left,最右端元素的下标right。
key就是子数组(即left~right范围内)的第一个元素。
整个流程如下:
1、right向左遍历,直到找到一个小于key的值,停下。
2、left向右遍历,直到找到一个大于key的值,停下。
3、两者交换。
4、重复上述流程,直到left与right相遇,交换key和最后相遇处的下标mid。
5、随后返回mid,并利用mid继续将[left,right]区间分割为[left,mid-1]和[mid+1,right]区间,当不能分割的时候,该数组排序完毕。
问题讲解
如何确保key交换后所在的位置就是最终位置?
首先,从一个升序数组来看,对于其中任何一个元素(除首尾两个),该元素左侧均更小,右侧均更大。换句话说,保证左侧比key元素更小,右侧比key元素更大,即得到了这一元素的位置。
不难发现,被left遍历过的地址都是比key小的,被right遍历过的地址都是比key大的,因为如有left发现比key大,或者right发现比key小,都已进行过交换。
唯一需要判定的,就是最后一个元素是否比key小。
(1)left遇到right
当right停下,说明right所处位置的元素应该比key小。
那么left撞到right的时候,一定是right所处的位置,保证了该位置比key小。
(2)right遇到left
当left停下,说明已经交换完毕,此时left所处位置的元素比key小。
两种情况本质相同,都是保证了停下的那一方所处位置比key小。
int PartSort1(int* arr, int begin, int end)
{
int left = begin, right = end;
int key = begin;
while (left < right)
{
//left<right防止越界
//使用>=而不是>防止数据出现死循环
while (left < right && arr[right] >= arr[key])
//寻找比key小的值
{
right--;
}
while (left < right && arr[left] <= arr[key])
//寻找比key大的值
{
left++;
}
swap(&arr[left], &arr[right]);
}
int mid = left;
swap(&arr[key], &arr[mid]);
return mid;
}Part2 挖坑法
先上动图: 
挖坑法和hoare法的差别不大,思路都是将key的位置安排在最终位置后,再分段快排。
但挖坑法的确会比hoare法更加容易理解。
坑的位置就代表相遇位置,每“交换”一次,就将坑位换到被交换的位置,最后坑落在哪里,就将key值填入。
和hoare法不同的是,挖坑法需要多一个临时变量储存key值,在进行操作的时候只需要赋值,而不是swap交换。
int PartSort2(int* a, int left, int right) {
int key = a[left];
int hole = left;
while (left < right) {
while (left < right && a[right] >= key) {
right--;
}
swap(&a[right], &a[hole]);
hole = right;
while (left < right && a[left] <= key) {
left++;
}
swap(&a[left], &a[hole]);
hole = left;
}
int mid = hole;
a[hole] = key;
return mid;
}Part3 双指针法
怎么能够让双指针缺席呢!

本质和前面两种没有区别,只是遍历的方向不同,前两种都是左右两侧开始遍历,而双指针法从一端开始遍历。prev代表比key小的值,cur去遍历,并确保prev的下一个位置上比key大,将较大的元素集体向后驱赶。
int PartSort3(int* a, int left, int right) {
int fast = left;
int slow = left;
int key = a[left];
while (fast <= right) {
if(a[fast] < key)
swap(&a[++slow], &a[fast]);
fast++;
}
swap(&a[slow], &a[left]);
return slow;
}总结
Part123三种办法没有高下之分,都可以作为QuickSort的一部分使用。
可以说QuickSort的代码实现和理解复杂程度并不如之前说的堆排那么抽象,但是性能确实优秀。
四、快速排序(非递归版)
我们知道,递归占据了大量的栈帧空间,尽管市面上大部分编译器已经增强了递归的性能,致使用递归的快排和不用递归的快排时间上差别不大,但递归空间上的占据却不可忽视。快排非递归版应运而生。
这一部分需要用到栈的知识,如果还没看,可以查看:栈和队列的介绍与实现-CSDN博客
非递归版本最重要的是,如何实现数组的分割,与进行多次排序。
利用好之前学过的数据结构,我们可以想起栈与队列,我们用栈来演示。
void QuickSortno(int* a, int left, int right) {
Stack ps;
StackInit(&ps);
StackPush(&ps, left);
StackPush(&ps, right);
while (!StackEmpty(&ps)) {
int end = StackTop(&ps);
StackPop(&ps);
int begin = StackTop(&ps);
StackPop(&ps);
int key=PartSort1(a, begin, end);
if (key + 1 < end) {
StackPush(&ps, key+1);
StackPush(&ps, end);
}
if (key - 1 > begin) {
StackPush(&ps, begin);
StackPush(&ps, key-1);
}
}
StackDestroy(&ps);
}有点像层序遍历,我们将待排序的子数组的两端,放入栈中,每两个为一组弹出并进行单趟排序,排序完毕后,将新增的两个子数组的两端放入栈中。循环往复,便可以得到结果。
本质思想还是一致的。
五、快速排序的优化
快速排序的最坏情况是升序/降序的数组,复杂度都达到了O(n^2)。
经研究表明,问题出在基准值上,也就是每次排序时最左端的数据。如果将基准值改为数组内的随机值,平均情况将比最好情况只糟39%,比只取最左端数据为基准值要好很多。
所以优化的第一个方向在于调整基准值。
三数取中法
int GetMidi(int* a, int left, int right)
{
int midi = (left + right) / 2;
// left midi right
if (a[left] < a[midi])
{
if (a[midi] < a[right])
{
return midi;
}
else if (a[left] < a[right])
{
return right;
}
else
{
return left;
}
}
else // a[left] > a[midi]
{
if (a[midi] > a[right])
{
return midi;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}代码很长,实际作用就是在left,(left+right)/2,right三个数中间取中间数,很好地做了分割。正如之前所述,越能将数组分割为两半,便越可以以更高的效率去排序。
小区间优化
优化的第二个方向在于快排的最后几层递归上。
无论递归多少次,我们都要在最后几层递归上耗费大量的时间与空间(只需要看区间数量,便可以知道需排序的区间呈指数级增长)。
递归是大招,但是更适合大场面,所以我们有以下优化:
if (left >= right)
return;↓
if (right-left<=10)
{
InsertSort(a+left, right - left+1);
return;
}没错,就如排序(一)中提到的,如果数组元素比较少,插入排序的复杂度体现不出来。
这意味着我们可以在这个时候直接使用插入排序(当然希尔排序也是可以的,可为什么不全部都直接用希尔排序呢?)
感受一下优化过的和未优化过的:
优化前:

优化后:
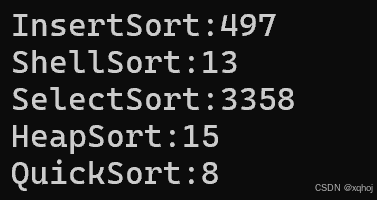
在10w量级的数据里,优化前后效率提升显著,相信量级更大的时候会更体现出优势。
本篇内容到此结束,谢谢大家的观看!
觉得写的还不错的可以点点关注,收藏和赞,一键三连。
我们下期再见~
往期栏目: 排序(一)——冒泡排序、直接插入排序、希尔排序(BubbleSOrt,InsertSort,ShellSort)-CSDN博客