👦个人主页:@Weraphael
✍🏻作者简介:目前是C语言学习者
✈️专栏:【C/C++】算法
🐋 希望大家多多支持,咱一起进步!😁
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注😍
目录
- 一、思想
- 二、运用场景
- 三、分析
- 情况1:mid = (l + r + 1) / 2
- 情况2:mid = (l + r ) / 2
- 四、代码模板及使用条件
- 模板1
- 模板2
- 使用条件
- 五、边界问题分析
- 六、例题
- 1、例题描述
- 2、思路
- 3、代码实现
一、思想
<图片来源于百度>

如上动图所示,若在一个有序的数组中查找一个数,binary_search(二分查找)需要查找三次,而sequential_search(顺序查找)则需要11次。
由此二分的优点是查找次数少,查找速度快,平均性能好并且其时间复杂度O(log(n))
二、运用场景
在一个数组内,若要查找一个数字,要求找到这个元素的下标(开始位置或者结束位置),并且这个数组范围内的元素都具有单调性,因此可以用二分查找法来做。
三、分析
l - 左边界
r - 右边界
n - 元素个数
val - 查找元素
a[] - 原数组
情况1:mid = (l + r + 1) / 2

- 二分范围:
l = 0、r = n - 1,首先二分查找≤val的最右边界 - 当
a[mid] >= val时,说明第一个>=val元素的位置一定在mid处或mid的右侧,即答案的范围:[mid,r],将l更新为mid - 否则当
a[mid] < val时,说明val在mid的左侧(不包括mid),即答案范围:[l,mid - 1],将r更新为mid - 1 - 如果
a[l]!=val说明没有找到该值,否则就找到了。
情况2:mid = (l + r ) / 2

- 二分范围:
l = 0、r = n - 1,首先二分查找≥val的最左边界 - 当
a[mid] >= val时,说明第一个>=val元素的位置一定在mid处或mid的左侧,即答案的范围:[l,mid],将r更新为mid - 否则当
a[mid] < val时,说明val在mid的右侧(不包括mid),即答案范围:[mid+1,r],将l更新为mid + 1 - 如果
a[l]!=val说明没有找到该值,否则就找到了。
四、代码模板及使用条件
模板1
当我们将区间
[l,r]划分成[l,mid]和[mid + 1,r]时,其更新操作是r = mid或者l = mid + 1,计算mid时不需要+1,即mid = (l + r)/2。
int binary_search1(int l, int r)
{
while (l < r)
{
int mid = (l + r) / 2;
if (check(mid)) //检查mid是否满足某种性质
{
r = mid;
}
else
{
l = mid + 1;
}
}
return l;
//由于当 l=r 时 ,while 循环停止,
//因此最后的返回值既可以是 l 也可以是 r
}
模板2
当我们将区间
[l,r]划分成[l,mid - 1] 和[mid,r]时,其更新操作是r = mid - 1或者l = mid,此时为了防止死循环,计算mid时需要 + 1(这属于边界问题,后面有介绍),即mid = (l + r + 1) / 2。
int binary_search2(int l, int r)
{
while (l < r)
{
int mid = (l + r + 1)/ 2;
if (check(mid))//检查mid是否满足某种性质
{
l = mid;
}
else
{
r = mid - 1;
}
}
return l;
//由于当 l=r 时 ,while 循环停止,
//因此最后的返回值既可以是 l 也可以是 r
}
使用条件
假设初始时二分区间为
[l,r],每次二分都会缩小范围,当你发现左边界l要更新为mid时,此时就要用模板2;如果左边界I更新为mid + 1,此时就使用模板1,所以模板的使用条件是根据代码而使用的。
五、边界问题分析
假设模板2中的mid没有+1,此时
mid = (l + r) / 2,就会发生边界问题。例如当 l 和 r 相差1的时候,l + 1 = r时,带入得,mid = (2l + 1) / 2,下取整,mid = l。左边界再次更新为l = mid = l,l更新还是l,就会发生死循环。
六、例题
<牛客网例题,点击跳转>
1、例题描述
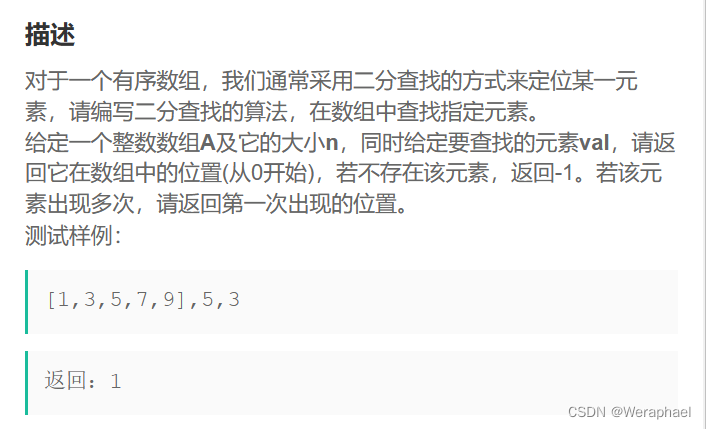
2、思路

用二分查找第一个 >= val 的位置,查找成功则返回下标,否则返回 -1
3、代码实现
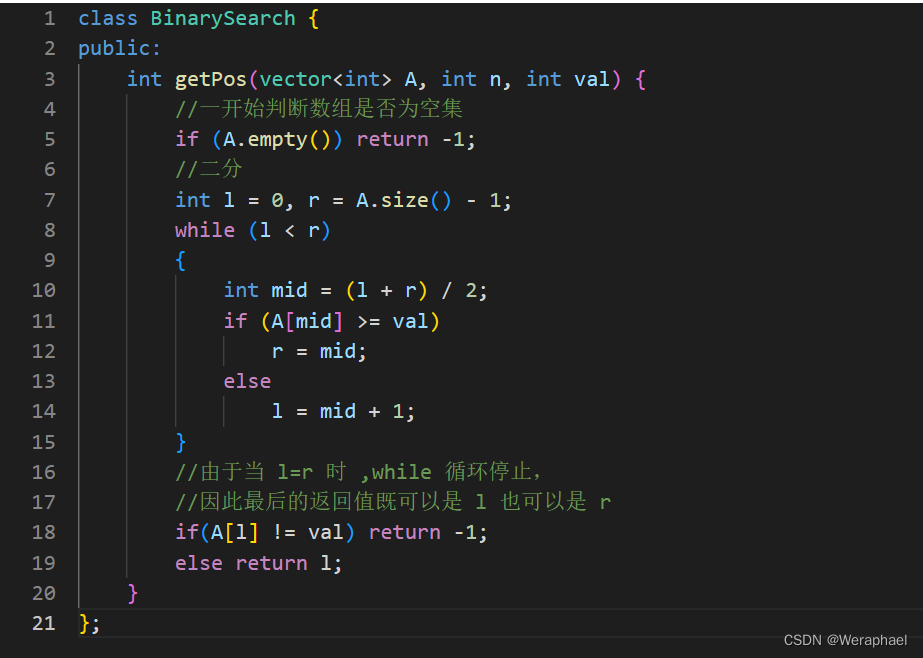
![[golang Web开发] 1.golang web开发简介以及web服务器的搭建以及http协议简介](https://img-blog.csdnimg.cn/27d7c237860b4eb481b5687ea183ff86.png)