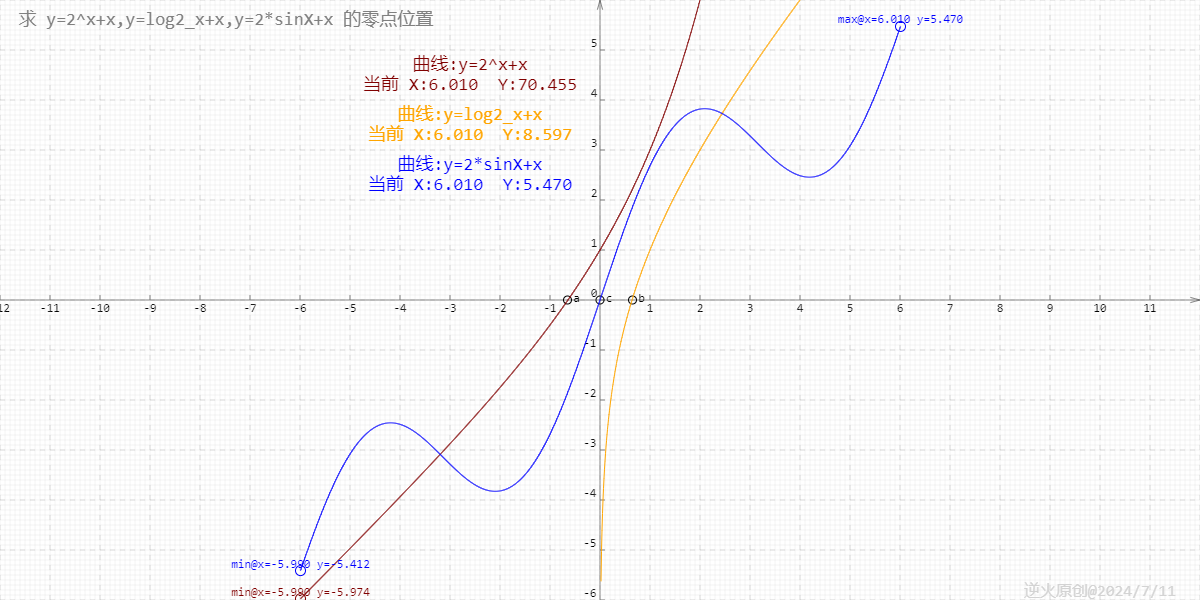
差分约束——AcWing 362. 区间

news2024/11/16 0:01:04

差分约束

定义

差分约束系统是一种在计算机科学和运筹学中用于解决特定类型优化问题的工具。它主要用于处理一类线性不等式组，这些不等式描述了变量之间的相对大小关系，而不是直接的绝对值大小。差分约束系统通常用于路径寻找、调度、资源分配等问题。

运用情况

最短路径问题：在有向图中，如果边的权重表示成本或距离，差分约束可以用来找到从一个源点到其他所有点的最短路径。
任务调度：在任务调度问题中，每个任务可能有完成时间的限制，差分约束可以用来确保任务按照正确的顺序执行，并满足时间限制。
资源分配：当需要在多个项目之间分配有限资源时，差分约束可以用来确保资源分配的公平性和效率。

注意事项

环路检测：在构建差分约束图时，必须注意避免形成负权环，因为这将导致解决方案不存在或无穷大。
松弛变量：有时，引入松弛变量可以使问题更容易求解，但这也可能增加问题的复杂度。
精度问题：在使用浮点数进行计算时，要注意数值精度可能导致的误差。

解题思路

构建图模型：将差分约束转换为有向图中的边，其中顶点代表变量，边的权重代表差分约束中的常数。
应用最短路径算法：利用如贝尔曼-福特算法或迪杰斯特拉算法等最短路径算法来求解。贝尔曼-福特算法尤其适用于存在负权边的情况。
检查环路：在求解过程中，要检查是否存在负权环，如果有，则说明问题无解。
解析结果：根据最短路径算法的结果，解析出原始问题的解。

AcWing 362. 区间

题目描述

362. 区间 - AcWing题库

运行代码

#include <cstring>
#include <iostream>

using namespace std;

const int N = 50010, M = N * 3 + 10;

int n;
int h[N], e[M], ne[M], w[M], idx;
int q[N], dist[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void spfa()
{
    memset(dist, -0x3f, sizeof dist);
    q[0] = 0, dist[0] = 0, st[0] = true;
    
    int hh = 0, tt = 1;
    while(hh != tt)
    {
        int t = q[hh ++ ];
        if(hh == N) hh = 0;
        st[t] = false;
        
        for(int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if(dist[j] < dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if(!st[j])
                {
                    q[tt ++ ] = j;
                    if(tt == N) tt = 0;
                    st[j] = true;
                }
            }
        }
    }
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h);
    for(int i = 1; i < N; i ++ )
    {
        add(i, i - 1, -1);
        add(i - 1, i, 0);
    }
    
    for(int i = 0; i < n; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        a ++, b ++;
        add(a - 1, b, c);
    }
    
    spfa();
    
    cout << dist[50001] << endl;
    
    return 0;
}