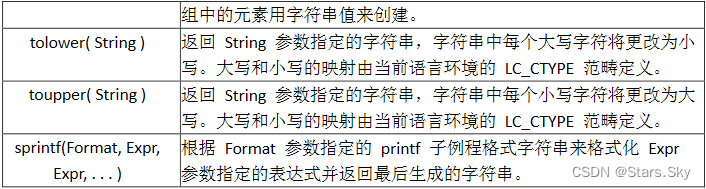
实验名称:基于激光相位分立调制的多波长干涉相位同步解调方法研究
研究方向:激光测量
测试目的:
在长度测量中,绝对距离测量(ADM)可实现高精度、大范围和瞬时距离测量,与相对位移测量(RDM)相比,不需要对干涉条纹进行连续计数即可实现精密测量,广泛应用于高端装备制造、大尺寸机械零部件的检测和飞机装配等领域。多波长干涉测量法是一种最基本的,也是应用最为广泛的绝对距离测量方法,其中多波长对应干涉相位的精确解调是最为关键的问题之一。
测试设备:ATA-2082高压放大器、激光器、半波片、分光镜、迈克尔逊干涉仪、测量角锥棱镜、纳米定位线性平台、非接触式电容式传感器、反射镜、光电探测器。

图:FDM双波长干涉光路实验装置
实验过程:
以FDM双波长干涉相位同步解调方法为例,对其进行了仿真分析及实验验证。搭建了所提出的FDM双波长干涉测量光路,进行了系统稳定性实验、纳米级位移测量实验、纳米级步进非线性误差实验、两位位移解调同步性实验、动态相位解调实验。
由于侧重于研究多波长干涉相位解调的性能,所以采用两个自由空间的频率稳定He-Ne激光器(632.991nm,633.429nm),主要通过纳米位移测量等实验分析相位解调的精度和非线性误差。光路中采用两个半波片(HWP)使激光光束的偏振方向与EOM的光轴(EO-PM-NR-C1,Thorlabs)成45°。采用两个EOM对两束激光以不同频率进行相位调制后在分光镜(BS)处合光。在迈克尔逊干涉仪中,测量角锥棱镜(M2)安装在纳米定位线性平台上。采用非接触式电容式传感器测量,线性平台具有亚纳米级分辨率和±1nm的可重复性,闭环行程范围和线性误差分别为15μm和0.03%。FDM干涉激光信号被反射镜(R2)反射后由光电探测器探测。使用定制的基于FPGA的ADC&DAC开发板进行信号处理,包括生成相位调制信号,获取FDM干涉信号和解调干涉相位。产生的相位调制信号由双通道高压放大器(ATA-2082,Aigtek)放大后用来驱动电光调制器EOM。相位调制信号和低通滤波器的设置与模拟信号相同(ω1=146kHz,ω2=195kHz,ωt=100Hz,ωL=49kHz)。通过调整高压放大器的放大倍数,将两个EOM的正弦相位调制深度均设置为约2rad。
1、稳定性实验
为了测试FDM干涉相位同步解调系统在测量镜M2静止时,环境因素对两路相位解调结果的影响,对EOM施加正弦加三角波复合调制,同时记录两路干涉信号解调相位的变化情况。实验结果如图2所示。
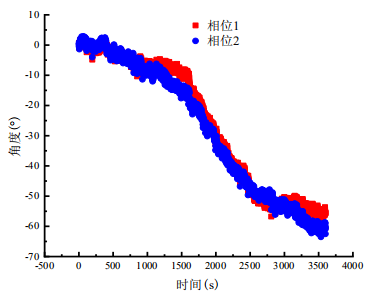
图2:稳定性实验结果
从图2中可以看出:在1个小时内两路相位变化约为70°,每分钟约变化1.2°,对于干涉信号相位解调实验,一般能够在毫秒级时间内完成,上述目标漂移对多波长干涉测量结果的影响可忽略不计。
2、步进测量实验
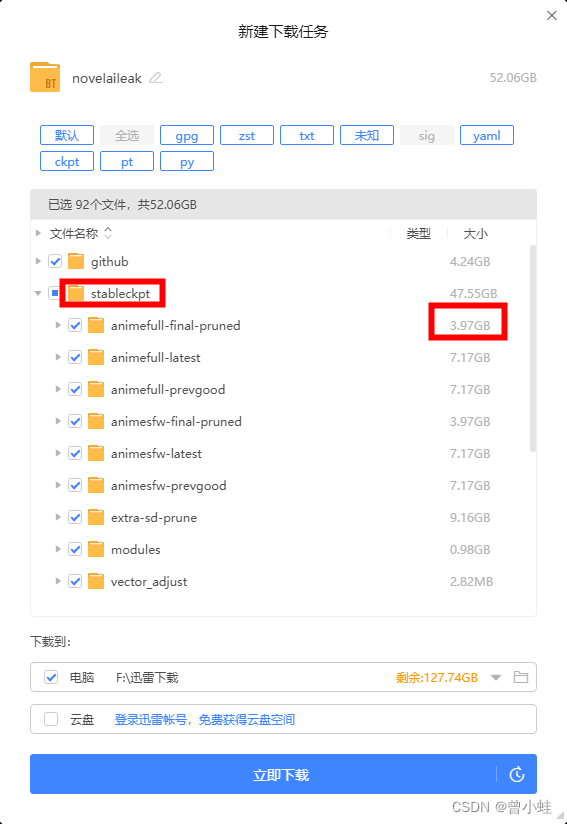
为了测试FDM双波长干涉相位同步解调系统在纳米级范围内位移测量精度。在实验开始之前,先对光路进行微调,以保证光电检测器能够接收到正常的干涉信号。接着调节光电检测器的增益旋钮,以将位移测量信号的强度调至适当的大小。将测量镜安装在行程为15μm,重复定位精度为±1nm的P-753.1CD精密线性促动器上,从0开始使其以10nm的步长步进,步进到1μm,共100个点,导轨的步进速度设置为1μm/s。PC控制软件对实验过程中的解调位移和P-753.1CD精密线性促动器的位置进行了同步记录。实验结果如图3、图4所示。
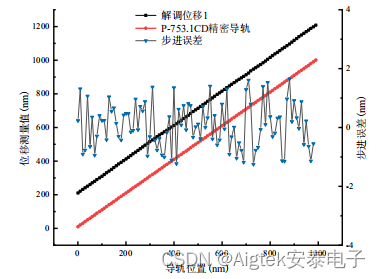
图3:第一路步进实验结果
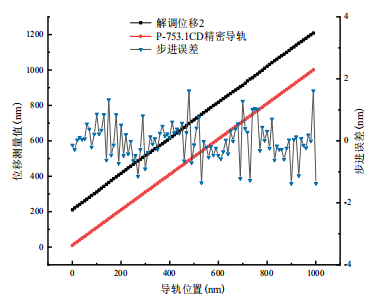
图4:第二路步进实验结果
为了清晰地观察,位移测量数据分别向上平移2μm。研制系统的线性位移测量数据与P-753.1CD精密线性促动器的定位数据间的最大偏差分别为1.64nm、1.61nm,两者都在±2nm范围内,标准偏差分别为0.81nm、0.75nm,均在1nm范围之内,说明FDM双波长干涉相位同步解调系统能够实现纳米级的测量精度。
3、非线性误差测量实验
为了测试FDM双波长干涉相位同步解调系统非线性误差的大小,将测量镜安装在行程为15μm,重复定位精度为±1nm的P-753.1CD精密线性促动器上,从0开始使其以10nm的步长步进,步进到3μm,共300个点,导轨的步进速度设置为1μm/s。每一次步进,实时的导轨位置和解调位移值是被同时记录的,直到测量结束,两路位移解调的结果如图5、图6所示,其中图5(a)、图6(a)表示系统所解调的位移测量值、精密导轨的位置以及每次步进的误差值,图5(b)、图6(b)是误差值的FFT分析结果。
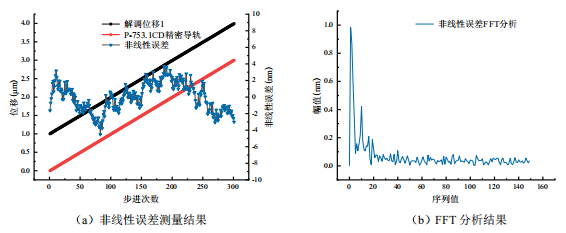
图5:第一路非线性误差测量和FFT分析结果
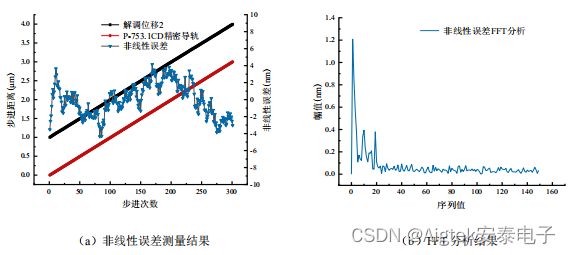
图6:第二路非线性误差测量和FFT分析结果
由于外部环境的变化,如温度、CO2浓度等,此外P-753.1CD的运动方向与光束的方向也有一定的角度偏差,这些都使得位移解调结果具有线性误差,但不是非线性误差的范畴。所以图5和图6中表示的是去除了线性误差之后的位移误差。由于相位解调算法中的反正切操作,可能会引入周期为π的非线性误差,因此如果相位解调出现非线性误差,则会在二次谐波分量出现一个峰值。但是在图5和图6所示位移偏差的FFT分析中,二次谐波分量处两个位移偏差的非线性误差均小于0.3nm。在一阶条纹(周期为2π)处的0.6nm的较大非线性误差,是由实验设置中PBS的偏振泄漏引入,而不是由相位解调系统引起,说明了FDM双波长干涉相位同步解调系统具有较小的非线性误差。
4、两路位移解调同步性实验
为了测试FDM双波长干涉相位同步解调系统中两路相位解调的一致性。将测量镜安装在行程为15μm,重复定位精度为±1nm的P-753.1CD精密线性促动器上,从0开始使其以10nm的步长步进,步进到500nm,共50个点,导轨的步进速度设置为1μm/s。每一次步进,实时的导轨位置和解调位移值被同时记录,直到测量结束,两路位移解调的结果及其差值如图7所示。
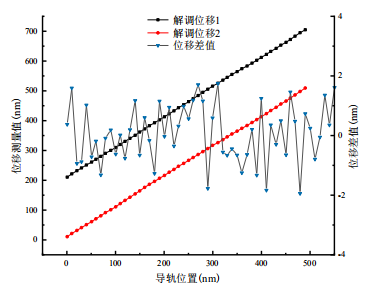
图7:两路相位解调同步性实验
为了清晰地观察,第一路的位移测量数据向上平移200nm。图中可以清晰看出,两路解调位移偏差在±2nm范围内,证明了FDM双波长干涉相位解调系统中的两路位移解调具有良好的同步性。
5、动态相位解调实验
为了测试系统动态相位同步检测的性能,实施了双路的动态相位解调实验。对于动态目标,总谐波失真(THD)为所有谐波的等效均方根(RMS)幅度与基频幅度的比值,用于评估相位解调的非线性。由于THD分析要求输入是单频信号,因此施加正弦电压以使测量镜M2以30Hz的频率在7rad的动态范围内运动。以10kHz的速率同时记录两个解调相位,如图8所示。根据图9所示的THD分析结果,检测到的相位1和相位2的基频分别为29.91Hz和29.99Hz,THD分别为7.65%和7.70%,信噪比(SINAD)均为21.64dB,证明了所提出的动态相位同步检测方案的可行性。
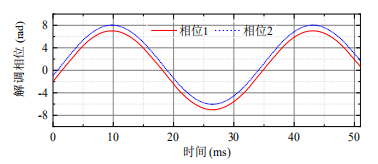
图8:两路正弦相位解调结果
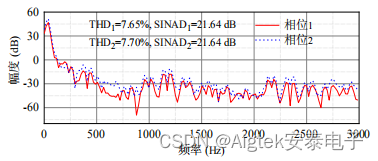
图9:THD分析结果
实验结果:
在FDM双波长干涉相位同步解调系统验证实验中:系统稳定性实验结果良好,具备所需要的测量实验条件;在纳米位移测量实验中,最大的步进误差不超过±2nm,而标准偏差不大于1nm;通过纳米级的非线性误差测量实验,证明了该方法的非线性误差较小,在0.4nm以下;两路位移解调同步性实验中,两路实时解调位移差值在±2nm范围内,验证了两路相位解调具有较高的同步性;动态相位解调实验中,施加线性变化的正弦电压使测量镜以30Hz的频率在7rad的动态范围进行移动,以10kHz的速率同时记录两个解调相位,检测到的相位1和相位2的基频分别为29.91Hz和29.99Hz,THD分别为7.65%和7.70%,SINAD均为21.64dB。通过上述实验,验证了FDM双波长干涉相位解调系统具有良好的性能。
安泰ATA-2082高压放大器:

图:ATA-2082高压放大器指标参数