支持向量机（support vector machines, SVM）是一种二分类模型。基本模型是定义在特征空间上的间隔最大的线性分类器；学习策略：间隔最大化；学习算法：求解凸二次规划的最优化算法。

支持向量机分为线性可分支持向量机（linear support vector machine in linearly separable case）、线性支持向量机（linear support vector machine）、非线性支持向量机（non-linear support vector machine）。

$n$ 维空间的超平面 $({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=0$，其中 $\mathbf{w},\mathbf{x}\in {\mathbb{R}}^n)$ :

• 超平面方程不唯一
• 法向量 $\mathbf{w}$ 和位移项 $b$ 确定一个唯一超平面
• 法向量 $\mathbf{w}$ 垂直于超平面（缩放 $\mathbf{w},b$ 时, 若缩放倍数为负数会改变法向量方向)
• 法向量 $\mathbf{w}$ 指向的那一半空间为正空间，另一半为负空间
• 任意点 $\mathbf{x}$ 到超平面的距离公式为

$$r=\frac{\left|{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right|}{\Vert \mathbf{w}\Vert }$$

• 若存在一个划分样本类别的超平面，则存在无数个可划分的超平面。

线性可分支持向量机

如下图所示，分类目标是将两类样本分开。

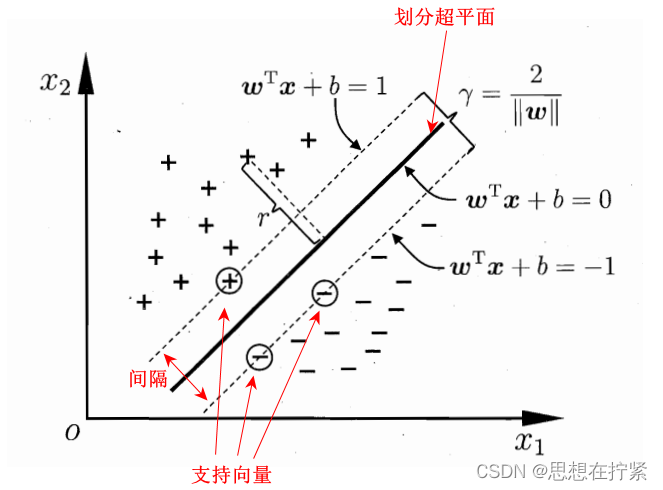
二分类问题中，划分超平面应满足（以下条件可扩充至高维的情形）：

1. 能正确划分两类样本
2. 过「支持向量」且平行于「划分超平面」的两个超平面距离最大（间隔最大）
3. 距所有「支持向量」距离相等

数学模型

根据划分超平面的满足条件，推导支持向量机的数学模型。

定义数据及标签

给定训练数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } D=\left\{\left(\boldsymbol {x_1}, y_1\right),\left(\boldsymbol {x_2}, y_2\right), \ldots,\left(\boldsymbol {x_m}, y_m\right)\right\} D={(x1​,y1​),(x2​,y2​),…,(xm​,ym​)}，共有两类标签 y i ∈ { − 1 , + 1 } y_i \in\{-1,+1\} yi​∈{−1,+1}，$y_i=-1$ 为反例，$y_i=+1$ 为正例。

划分超平面的线性模型

划分超平面线性模型：${\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b=0$。其中，$\mathbf{w}={\left(w_1,w_2,\dots ,w_d\right)}^{\mathrm{T}}$ 为法向量，决定超平面的方向；$b$ 为偏移项，决定超平面与原点间的距离。划分超平面可简记为 $\left(\mathbf{w},b\right)$。

正确线性划分

假设超平面 $(\mathbf{w},b)$ 能将训练样本正确分类，

从划分超平面来看，对于 $\left({\mathbf{x}}_i,y_i\right)\in D$，若 $y_i=$ $+1$，则有 ${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩾0$；若 $y_i=-1$, 则有 ${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b<0$。简写为：
$$y_i[{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b]⩾0\text{\hspace{1em}(1)}$$
从穿过「支持向量」且平行于「划分超平面」的两个超平面来看，对于 $\left({\mathbf{x}}_i,y_i\right)\in D$，若 $y_i=+1$，则有${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩾+1$；

若 $y_i=-1$，则有 ${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩽-1$。简写为：
$$y_i[{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b]⩾1\text{\hspace{1em}(2)}$$
确定划分超平面时只有支持向量起作用，其他样本点不起作用。如果移动支持向量将改变所求的解；但移动、去掉其他样本点，解不会改变，因此采用公式 (2) 来表示正确线性划分更好。

间隔最大

从两类支持向量所在超平面间的距离或支持向量到划分超平面的距离*2两个角度，可得异类支持向量到划分超平面的距离和为：
$$\gamma =\frac{2}{||\mathbf{w}||}$$
综上，可得支持向量机数学模型：
$$\begin{array}{rl}\underset{\mathbf{w},b}{\min }& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }& y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,m.\end{array}\text{\hspace{1em}(3a)(3b)}$$
目标函数表示：过「支持向量」的平行于「最优划分超平面」的两个超平面距离最大（间隔最大）。

目标函数中乘 $1/2$ 的目的是便于求导。

思考

• 约束方程为什么乘 $y_i$？

  ${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b$ 的符号与类别标记 $y_i$ 的符号是否一致能够表示分类是否正确。

• 约束方程右端为什么是1？可以为其他数吗？

  约束方程右端的数可以改成任意的正数。若改为正数 $a$ ，意味着所有向量距离最优划分超平面最小距离为 $a$，参数 $\mathbf{w}、b$ 的值与原来的为 1 时的只差 $a$ 倍。

• 为什么取 $y_i$ 为 -1 或 1？

  两个值表示两类不同样本，和 ${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b=\pm 1$ 式中的 $1$ 没有关系，也可取其他值，如：0 和 1、1 和 2，……此处定为 -1 或 1 是为了便于推导数学模型，如公式 (2) 的简洁形式。

• 为什么设支持向量所在超平面方程为 ${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b=\pm 1$？可以是 ${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b=\pm 5$ 吗?

  原则上说，这两条直线可以是 ${\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b=\pm k$ ，其中，$k$ 为任意常数。若对上式两边同时乘以 $\frac{1}{k}$，并令 ${\mathbf{w}}^{\mathbf{T}}=\frac{1}{k}{\mathbf{w}}^{\mathbf{T}},b=\frac{1}{k}b$ ，直线改为： ${\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b=\pm 1$，最优划分超平面依然是 ${\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b=0$ ，但是数学模型的最优值发生变化。

求解

公式 (3) 为凸二次规划（convex quadratic programming）问题，处理用优化计算包求解，还可利用原问题的对偶问题来求解。

---

参考：

《机器学习》周志华

《统计学习方法（第二版）》李航

支持向量机（SVM） | notebook (yubincloud.github.io)

支持向量机算法（SVM）详细讲解_qq_38422157的博客-CSDN博客_

浙江大学胡浩基机器学习课程现场录播合集 p=7

【吃瓜教程】《机器学习公式详解》（南瓜书） p=8