项目运行
环境配置:
Jdk1.8 + Tomcat7.0 + Mysql + HBuilderX(Webstorm也行)+ Eclispe(IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持)。
项目技术:
SSM + mybatis + Maven + Vue 等等组成,B/S模式 + Maven管理等等。
环境需要
1.运行环境:最好是java jdk 1.8,我们在这个平台上运行的。其他版本理论上也可以。
2.IDE环境:IDEA,Eclipse,Myeclipse都可以。推荐IDEA;
3.tomcat环境:Tomcat 7.x,8.x,9.x版本均可
4.硬件环境:windows 7/8/10 1G内存以上;或者 Mac OS;
5.是否Maven项目: 否;查看源码目录中是否包含pom.xml;若包含,则为maven项目,否则为非maven项目
6.数据库:MySql 5.7/8.0等版本均可;
毕设帮助,指导,本源码分享,调试部署(见文末)
3.3网站功能分析
考虑到实际生活中在政府公用车辆管理方面的需要以及对该系统认真的分析,将系统权限按管理员和用户这两类涉及用户划分。
(a) 管理员;管理员使用本系统涉到的功能主要有:个人中心、用户管理、车辆类型管理、排班信息管理、车辆信息管理、车辆申请管理、派遣登记管理、车辆归队管理、车辆台账管理、管理员管理、交流论坛、系统管理等功能。管理员用例图如图3-1所示。
 图3-1 管理员用例图
图3-1 管理员用例图
(b)用户进入系统前台可以实现首页、车辆信息、交流论坛、公告资讯、个人中心、后台管理、在线咨询等功能。用户用例图如图3-2所示。

图3-2用户用例图
3.4系统流程的分析
由于不同的系统实际使用用户角色的不同,他们的业务分析也会变得有所不一样,为了论述方便接下来都将以管理员用户功能权限下的系统业务流程来分析,如下图所展示:
3.4.1 用户管理的流程
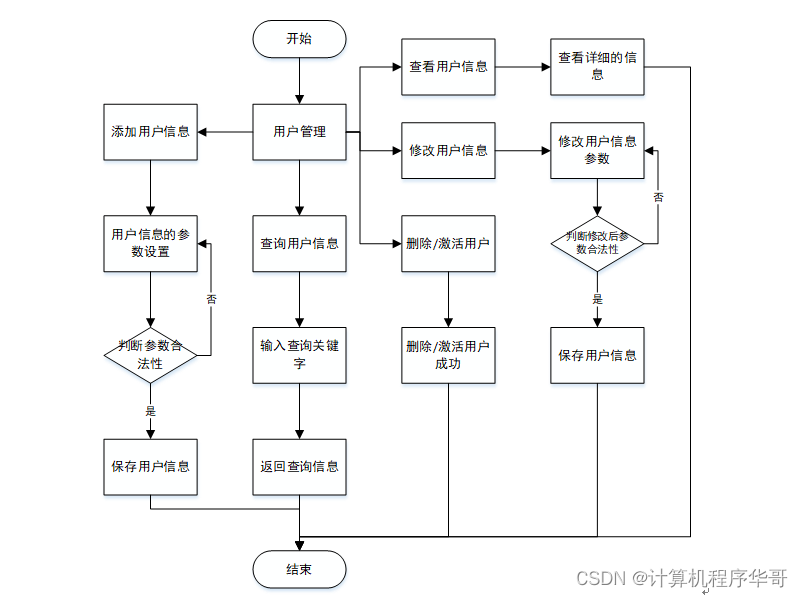
图3-3 用户管理流程
3.4.2个人中心管理流程
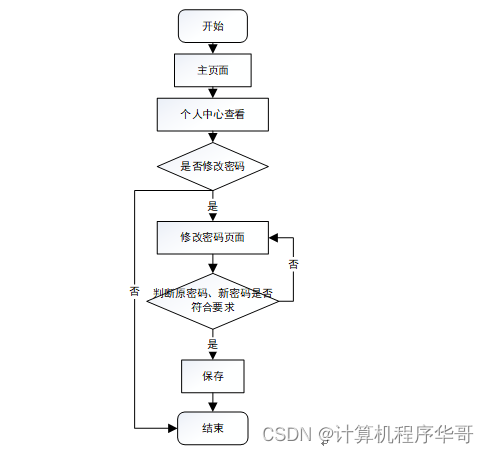
图3-4 个人中心管理流程
3.4.3登录流程
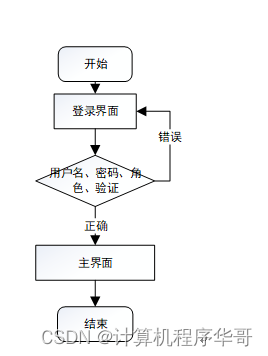
图3-5 登录流程
4.1 软件功能模块设计
网站整功能如下图所示:

图 4-1 政府公用车辆管理系统总体功能模块图
4.2数据库设计
4.2.1概念模型设计
概念模型是对现实中的问题出现的事物的进行描述,ER图是由实体及其关系构成的图,通过E-R图可以清楚地描述系统涉及到的实体之间的相互关系。
用户注册实体图如图4-2所示:

图4-2用户注册实体图
车辆信息实体图如图4-3所示:
 图4-3车辆信息实体图
图4-3车辆信息实体图
排班信息实体图如图4-4所示:

图4-4排班信息实体图
车辆归队实体图如图4-5所示:
 图4-5车辆归队实体图
图4-5车辆归队实体图
5.1系统功能模块
政府公用车辆管理系统,在网站首页可以查看首页、车辆信息、交流论坛、公告资讯、个人中心、后台管理、在线咨询等内容,如图5-1所示。
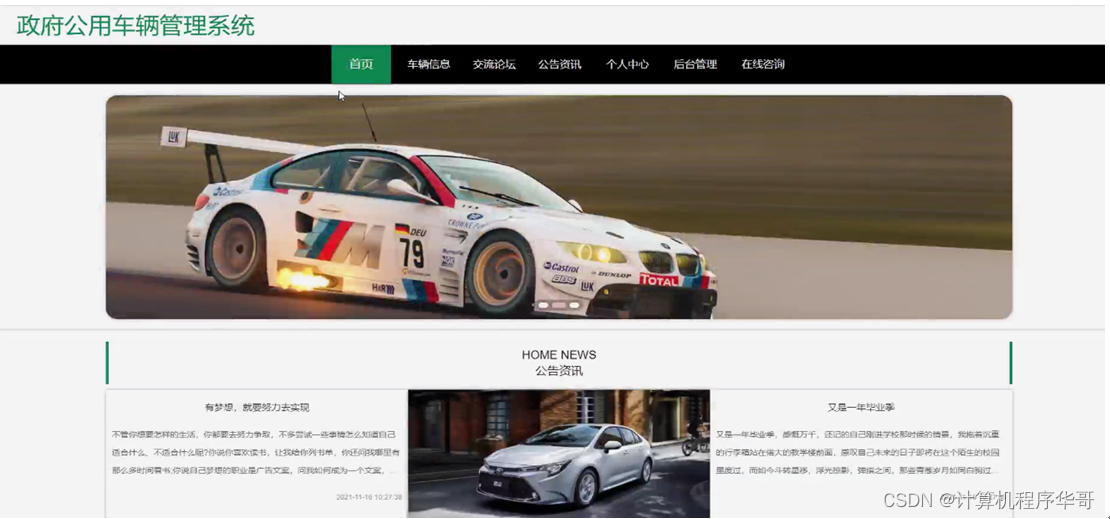
图5-1网站首页界面图
用户注册,在用户注册页面通过填写用户名、密码、姓名、身份证、手机等信息完成用户注册操作,如图5-2所示。

图5-2用户注册界面图
车辆信息,在车辆信息页面可以查看车辆编号、车辆名称、车辆类型、图片、车辆颜色、车牌号、停放位置、车辆详情、车辆状况等内容,点击申请,填写车辆编号、车辆名称、车牌号、车辆类型、车辆颜色、申请理由、申请天数、申请时间、用户名、姓名、手机等信息进行车辆申请;如图5-3所示。
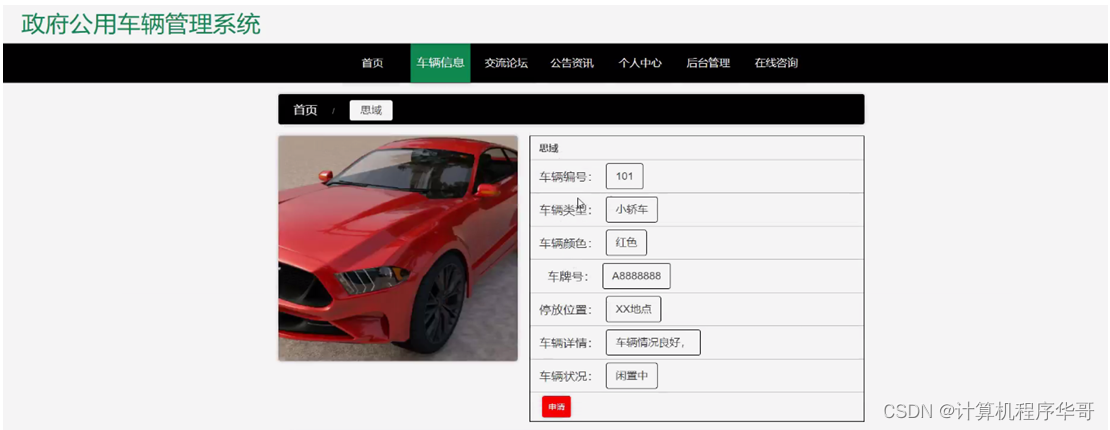

图5-3车辆信息界面图
交流论坛,在交流论坛页面可以查看其他用户发布的论坛,也能通过输入标题、类型、内容来发布新帖子;如图5-4所示。

图5-4交流论坛界面图
个人中心,在个人信息页面通过填写用户名、密码、姓名、性别、上传图片、身份证、手机等信息进行更新信息,还可以根据需要对我的发布、我的收藏进行相对应操作,如图5-5所示。

图5-5个人中心界面图
在线咨询,在在线咨询页面可以发布想要咨询的内容给管理员进行咨询,管理员在后台可以查看并回复,如图5-6所示。

图5-6在线咨询界面图
5.2管理员功能模块
管理员进行登录,进入系统前在登录页面根据要求填写用户名和密码,选择角色等信息,点击登录进行登录操作,如图5-7所示。

图5-7管理员登录界面图
管理员登录系统后,可以对个人中心、用户管理、车辆类型管理、排班信息管理、车辆信息管理、车辆申请管理、派遣登记管理、车辆归队管理、车辆台账管理、管理员管理、交流论坛、系统管理等进行相应的操作管理,如图5-8所示。

图5-8管理员功能界面图
用户管理,在用户管理页面,可以对用户名、姓名、性别、头像、身份证、手机等内容进行排班、查看、修改、删除或批量删除等操作,点击排班,通过填写编号、名称、排班日期、排班时间、用户名、姓名、手机、排班内容等信息进行排班,如图5-9所示。

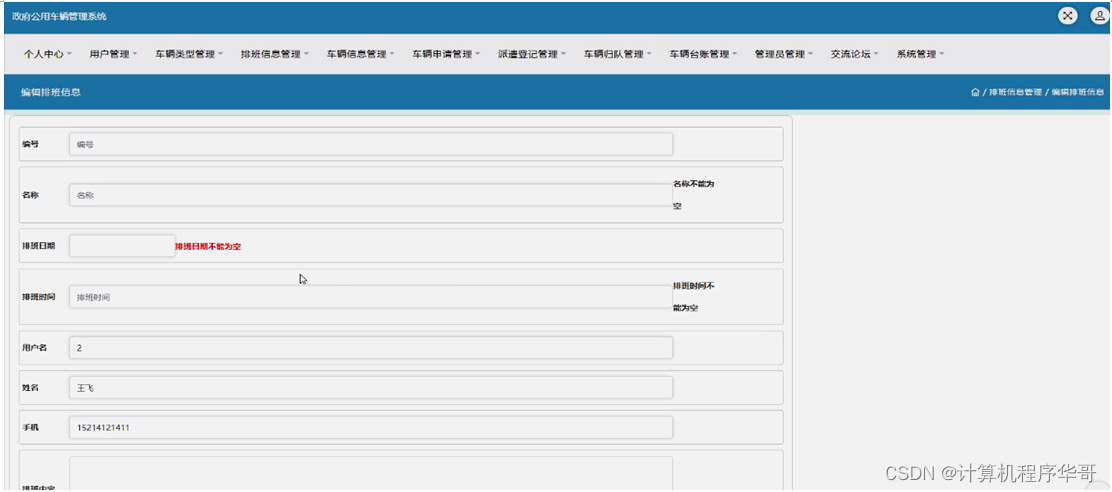
图5-9用户管理界面图
车辆类型管理,在车辆类型管理页面可以对车辆类型进行修改或删除、添加、批量删除等操作,如图5-10所示。

图5-10车辆类型管理界面图
排班信息管理,在排班信息管理页面可以对编号、名称、排班日期、排班时间、用户名、姓名、手机、排班内容等进行查看、修改或删除、批量删除等操作,如图5-11所示。
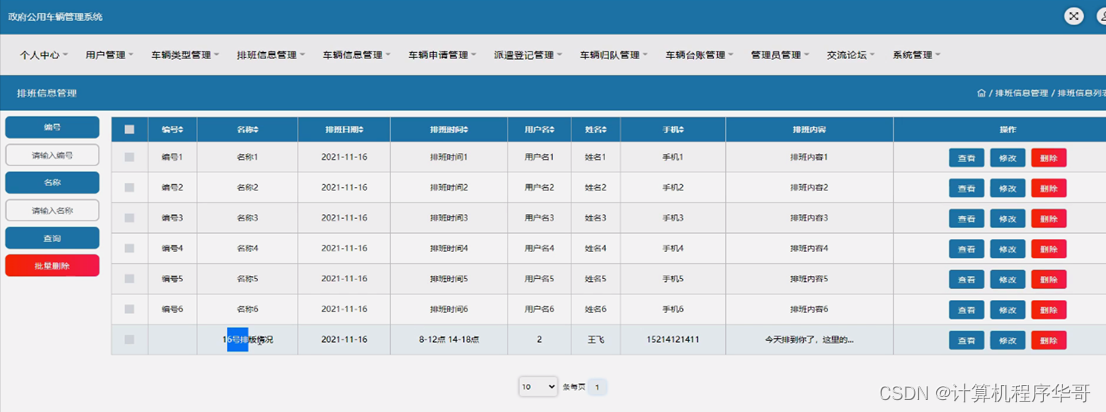
图5-11排班信息管理界面图
车辆信息管理,在车辆信息管理页面可以对车辆编号、车辆名称、车辆类型、图片、车辆颜色、车牌号、停放位置、车辆详情、车辆状况等内容进行查看、修改、删除或添加、批量删除等操作,如图5-12所示。
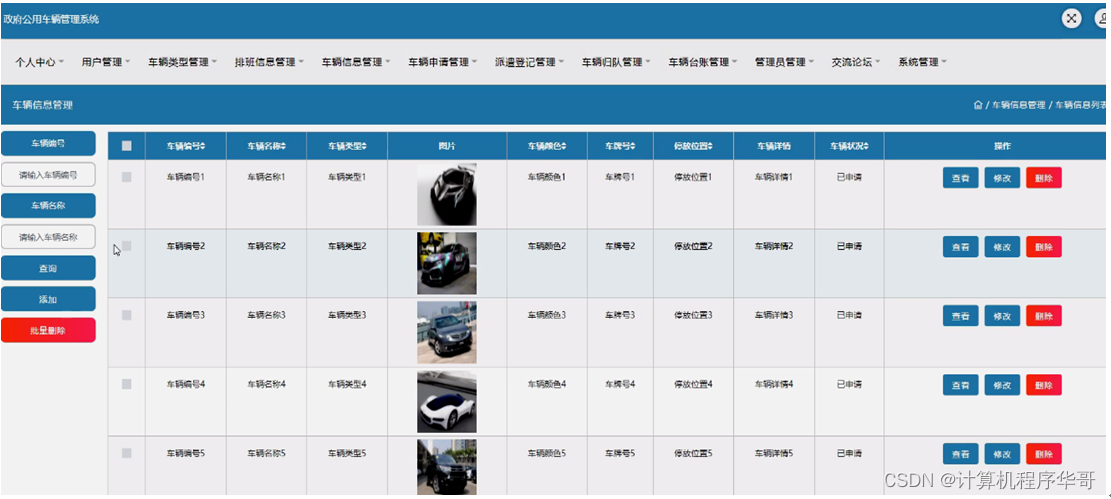
图5-12车辆信息管理界面图
车辆申请管理,在车辆申请管理页面可以对车辆编号、车辆名称、车牌号、车辆类型、车辆颜色、申请理由、申请天数、申请时间、用户名、姓名、手机、是否审核、审核回复等内容进行审核、派遣、查看、修改、删除或批量删除、查看统计图等操作,如图5-13所示。

图5-13车辆申请管理界面图
车辆派遣管理,在车辆派遣管理页面,可以对车牌编号、车辆名称、车辆车辆、车牌号、用户名、姓名、手机、车辆颜色、出车日期、登记内容等进行修改、删除、查看或批量删除等操作,如图5-14所示。

图5-14车辆派遣管理界面图


![[MQ] MQ的应用场景及Docker安装RabbitMQ](https://img-blog.csdnimg.cn/d71f0b3d20204d1eaa8056536ee544ac.png)
![PGL图学习之图神经网络GraphSAGE、GIN图采样算法[系列七]](https://img-blog.csdnimg.cn/img_convert/88a1ef82ca61113ad7be6ab3cfc05665.jpeg)





![[相向双指针] 167. 两数之和 II - 输入有序数组,15. 三数之和,11. 盛最多水的容器,42. 接雨水](https://img-blog.csdnimg.cn/cbafacb01a7f474e96f32ef83735f770.png)