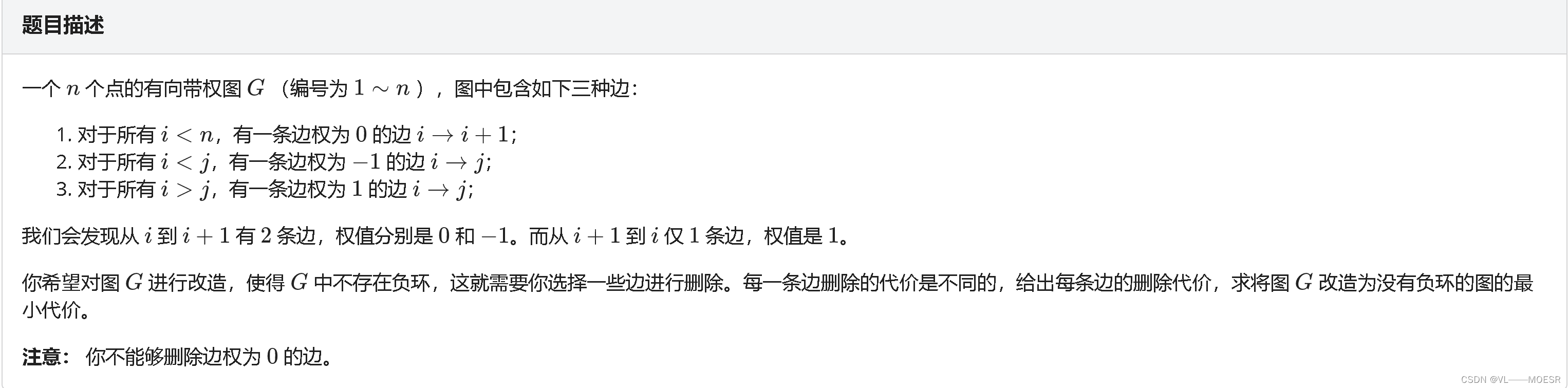
思路：

dis i 代表1 到 i 的最短路
因为它要求没有负环
无负环和可以求出最短路是充要条件
然后dis i 和 dis (i+1)相差最多不超过1
因为有0边的存在
然后就对边的大小进行分类讨论
如果i<j即e i,j 为-1
那么dis (i) - 1 >= dis j
然后移项
dis i - dis j >= 1
这个式子代表的意思就是i到j这之间所有的边都要删掉
然后如果i>j即e i,j 是1
那么dis (i) + 1 >= dis j
移项
dis j - dis i <= 1
这意味着从[i,n]到[1,j]的所有边都要删掉
我们设fi = disi - dis（i+1）,然后这绝对是一个非负数。。而且值只能是0或1，因为根据上面那个dis j - dis i <= 1，用fi表示就是fj + f(j+1)+……+f(i-1)<=1，所以我们就可以考虑构造fi
因为fj + f(j+1)+……+f(i-1)<=1，所以我们想到设dp[i][j]表示最后的两个1在i和j这里的最小删边代价
然后转移就是dp[i][j]=min(d[i][j],dp[j][k]+{从[i,n]到[1,j)的边的价值和} + {从[j,i) 到 [j,i) 的边的价值和})
然后中间那个价值和在循环里用前缀和求

$code$

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long

using namespace std;

const ll MAXN = 505;

ll n;
ll a[MAXN][MAXN], sum[MAXN][MAXN], sum2[MAXN][MAXN], dp[MAXN][MAXN];

int main() {
	scanf("%lld", &n);
	for(ll i = 1; i <= n; i ++) {
		for(ll j = 1; j <= n; j ++) {
			if(i == j) continue;
			scanf("%lld", &a[i][j]);
		}
	}
	n ++;
	memset(dp, 0x7f, sizeof(dp));
	dp[0][0] = 0;
	for(ll i = 1; i < n; i ++) {
		for(ll j = 0; j < i; j ++) {
			for(ll k = i + 1; k <= n; k ++)
				sum[i][j] += a[k][j];
			if(j) sum[i][j] += sum[i][j - 1];
		}
		for(ll j = i - 1; j >= 0; j --) {
			for(ll k = j + 1; k <= i; k ++)
				sum2[i][j] += a[j + 1][k];
			if(j + 1 < i - 1) sum2[i][j] += sum2[i][j + 1];
		}
		for(ll j = 0; j < i; j ++) {
			for(ll k = 0; k <= j; k ++)
				dp[i][j] = min(dp[i][j], dp[j][k] + sum[i][j] - sum[i][k] + sum2[i][j]);
		} 
	}
	ll ans = 1e18;
	for(ll i = 0; i < n; i ++)
		ans = min(ans, dp[n - 1][i]);
	printf("%lld", ans);
	return 0;
}