关联式容器

set

set的模板参数列表

set的构造

set的使用

multiset

map

map的模板参数

map的构造

map的容量与元素访问

map的使用

multimap

底层结构

AVL树

节点的定义

实现

图解

红黑树

性质

节点的定义

实现

图解

红黑树模拟实现STL中的map和set

MyMap.h

MySet.h

RBTree.h

关联式容器

序列式容器:底层为线性序列的数据结构，里面存储的是元素本身

关联式容器:里面存储的是<key, value>结构的键值对，在数据检索时比序列式容器效率更高

(键值对:用来表示具有一一对应关系的一种结构，该结构中一般只包含两个成员变量key和value，key代表键值，value表示与key对应的信息)

树型结构的关联式容器主要有map、set、multimap、multiset。这四种容器的共同点是：使用红黑树作为底层结果，容器中的元素是一个有序的序列

set

set的模板参数列表

template < class T,             // set::key_type/value_type           
class Compare = less<T>,        // set::key_compare/value_compare          
class Alloc = allocator<T>      // set::allocator_type          
> class set;

T: set中存放元素的类型

Compare：set中元素默认按照小于来比较

Alloc：set中元素空间的管理方式，使用STL提供的空间配置器管理

set的构造

函数声明	功能介绍
set (const Compare& comp = Compare(), const Allocator& = Allocator() );	构造空的set
set (InputIterator first, InputIterator last, const Compare& comp = Compare(), const Allocator& = Allocator() );	用[first, last)区间中的元素构造set
set ( const set<Key,Compare,Allocator>& x);	拷贝构造

set的使用

pair<iterator,bool> insert (const value_type& x )	在set中插入元素x，实际插入的是<x, x>构成的键值对，如果插入成功，返回<该元素在set中的位置，true>,如果插入失败，说明x在set中已经存在，返回<x在set中的位置，false>
void erase ( iterator position )	删除set中position位置上的元素
size_type erase ( const key_type& x )	删除set中值为x的元素，返回删除的元素的个数
void erase ( iterator first, iterator last )	删除set中[first, last)区间中的元素
void swap (set<Key,Compare,Allocator>& st );	交换set中的元素
void clear ( )	将set中的元素清空
iterator find ( const key_type& x ) const	set中值为x的元素的位置
size_type count ( const key_type& x ) const	set中值为x的元素的个数

void test_set1()
{
	//排序+去重
	set<int> s;
	s.insert(3);
	s.insert(8);
	s.insert(7);
	s.insert(6);
	s.insert(2);
	s.insert(3);
	s.insert(6);

	set<int>::iterator it = s.begin();

	while (it != s.end())
	{
		cout << *it << " ";
		++it;
	}
	cout << endl;

	set<int>::iterator pos = s.find(30);
	if (pos != s.end())
	{
		//pos必须是一个有效的迭代器
		s.erase(pos);
	}

	cout << s.erase(30) << endl;
	cout << s.erase(3) << endl;

	for (auto e : s)
	{
		cout << e << " ";
	}
	cout << endl;
}

multiset

multiset是按照特定顺序存储元素的容器，其中元素可以重复

void test_multiset()
{
	//排序
	multiset<int> s;
	s.insert(3);
	s.insert(1);
	s.insert(5);
	s.insert(2);
	s.insert(8);
	s.insert(1);
	s.insert(8);
	s.insert(1);

	auto it = s.begin();
	while (it != s.end())
	{
		cout << *it << " ";
		++it;
	}
	cout << endl;

	//find 的val有多个值时，返回中序第一个val值所在节点的迭代器
	multiset<int>::iterator pos = s.find(8);
	while (pos != s.end())
	{
		cout << *pos << " ";
		++pos;
	}
	cout << endl;

	/*pos = s.find(1);
	while (pos != s.end() && *pos == 1)
	{
		auto next = pos;
		++next;

		s.erase(pos);

		pos = next;
	}*/

	cout << s.erase(1) << endl;     //返回删了几个

	for (auto e : s)
	{
		cout << e << " ";
	}
	cout << endl;

	pos = s.find(5);
	if (pos != s.end())
	{
		//不允许修改
		//*pos += 10;
	}
}

map

map的模板参数

template < class Key,                          // map::key_type         
class T,                                       // map::mapped_type           
class Compare = less<Key>,                     // map::key_compare           
class Alloc = allocator<pair<const Key,T> >    // map::allocator_type           
> class map;

key: 键值对中key的类型

T：键值对中value的类型

Compare: 比较器的类型，map中的元素是按照key来比较的，缺省情况下按照小于来比较，一般情况下(内置类型元素)该参数不需要传递，如果无法比较时(自定义类型)，需要用户自己显式传递比较规则(一般情况下按照函数指针或者仿函数来传递)

Alloc：通过空间配置器来申请底层空间，不需要用户传递，除非用户不想使用标准库提供的空间配置器

map的构造

map()

构造一个空的map

map的容量与元素访问

bool empty ( ) const	检测map中的元素是否为空
size_type size() const	map中有效元素的个数
mapped_type& operator[] (const key_type& k)	返回key对应的value的引用

map的使用

pair<iterator,bool> insert (const value_type& x)	插入(pair<K,V>)键值对x,返回值也是键值对：iterator代表新插入元素的位置，bool代表是否插入成功
void erase ( iterator position )	删除position位置上的元素
size_type erase ( const key_type& x )	删除键值为x的元素
void erase ( iterator first, iterator last )	删除[first, last)区间中的元素
void swap (map<Key,T,Compare,Allocator>& mp )	交换两个map中的元素
void clear ( )	将map中的元素清空
iterator find ( const key_type& x )	如果找到，返回该元素的位置的迭代器，否则返回end
const_iterator find ( const key_type& x ) const	找到返回该元素的位置的const迭代器，否则返回cend
size_type count ( const key_type& x ) const	返回key为x的键值在map中的个数，map中key是唯一的，因此该函数的返回值要么为0，要么为1，因此也可以用该函数来检测一个key是否在map中

void test_map1()
{
	map<string, string> dict;
	pair<string, string> kv1("sort", "排序");
	dict.insert(kv1);
	dict.insert(pair<string, string>("string", "字符串"));
	//自动推导类型
	dict.insert(make_pair("test", "测试"));

	map<string, string>::iterator it = dict.begin();
	while (it != dict.end())
	{
		//cout << (*it).first << ":" << (*it).second << endl;
		cout << it->first << ":" << it->second << endl;
		++it;
	}
	cout << endl;

	for (auto& kv : dict)
	{
		cout << kv.first << ":" << kv.second << endl;
	}
	cout << endl;
}

void test_map2()
{
	string arr[] = { "苹果", "苹果", "香蕉", "苹果", "香蕉", "苹果", "樱桃" };
	map<string, int> countMap;
	//for (auto& str : arr)
	//{
	//	auto ret = countMap.find(str);
	//	if (ret == countMap.end())
	//	{
	//		countMap.insert(make_pair(str, 1));
	//	}
	//	else
	//	{
	//		ret->second++;
	//	}
	//}

	/*for (auto& str : arr)
	{
		auto kv = countMap.insert(make_pair(str, 1));
		if (kv.second == false)
		{
			kv.first->second++; 
		}
	}*/
 
	for (auto& str : arr)
	{
		countMap[str]++;
	}

	for (auto& kv : countMap)
	{
		cout << kv.first << ":" << kv.second << endl;
	}
	cout << endl;
}

void test_map3()
{
	map<string, string> dict;
	dict.insert(make_pair("sort", "排序"));
	dict.insert(make_pair("left", "左边"));
	dict.insert(make_pair("left", "剩余"));

	dict["left"] = "剩余";   //修改
	dict["test"];            //插入
	cout << dict["sort"] << endl;  //查找

	dict["string"] = "字符串";  //插入+修改
}

void test_map4()
{
	multimap<string, string> dict;
	dict.insert(make_pair("sort", "排序"));
	dict.insert(make_pair("left", "左边"));
	dict.insert(make_pair("left", "剩余"));
	dict.insert(make_pair("left", "剩余"));

	cout << dict.count("left") << endl;
}

multimap

multimap中的key是可以重复的

TopK问题

struct CountVal
{
	bool operator()(const pair<string, int>& l, const pair<string, int>& r)
	{
		//return l.second > r.second;
		return l.second < r.second;
	}
};

struct CountIterVal
{
	bool operator()(const map<string, int>::iterator& l, const map<string, int>::iterator& r)
	{
		//return l->second > r->second;
		return l->second < r->second;
	}
};

//topK
void GetFavoriteFruit(const vector<string>& fruits, size_t k)
{
	map<string, int> countMap;
	for (auto& str : fruits)
	{
		countMap[str]++;
	}

	//数据量不大，排序
	//sort
	//multimap
	/*vector<pair<string, int>> sortV;
	for (auto& kv : countMap)
	{
		sortV.push_back(kv);
	}
	sort(sortV.begin(), sortV.end(), CountVal());

	for (int i = 0; i < k; ++i)
	{
		cout << sortV[i].first << ":" << sortV[i].second << endl;
	}
	cout << endl;*/

	/*vector<map<string, int>::iterator> sortV;
	auto it = countMap.begin();
	while (it != countMap.end())
	{
		sortV.push_back(it);
		++it;
	}

	sort(sortV.begin(), sortV.end(), CountIterVal());

	for (int i = 0; i < k; ++i)
	{
		cout << sortV[i]->first << ":" << sortV[i]->second << endl;
	}
	cout << endl;*/

	//multimap<int, string, greater<int>> sortMap;
	//for (auto& kv : countMap)
	//{
	//	sortMap.insert(make_pair(kv.second, kv.first));
	//}

	堆
	//priority_queue<pair<string, int>, vector<pair<string, int>>, CountVal> pq;
	//for (auto& kv : countMap)
	//{
	//	pq.push(kv);
	//}
	//while (k--)
	//{
	//	cout << pq.top().first << ":" << pq.top().second << endl;
	//	pq.pop();
	//}
	//cout << endl;

	priority_queue<map<string, int>::iterator, vector<map<string, int>::iterator>, CountIterVal> pq;
	auto it = countMap.begin();
	while (it != countMap.end())
	{
		pq.push(it);
		++it;
	}

	while (k--)
	{
		cout << pq.top()->first << ":" << pq.top()->second << endl;
		pq.pop();
	}
	cout << endl;
}


int main()
{
	//test_set1();
	//test_multiset();
	//test_map1();
	//test_map4();

	vector<string> v = { "苹果", "苹果", "香蕉", "苹果", "香蕉", "苹果", "樱桃", "哈密瓜", "榴莲", "榴莲", "苹果" };
	GetFavoriteFruit(v, 3);

	return 0;
}

底层结构

AVL树

AVL树是空树或者是具有以下性质的二叉搜索树：

它的左右子树都是AVL树

左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

节点的定义

template<class K, class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	pair<K, V> _kv;

	int _bf;

	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
		, _kv(kv)
	{}
};

实现

template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;

public:
	AVLTree()
		:_root(nullptr)
	{}

	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;

		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}

		//控制平衡
		while (parent)
		{
			if (cur == parent->_left)
				parent->_bf--;
			else
				parent->_bf++;

			if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				if (parent->_bf == -2 && cur->_bf == -1)
					RotateR(parent);
				else if (parent->_bf == 2 && cur->_bf == 1)
					RotateL(parent);
				else if (parent->_bf == -2 && cur->_bf == 1)
					RotateLR(parent);
				else if (parent->_bf == 2 && cur->_bf == -1)
					RotateRL(parent);
				else
				{
					assert(false);
				}

				break;
			}
			else
			{
				assert(false);
			}
		}

		return true;
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		Node* parentParent = parent->_parent;

		parent->_parent = subR;
		subR->_left = parent;

		if (parent == _root)
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
				parentParent->_left = subR;
			else
				parentParent->_right = subR;

			subR->_parent = parentParent;
		}

		subR->_bf = parent->_bf = 0;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		Node* parentParent = parent->_parent;

		parent->_parent = subL;
		subL->_right = parent;

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = subL;
				subL->_parent = parentParent;
			}
			else
			{
				parentParent->_right = subL;
				subL->_parent = parentParent;
			}
		}

		subL->_bf = parent->_bf = 0;
	}

	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else
		{
			assert(false);
		}

	}


	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
			subRL->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	void InOrder()
	{
		_InOrder(_root);
	}

	void _InOrder(Node* root)
	{
		if (root == NULL)
			return;

		_InOrder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_InOrder(root->_right);
	}

	bool IsBalance()
	{
		return _IsBalance(_root);
	}

	int Height(Node* root)
	{
		if (root == NULL)
			return 0;
		int leftHeight = Height(root->_left);
		int rightHeight = Height(root->_right);
		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}

	bool _IsBalance(Node* root)
	{
		if (root == NULL)
			return true;

		// 对当前树进行检查
		int leftHeight = Height(root->_left);
		int rightHeight = Height(root->_right);

		if (rightHeight - leftHeight != root->_bf)
		{
			cout << root->_kv.first << "现在是:" << root->_bf << endl;
			cout << root->_kv.first << "应该是:" << rightHeight - leftHeight << endl;
			return false;
		}

		return abs(rightHeight - leftHeight) < 2
			&& _IsBalance(root->_left)
			&& _IsBalance(root->_right);
	}
private:
	Node* _root;
};

图解

右单旋

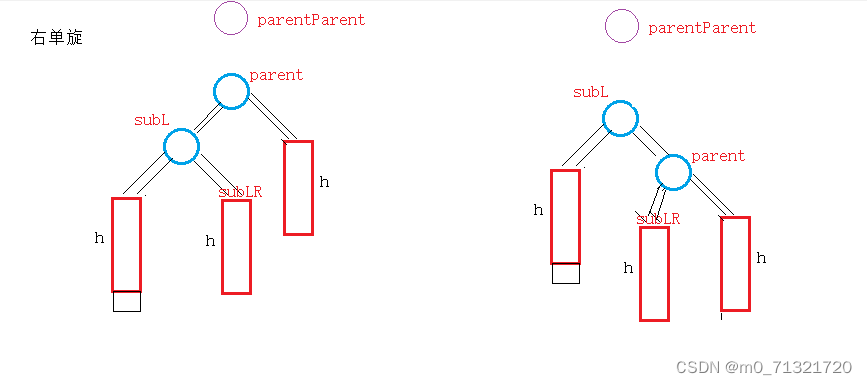
左单旋

右左双旋

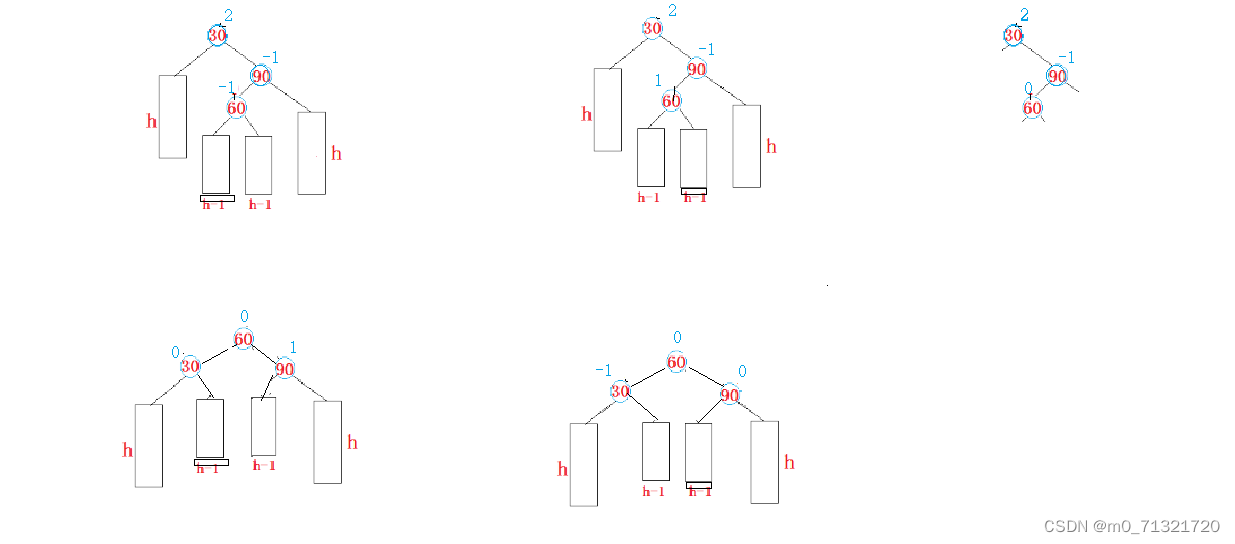
左右双旋(同理)

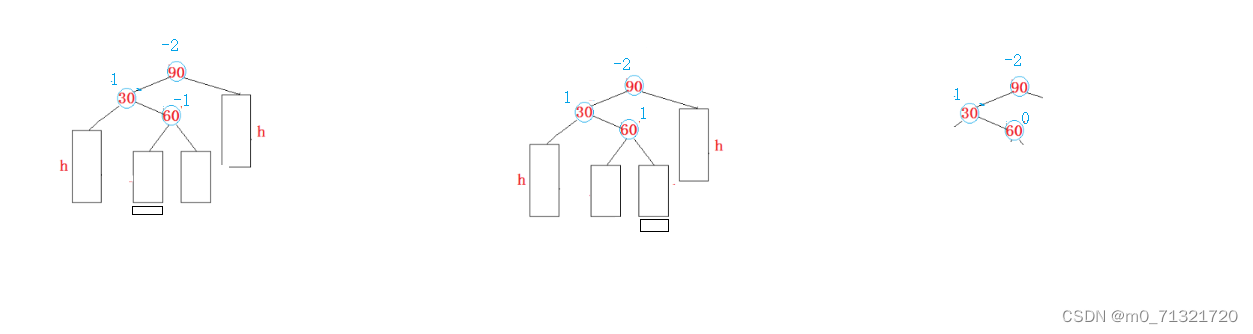
红黑树

性质

1. 每个结点不是红色就是黑色

2. 根节点是黑色

3. 如果一个节点是红色，则它的两个孩子结点是黑色(没有连续的红节点)

4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点

(每条路径黑色节点数量相同)

5. 每个叶子结点都是黑色(空结点)

节点的定义

enum Colour
{
	RED,
	BLACK
};

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	pair<K, V> _kv;

	Colour _col;

	RBTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(RED)
		, _kv(kv)
	{}
};

实现

template<class K, class V>
struct RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	RBTree()
		:_root(nullptr)
	{}

	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(kv);
		cur->_col = RED;         //新增节点
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}

		//控制平衡
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				//1.uncle存在且为红
				if (uncle && uncle->_col == RED)
				{
					//变色，继续向上处理
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
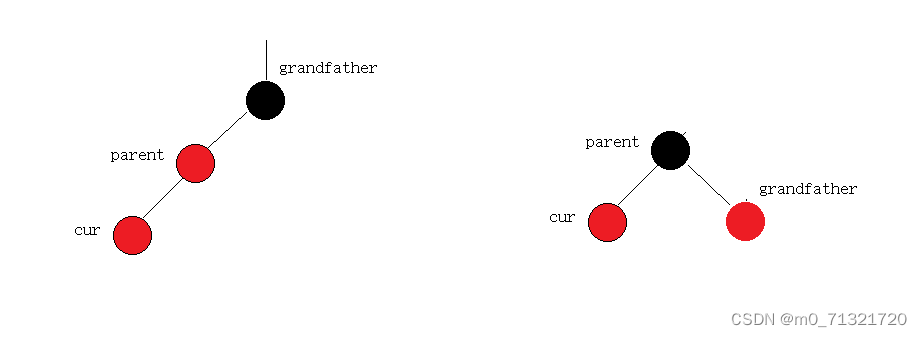
				else	// uncle不存在    存在且为黑					
					//        g
					//     p
					//  c

					//        g
					//     p
					//        c

				{
					if (cur == parent->_left)
					{
						//单旋
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
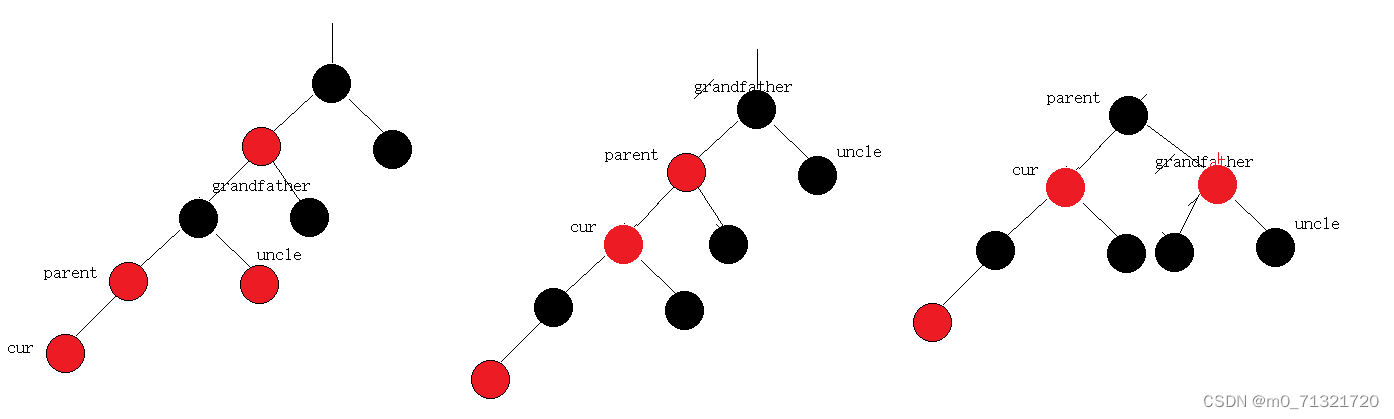
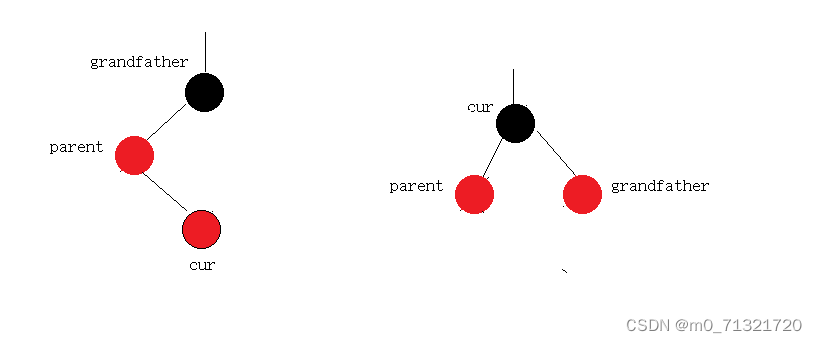
					else
					{
						//双旋
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
			else     //parent == grandfather->_right
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					//变色  继续向上调整
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else     //  uncle不存在   存在且为黑
				{
					//  g    
					//     p
					//        c

					//  g
					//     p
					//  c
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

		_root->_col = BLACK;
		return true;
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		Node* parentParent = parent->_parent;
		subR->_left = parent;
		parent->_parent = subR;

		if (_root == parent)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
				parentParent->_left = subR;
			else
				parentParent->_right = subR;
			subR->_parent = parentParent;
		}
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		Node* parentParent = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
				parentParent->_left = subL;
			else
				parentParent->_right = subL;

			subL->_parent = parentParent;
		}
	}

	void InOrder()
	{
		_InOrder(_root);
	}

	void _InOrder(Node* root)
	{
		if (root == NULL)
			return;

		_InOrder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_InOrder(root->_right);
	}

	bool IsBalance()
	{
		if (_root && _root->_col == RED)
		{
			cout << "根节点不是黑色" << endl;
			return false;
		}

		// 最左路径黑色节点数量做基准值
		int banchmark = 0;
		Node* left = _root;
		while (left)
		{
			if (left->_col == BLACK)
				++banchmark;

			left = left->_left;
		}

		int blackNum = 0;
		return _IsBalance(_root, banchmark, blackNum);
	}

	bool _IsBalance(Node* root, int banchmark, int blackNum)
	{
		if (root == nullptr)
		{
			if (banchmark != blackNum)
			{
				cout << "存在路径黑色节点的数量不相等" << endl;
				return false;
			}

			return true;
		}

		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << "出现连续红色节点" << endl;
			return false;
		}

		if (root->_col == BLACK)
		{
			++blackNum;
		}

		return _IsBalance(root->_left, banchmark, blackNum)
			&& _IsBalance(root->_right, banchmark, blackNum);
	}

	int Height()
	{
		return _Height(_root);
	}

	int _Height(Node* root)
	{
		if (root == NULL)
			return 0;
		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}

private:
	Node* _root;
};

void TestRBTree()
{
	RBTree<int, int> t;
	vector<int> v;
	srand(time(0));
	int N = 1000;
	for (int i = 0; i < N; ++i)
	{
		//v.push_back(rand());
		v.push_back(i);
	}
	//int a[] = {5,4,3,2,1,0};
	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	for (auto e : v)
	{
		t.Insert(make_pair(e, e));
		if (!t.IsBalance())
		{
		cout << "Insert" << e << endl;
		}
	}
	t.InOrder();
	cout << t.IsBalance() << endl;
	cout << "高度:" << t.Height() << endl;
}

图解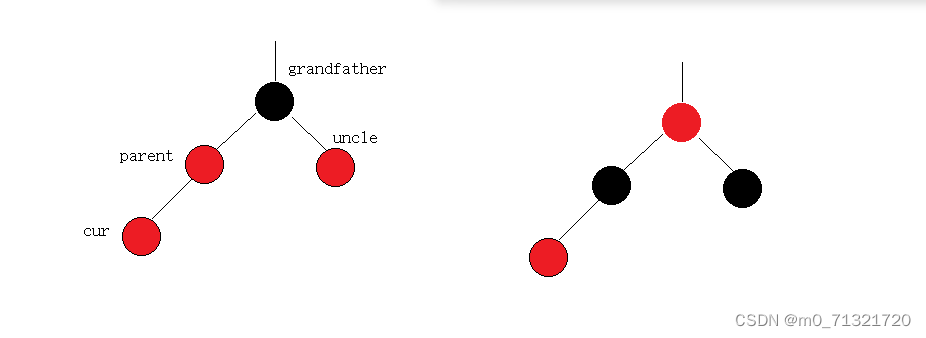

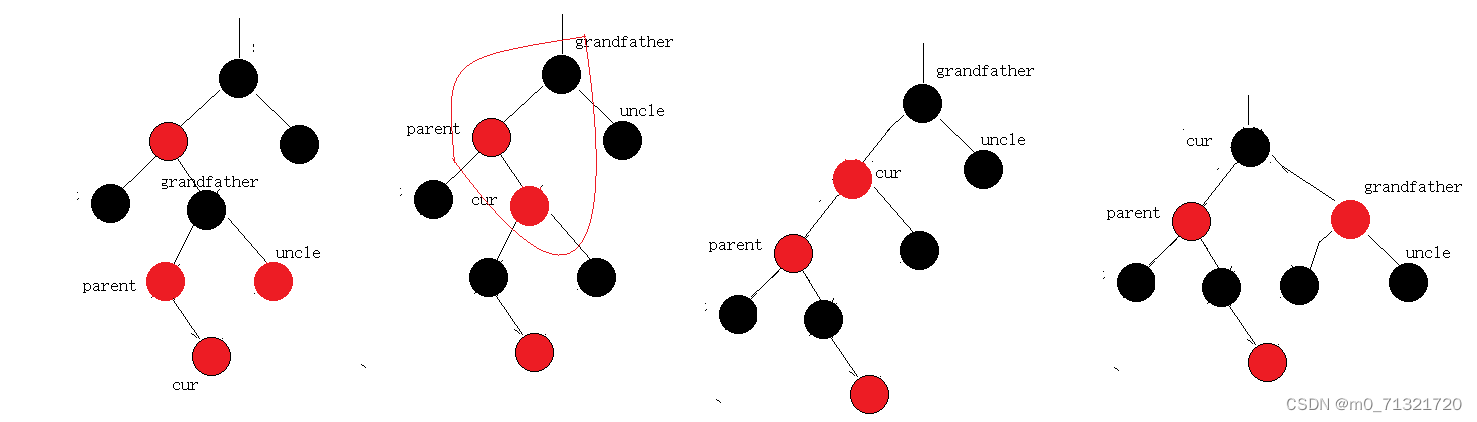
红黑树模拟实现STL中的map和set

MyMap.h

namespace qwe
{
	template<class K, class V>
	class map
	{
	public:
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};

		typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const pair<K, V>& kv)
		{
			return _t.Insert(kv);
		}

		iterator find(const K& key)
		{
			return _t.Find(key);
		}

		V& operator[](const K& key)
		{
			auto ret = _t.Insert(make_pair(key, V()));
			return ret.first->second;
		}

	private:
		RBTree<K, pair<K, V>, MapKeyOfT> _t;
	};

	void test_map()
	{
		map<string, string> dict;
		dict.insert(make_pair("sort", "排序"));
		dict.insert(make_pair("string", "字符串"));
		dict.insert(make_pair("map", "地图"));
		dict["left"];
		dict["left"] = "左边";
		dict["map"] = "地图,映射";

		auto it = dict.begin();
		while (it != dict.end())
		{
			cout << it->first << ":" << it->second << endl;
			++it;
		}
		cout << endl;
	}
}

MySet.h

namespace qwe
{
	template<class K>
	class set
	{
	public:
		struct SetKeyOfT
		{
			const K& operator()(const K& k)
			{
				return k;
			}
		};
		typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		pair <iterator, bool> insert(const K& key)
		{
			return _t.Insert(key);
		}

		iterator find(const K& key)
		{
			return _t.Find();
		}
	private:
		RBTree<K, K, SetKeyOfT> _t;
	};
}

RBTree.h

enum Colour
{
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	T _data;

	Colour _col;

	RBTreeNode(const T& data)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(RED)
		, _data(data)
	{}
};

template<class T, class Ref, class Ptr>
struct RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T, Ref, Ptr> Self;
	Node* _node;

	RBTreeIterator(Node* node)
		:_node(node)
	{}

	Ref operator*()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &_node->_data;
	}

	Self& operator++()
	{
		if (_node->_right)
		{
			Node* min = _node->_right;
			while (min->_left)
			{
				min = min->_left;
			}

			_node = min;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}

	Self& operator--()
	{
		if (_node->_left)
		{
			Node* max = _node->_left;
			while (max->_right)
			{
				max = max->_right;
			}

			_node = max;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_left)
			{
				cur = parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}

	bool operator!=(const Self& s)const
	{
		return _node != s._node;
	}

	bool operator==(const Self& s)const
	{
		return _node == s._node;
	}
};

//set   PBTree<K, K, SetKeyOfT>
//map   PBTree<K, pair<K, V>, MapKeyOfT>
template<class K, class T, class KeyOfT>
struct RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef RBTreeIterator<T, T&, T*> iterator;
	typedef RBTreeIterator<T, const T&, const T*> const_iterator;

	iterator begin()
	{
		Node* min = _root;
		while (min && min->_left)
		{
			min = min->_left;
		}

		return iterator(min);
	}

	iterator end()
	{
		return iterator(nullptr);
	}

	RBTree()
		:_root(nullptr)
	{}

	RBTree(const RBTree<K, T, KeyOfT>& t)
	{
		_root = Copy(t._root);
	}

	//t1 = t2
	RBTree<K, T, KeyOfT>& operator==(RBTree< K, T, KeyOfT> t)
	{
		swap(_root, t._root);
		return *this;
	}

	~RBTree()
	{
		Destroy(_root);
		_root = nullptr;
	}

	iterator Find(const K& key)
	{
		Node* cur = _root;
		KeyOfT kot;
		while (cur)
		{
			if (kot(cur->_data) < key)
			{
				cur = cur->_right;
			}
			else if (kot(cur->_data)>key)
			{
				cur = cur->_left;
			}
			else
			{
				return iterator(cur);
			}
		}

		return end();
	}

	pair<iterator, bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return make_pair(iterator(_root), true);
		}

		KeyOfT kot;

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return make_pair(iterator(cur), false);
			}
		}

		cur = new Node(data);
		Node* newnode = cur;
		cur->_col = RED;         //新增节点
		if (kot(parent->_data) < kot(data))
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}

		//控制平衡
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				//1.uncle存在且为红
				if (uncle && uncle->_col == RED)
				{
					//变色，继续向上处理
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else	// uncle不存在    存在且为黑					
					//        g
					//     p
					//  c

					//        g
					//     p
					//        c

				{
					if (cur == parent->_left)
					{
						//单旋
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						//双旋
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
			else     //parent == grandfather->_right
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					//变色  继续向上调整
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else     //  uncle不存在   存在且为黑
				{
					//  g    
					//     p
					//        c

					//  g
					//     p
					//  c
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

		_root->_col = BLACK;
		return make_pair(iterator(newnode), true);
	}

private:
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		Node* parentParent = parent->_parent;
		subR->_left = parent;
		parent->_parent = subR;

		if (_root == parent)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
				parentParent->_left = subR;
			else
				parentParent->_right = subR;
			subR->_parent = parentParent;
		}
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		Node* parentParent = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
				parentParent->_left = subL;
			else
				parentParent->_right = subL;

			subL->_parent = parentParent;
		}
	}

	void Destroy(Node* root)
	{
		if (root == nullptr)
			return;

		Destroy(root->_left);
		Destroy(root->_right);
		delete root;
	}

	Node* Copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;

		Node* newRoot = new Node(root->_data);
		newRoot->_col = root->_col;

		newRoot->_left = Copy(root->_left);
		newRoot->_right = Copy(root->_right);
		if (newRoot->_left)
			newRoot->_left->_parent = newRoot;

		if (newRoot->_right)
			newRoot->_right->_parent = newRoot;

		return newRoot;
	}

private:
	Node* _root;
};