本文是对Jeff Erickson经典算法入门书籍《Algorithms》中动态规划问题的阅读笔记,近期在刷一些编程题,对于如何凑出动态规划更新的范式,脑袋里一直是一团乱麻,特别看完了别人的题解,只是惊叹其脑洞,但一直搞不清其是怎么想出来的。《Algorithms》给出了动态规划解决的非常清晰的思路,从递归出发,一步步完成动态规划更新的范式的推理。本文结合个人理解作了总结。
Jeff指出动态规划本质上是没有重复计算的递归问题,递归算法将原问题拆解为缩小的子问题,而动态规划在于设计合理的递归路径,保存之前已经计算好的子问题的结果,从而减少未来的重复计算。
本文结合了Jeff的步骤,总结了动态规划问题的一般性实现步骤:
- A) 定义递归形式:将父问题拆分为子问题和问题边界,并由递归来定义原问题
,其中
表示数据量更小的子问题。
- B) 展开递归路径:确定由子问题到父问题的解决路径。
- C) 确定合适的执行顺序:保证父问题所有依赖的子问题都在其执行前完成。
- D) 确定合适的数据结构保存子问题的结果:保存的结果是父问题计算所依赖的,可以采用数组、矩阵、树等等,数据结构的访问一般同问题执行顺序相适配。
- E) 确定问题边界和问题计算逻辑:根据递归问题的边界条件来初始化数据结构,同时将递归形式转化了动态规划的计算问题。
- F) 对时间和空间的优化分析:分析空间和时间复杂度,同时分析在执行路径和存储数据结构中是否有冗余。
接下来,我们将举一些例子,展开讨论下通过上述步骤如何解决动态规划问题。
1. 斐波那契Fibonacci问题
A) 定义递归形式:
第n个斐波那契数可以定义为递归的形式,即,问题边界
。此时可以很容易写出如下递归代码:
def Fibonacci(n):
if n <= 2:
return 1
return Fibonacci(n-1) + Fibonacci(n-2)B) 展开递归路径:
我们将上述递归过程展开成如下执行路径,我们发现存在大量的重复计算,比如F(3)的分支在F(4)、F(5)、F(6)等中都有重复计算。
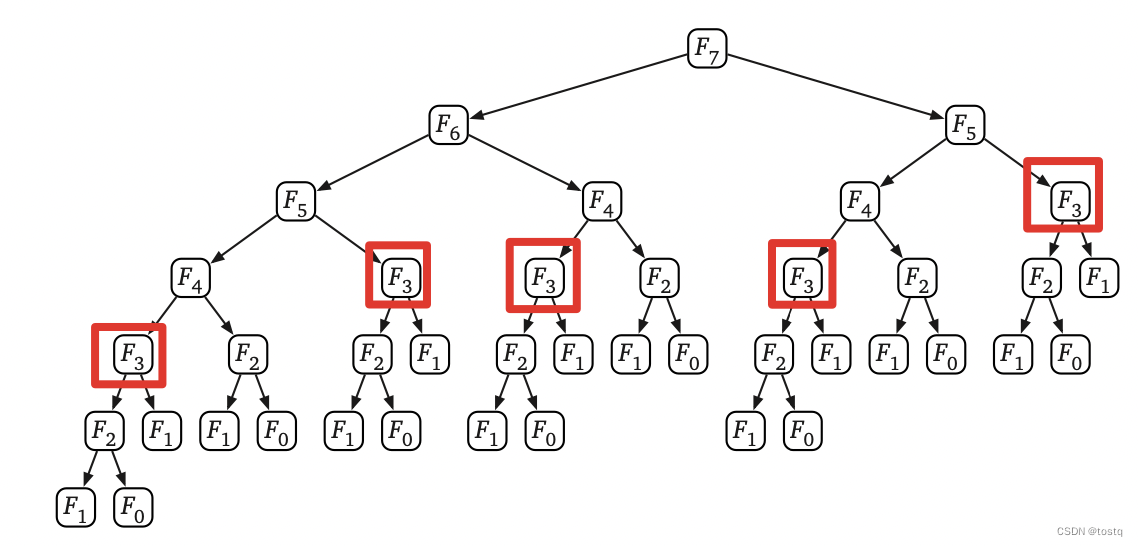
C) 确定合适问题执行顺序
我们按n=1,2,3,…,N的顺序来计算,就能保存F(n)的所有依赖的子问题F(n-1) 和F(n-2)都在其执行前完成计算。
D) 确定合适的数据结构保存子问题的结果
我们可以采用数组的形式来保存子问题的结果,比如D[n]表示F(n)的结果。
E) 确定问题边界和问题计算逻辑
此时我们可以写出动态规划的代码
def Fibonacci(n):
D=[0 for i in range(n+1)]
D[1], D[2]=1, 1
for i in range(3, n + 1):
D[i]=D[i-1]+D[i-2]
return D[n]F) 对时间和空间的优化分析
通过上述的代码可以发现,实际并不需要一个数组来保存全部的结果,只需要3个变量就可以完成。
def Fibonacci(n):
D1, D2 = 1, 1
for i in range(3, n + 1):
D3 = D1 + D2
D1 = D2
D2 = D3
return D3另外也可以发现在执行上是否不需要遍历n个,确实是的,最优的执行时间复杂度为,Jeff的原文给出了具体的方法,本文不再列出了。接下来,我们考虑更为复杂的问题
2. 正则匹配的问题
正则匹配问题定义为:
给定一个字符串 (s) 和一个字符模式 (p) ,实现一个支持 '?' 和 '*' 的通配符匹配。
'?' 可以匹配任何单个字符。
'*' 可以匹配任意字符串(包括空字符串)。
两个字符串完全匹配才算匹配成功。
说明:
- s 可能为空,且只包含从 a-z 的小写字母。
- p 可能为空,且只包含从 a-z 的小写字母,以及字符 ? 和 *。
A) 定义递归形式:
首先我们仍然是定义问题的递归形式,我们先将问题拆解成如下的子问题情况:
- 当s[0]和p[0]完全匹配,此时s[0]和p[0]都是字母,此时我们只需要判断s[1:]和p[1:]是否是匹配
- 当p[0]是?,对应肯定匹配s[0],此时也只需要判断s[1:]和p[1:]是否是匹配
- 当p[0]是*,此时对应三种情况为空,只同s[0]匹配,同s[0]匹配
我们用代码描述上述过程更为清晰,isMatch函数是要解决问题函数,其判断输入s和p是否是正则匹配(True or False)
if s[0] == p[0]:
return isMatch(s[1:], p[1:])
elif p[0] == "?":
return isMatch(s[1:], p[1:])
elif p[0] == "*":
return isMatch(s[1:], p[1:]) or isMatch(s[1:], p) or isMatch(s, p[1:])
return False我们再考虑递归问题的边界:
- 当s和p均为空的情况下,返回True
- 当只s为空的情况下,p为空或者持续为*的情况,返回True否则为False
- 当只p为空的情况下,返回False
if len(s) == 0:
if p.strip("*") == "":
return True
else:
return False
elif len(p) == 0:
return FalseB) 展开执行路径:
通过上面的分析,可以知道递归问题的依赖顺序可以表示为如下,此处的i,j分别代表s[i:],p[j:],F(i,j)表示s[i:],p[j:]是否是正则匹配。
C) 确定合适的执行路径:
执行顺序可以为如下,其中和
分别表示s和p的长度,此时能满足所有F(i,j)所依赖的子问题在其执行前完成执行。
D) 确定合适的数据结构保存子问题的结果:
我们可以采用矩阵的形式来保存子问题的结果,比如M[i][j]表示F(i,j)的结果,即s[i:],p[j:]是否是正则匹配。
E) 确定问题边界和问题计算逻辑:
- 当
时即s为空,并且当
时即p为空,M[i][j] = True
- 仅当
时,p持续为*时为True,否则为False
- 仅当
时,M[i][j] = False
M = [[False for j in range(len(p) + 1)] for i in range(len(s) + 1)]
for j in range(len(p), -1, -1):
if j == len(p) or p[j] == “*”:
M[len(s)][j] = True
else:
breakM的计算逻辑,参考原来的递归问题的处理结构:
if s[i] == p[j]:
M[i][j] = M[i-1][j-1]
elif p[j] == "?":
M[i][j] = M[i-1][j-1]
elif p[j] == "*":
M[i][j] = M[i-1][j-1] or M[i-1][j] or M[i][j-1]
else:
M[i][j] = False最终完成代码如下:
def isMatch(s, p):
M = [[False for j in range(len(p) + 1)] for i in range(len(s) + 1)]
for j in range(len(p), -1, -1):
if j == len(p) or p[j] == "*":
M[len(s)][j] = True
else:
break
for i in range(len(s) - 1, -1, -1):
for j in range(len(p) - 1, -1, -1):
if s[i] == p[j]:
M[i][j] = M[i+1][j+1]
elif p[j]== "?":
M[i][j] = M[i+1][j+1]
elif p[j] == "*":
M[i][j] = M[i+1][j+1] or M[i+1][j] or M[i][j+1]
else:
M[i][j] = False
return M[0][0]