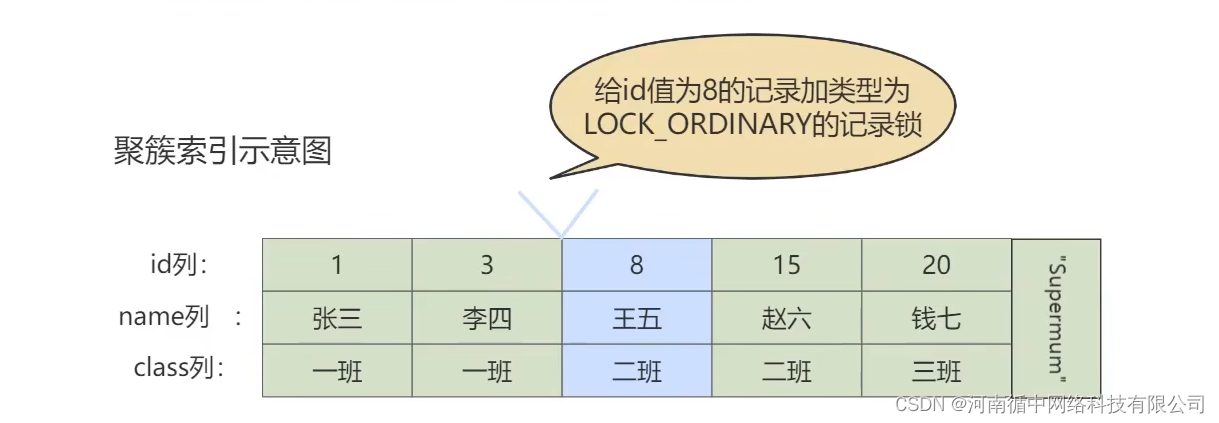
回溯

将 $2$——$9$ 和字母对应起来，用字符串数组保存。

递归遍历 $digits$ 每一个数字，每一个数字对应的字母，又可以递归遍历，和下一个数字的字母组成排列。当排列长度等于 $digits$ 的长度，就组成了一个排列。

$dfs$ 树 ， 以 $digits=2/3/4$ 为例

只画出了部分 $dfs$ 树，$b$ 和 $c$ 的子树可以参考 $a$ ，一共 $3^3=27$ 种组合。

代码展示

class Solution {
public:
    string strs[10]{
        "","","abc","def",
        "ghi","jkl","mno",
        "pqrs","tuv","wxyz",
    };
    vector<string> ans ;
    vector<string> letterCombinations(string digits) {//回溯法
        if(digits.empty()) return ans;//输入空，返回空。
        dfs(digits,0,"");
        return ans;
    }
    void dfs(string digits, int u , string path){//u在path对应第几个字符。
        if(u==digits.size()) ans.push_back(path);
        else{
            for(char &x:strs[digits[u]-'0'])//u在digits对应第几个数字。
                dfs(digits,u+1,path+x);
        }
    }
};

博主致语

理解思路很重要！
欢迎读者在评论区留言，作为日更博主，看到就会回复的。

AC

复杂度分析

1. 时间复杂度: $O(4^n\times n)$， $n$ 是 $digits$ 的长度 ， 每个数字最多对应 $4$ 个字母 ， 递归组合，最坏时间复杂度$O(4^n)$，$push\_back$ 的时间复杂度 $O(n)$ ，综上，最坏时间复杂度$O(4^n)$。
2. 空间复杂度: $O(n)$，压栈最大深度 $n$ ，对应的空间复杂度 $O(n)$ 。