🌼 扎着马尾的姑娘,笑容温柔很善良
自在的少年 - 要不要买菜 - 单曲 - 网易云音乐
前言
本来打算做蓝桥杯2022C++A组省赛F题青蛙过河的,看到标签显示"二分",第一时间竟然想不到二分是什么,所以来学习下
目录
🌼二分是什么
🌼一,砍树
🌼二,手写快排
🌼三,阶乘末尾0的个数
🌼四,序列合并
代码1 优先队列
代码2 二分
🌼五,银行贷款
🌼总结
🌼二分是什么
概念
部分知识来自 二分 - OI Wiki (oi-wiki.org)
挺好的算法搜索网站,大家可放到收藏夹,专门搜算法用
二分查找(binary search),也称折半搜索(half-interval search)或对数搜索(logarithmic search)
用来在有序数组(单调增减)中查找某一元素的算法
比如,在升序数组中
每次查找当前部分中间元素,如果中间元素是要找的,结束搜索
如果小于所查找的值,左侧只会更小,所以在右侧查找
如果大于,则在左侧查找
二分查找最优时间和空间复杂度都是O(1),最差时间和空间复杂度都是O(logn)
模板
模板只提供一个思路,不能照搬
int binary_search(int left, int right, int key)
{
int ret = -1; //未搜索到数据返回-1下标
int mid;
while(left <= right) {
mid = left + ((right - left) >> 1); //避免溢出,用该算法
if(key > a[mid]) left = mid + 1;
else if(key < a[mid]) right = mid - 1;
else { //最后检测相等
ret = mid;
break;
}
}
return ret; //单一出口
}对于一个长度为n的数组,若n是有符号数,当n >= 0, n >> 1比 n / 2更快,且只能用于整数
使用条件
1,有序(广义有序,查找满足某种条件的最大最小值)
2,比如要找最大值,首先想到从小到大枚举,若答案单调,可使用二分提高效率
3,固定区间; 判断某个值是否符合条件; 可行解对于区间满足一定单调性
题目加深理解
🌼一,砍树
P1873 [COCI 2011/2012 #5] EKO / 砍树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)


标签: 二分, 普及/提高-
1,可以在1~10^9枚举,但是这种朴素写法会超时,只适合在蓝桥杯骗分
2,可以sort()排序再优化砍多少米
3,由于要学习二分,我们采用二分
发现的问题
1,right不要声明为全局变量,会与#include<iostream>库里的属性或方法重名
2,大数组,比如long long a[1000010]; 要声明在主函数外作为全局变量,因为主函数内用栈存储,栈的空间没那么大,会溢出,导致调试时,无法输入,而全局变量在静态存储区分配,空间很大
3, left <= right right = mid - 1 mid + 1 printf("%lld", mid - 1)这几行代码,需要自己多弄几组数据测试
否则会出现Ac30% 或50%等情况
4,最好将所有整型声明为long long,避免后续操作导致的溢出(注意,因为习惯性int i ,可能出错)
代码1 AC50%
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
long long n, m, sum, mid, a[1000010];
int main()
{
long long right = 0, left = 0; //初始左右边界
scanf("%lld%lld", &n, &m);
for(int i = 0; i < n; ++i) {
scanf("%lld", &a[i]);
right = max(a[i], right); //最高的树作为初始右边界
}
while(left <= right) {
sum = 0; //更新
mid = (left + right) >> 1; //mid为伐木高度
for(int i = 0; i < n; ++i)
if(a[i] > mid) sum += a[i] - mid;
if(sum < m) right = mid - 1;
else left = mid + 1;
}
printf("%lld", mid - 1);
return 0;
}
代码1过了两个样例,但是在下面例子中输出了0,应该输出1才是
5 20
1 3 5 7 10问题出在最后的printf(),不是mid - 1(50%),不是mid(50%),也不是left(wa),是right(100%)
代码逐行解析:
mid为伐木高度,但不是最终输出答案
left左边界,right右边界,数组a存储所有树木高度
sum为砍伐后获得树木总长度
关键1
第16行mid = (left + right) >> 1等价于mid = (left + right) / 2,位运算速度更快
关键2
第19~20行right = mid - 1和left = mid + 1
这三行实现了砍树高度的二分
由于题目要求的是,刚好能得到>=m米木材的临界点,所以输出right
Ac 100%代码
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
long long n, m, sum, mid, a[1000010];
int main()
{
long long right = 0;
scanf("%lld%lld", &n, &m);
for(int i = 0; i < n; ++i) {
scanf("%lld", &a[i]);
right = max(a[i], right); //最高的树作为初始右边界
}
long long left = 0; //初始左边界
while(left <= right) {
sum = 0; //更新
mid = (left + right) >> 1; //mid为伐木高度
for(int i = 0; i < n; ++i)
if(a[i] > mid) sum += a[i] - mid;
if(sum < m) right = mid - 1;
else left = mid + 1;
}
printf("%lld", right);
return 0;
}
🌼二,手写快排
P1026 - 排序 - New Online Judge (ecustacm.cn)
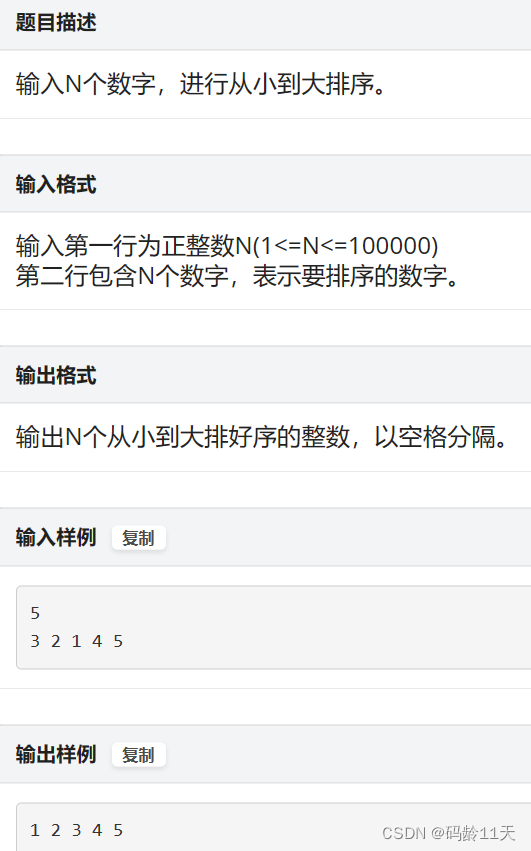
标签: 入门题
因为快排 = 二分 + 递归,所以通过再次手写快排加深对二分的理解
快速排序最好的时间复杂度和二分平均时间复杂度一样,都是O(logn),而最差时间复杂度为O(n^2)
#include<iostream>
using namespace std;
int a[100010]; //声明为全局,不用传参
void quick_sort(int left, int right)
{
if(left > right) return;
int i = left, j = right, base = a[left];
while(i < j) {
while(i < j && a[j] >= base) j--; //j游标先行
while(i < j && a[i] <= base) i++; //i游标后走
//退出上面两循环后,i,j分别指向大于base和小于base的值
if(i < j) {
a[i] = a[i]^a[j];
a[j] = a[i]^a[j];
a[i] = a[i]^a[j]; //异或交换两数
}
}
a[left] = a[j]; //j先行,此时i,j指向的元素必要小于基数
a[j] = base; //交换完毕后,左边都小于base,右边都大于base
quick_sort(left, j - 1); //对左边递归
quick_sort(j + 1, right); //对右边递归
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; ++i) cin>>a[i];
quick_sort(0, n - 1);
for(int i = 0; i < n; ++i) cout<<a[i]<<" ";
return 0;
}
核心代码也就十几行
🌼三,阶乘末尾0的个数
(一)标签:入门题
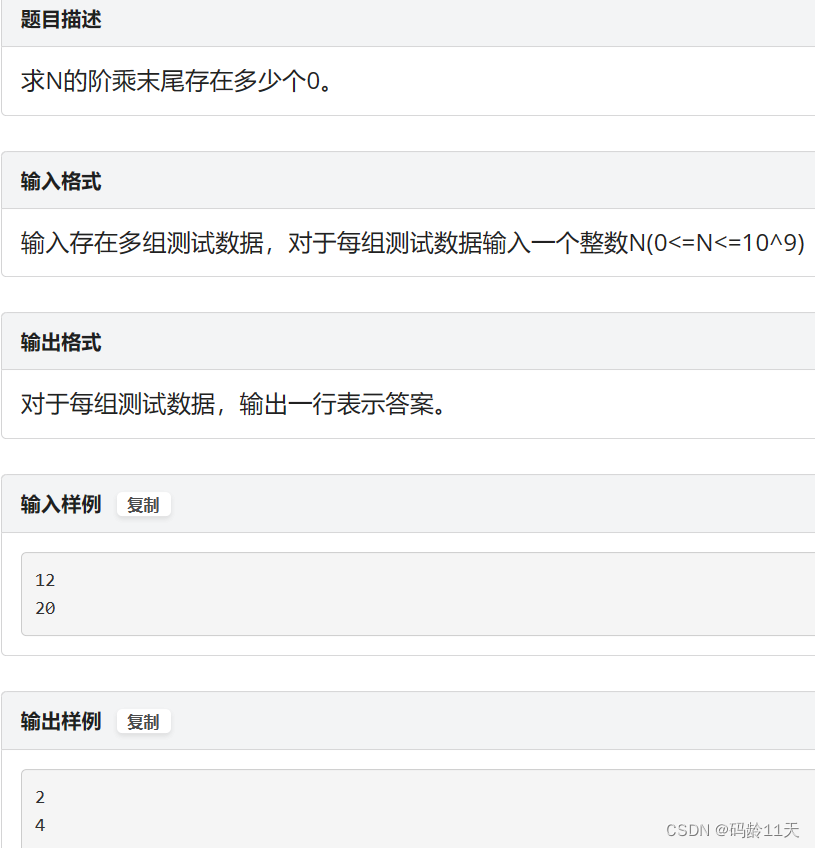
因为n!中的n可达10^9,直接递归肯定超时,我们转换个思路
1,求0的个数,也就是求n!能被10整除多少次
2,由于10 = 5 * 2,5 * 任意偶数都能得到10
3,所以转化为求n中5因子的个数
#include<iostream>
using namespace std;
int main()
{
long long n;
while(cin>>n) {
int sum = 0; //sum = 0要放在外层while里
while(n) {
sum += n / 5;
n /= 5;
}
cout<<sum<<endl;
}
return 0;
}
(二)标签:基础题,二分
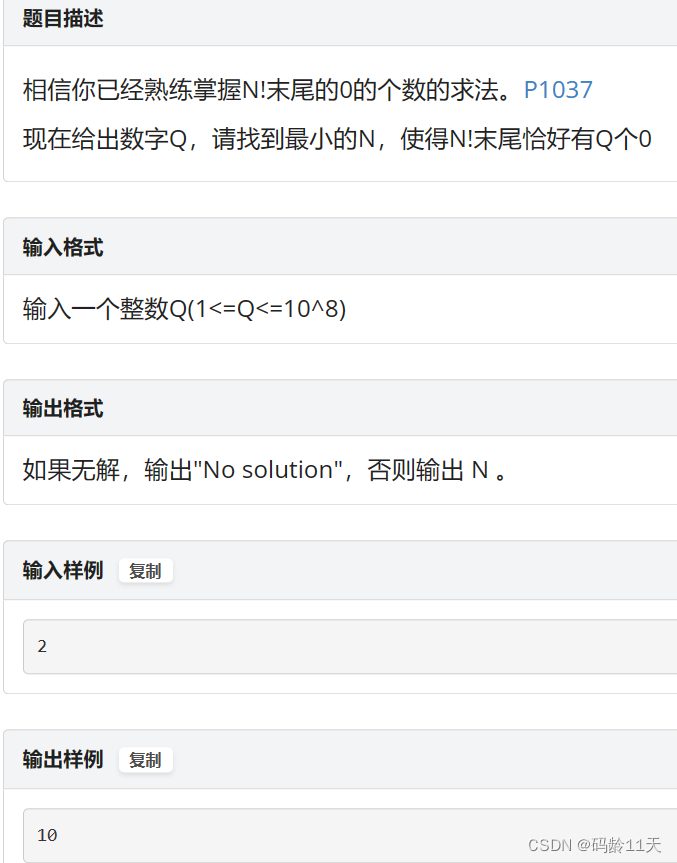
首先,基于上一题,我们可以写个函数求n!中0的个数
其次,想要用二分来提高效率,首先得明确右边界,就是最大值
容易知道 100! 有24个0,同理 1000! 大约有240个0,所以要求10^8个0,大约得4*10^8阶乘
所以右边界给它算10^12,往大了开,反正long long到10^8
有一个坑,题目要求的是最小的N,比如输入2后,10!和12!都有2个0,这时你输出13就不对,因为不是最小的
第一次好歹还能输出个答案,虽然不是最小N,为了输出最小N,我加了一个限制条件,就输出了一堆屁
一堆屁
#include<iostream>
using namespace std;
long long q, flag = 1, ans, temp;
long long zero(long long n)
{
int sum = 0;
while(n) {
sum += n / 5;
n /= 5;
}
return sum;
}
long long check(long long q)
{
long long left = 0, right = 1000000000000, mid; //10^12
while(left <= right) {
mid = (left + right) >> 1; //中间值
if(zero(mid) < q) left = mid + 1;
else if(zero(mid) > q) right = mid - 1;
else {//检测相等
return mid;
}
}
}
int main()
{
cin>>q;
while(1) {
ans = check(q);
temp = ans;
while(zero(--temp) == q) ans--;
cout<<ans;
break;
}
return 0;
}
2
429496729635以前也遇到过类似情况,一时想不起来了
思路:同样是上一个代码的想法,找 n! 中 0 的个数,就是求 n 中 因子5的数量,忽略了这个思路,代码就复杂许多,各种出错AC不了不足为奇
AC代码之❌
#include<cstdio> //scanf(), printf()
long long zero(long long n)
{
long long sum = 0;
while(n) {
sum += n / 5;
n /= 5;
}
return sum; //0的个数
}
int main()
{
long long q;
scanf("%lld", &q);
for(int i = 1;; ++i) {
if(zero(i * 5) == q) { //遍历时只需对5的倍数遍历即可
printf("%lld", i * 5);
break;
}
else if(zero(i * 5) < q && zero(i * 5 + 5) > q) {
printf("No solution");
break;
}
}
return 0;
}
2
-8589934582发现问题了吗,代码第15行,int i放入zero(long long)是不匹配的
AC代码之 ✔
#include<cstdio> //scanf(), printf()
long long zero(long long n)
{
long long sum = 0;
while(n) {
sum += n / 5;
n /= 5;
}
return sum; //0的个数
}
int main()
{
long long q;
scanf("%lld", &q);
for(long long i = 1;; ++i) {
if(zero(i * 5) == q) { //遍历时只需对5的倍数遍历即可
printf("%lld", i * 5);
break;
}
else if(zero(i * 5) < q && zero(i * 5 + 5) > q) {
printf("No solution");
break;
}
}
return 0;
}
不用二分了,有点麻烦,,,但是锻炼的效果已经达到了(好歹写了一堆屁出来)
🌼四,序列合并
P1102 - 序列合并 - New Online Judge (ecustacm.cn)
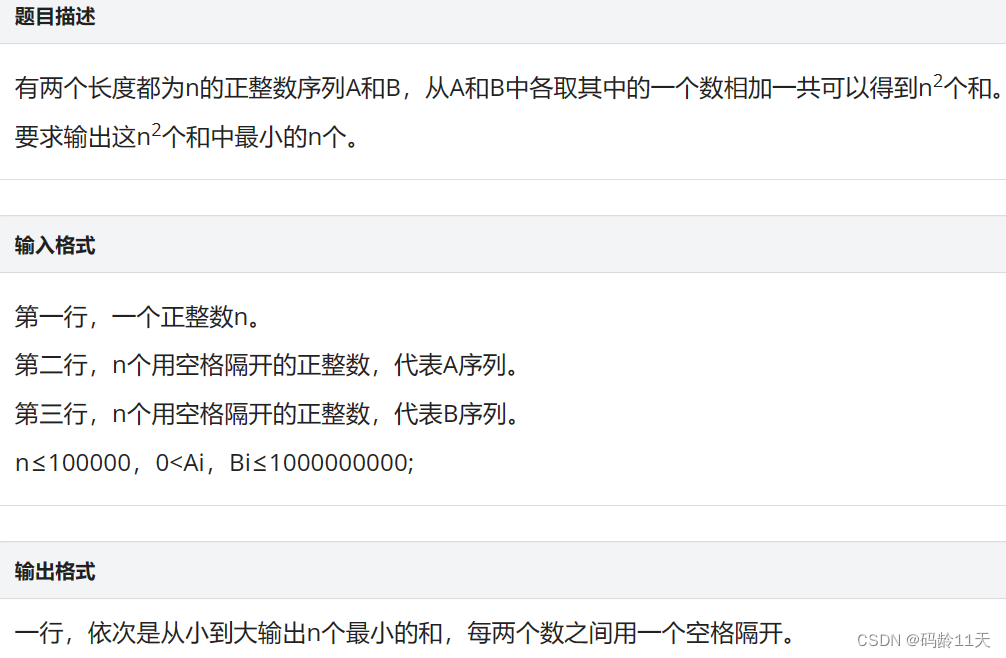
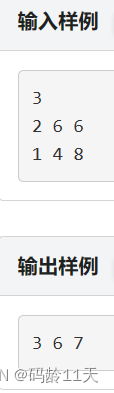
标签:基础题,二分
可以用优先队列,也可以用二分
思路1 优先队列
我也第一次接触,先来个科普文
(6条消息) C++优先队列priority_queue详解_是一只派大鑫的博客-CSDN博客_priority_queue头文件
因为要输出前n个最小值,利用优先队列自动排序的特点很好做
默认是最大值优先队列,即最大值在顶端
priority_queue<int,vector<int>,less<int>>p2;//最大值优先队列
priority_queue<int,vector<int>,greater<int>>p3;//最小值优先队列在这里,我们作个比较,栈的声明是这样的:
#include<stack> //st.pop(), st.push()
int main()
{
stack<int>st;
}而优先队列的声明,是这样的:
(注意,#include<queue>和using namespace std;两行要配合使用)
#include<queue>
using namespace std;
int main()
{
priority_queue<int>q;
}核心代码第24,25行,利用了最大值优先队列中,最大值始终在队首的特点
代码第17,18行,对数组a, b排序,是为了第27行可以break,不至于超时
代码1 优先队列
#include<cstdio> //scanf(), printf()
#include<algorithm> //sort()
#include<queue> //1
using namespace std; //2
int a[100010], b[100010];
int main()
{
priority_queue<int>q; //3
int n, i, j;
scanf("%d", &n);
for(i = 0; i < n; ++i)
scanf("%d", &a[i]);
for(i = 0; i < n; ++i)
scanf("%d", &b[i]); //输入
sort(a, a + n);
sort(b, b + n); //排序
for(i = 0; i < n; ++i) q.push(a[0] + b[i]); //入队n个元素
for(i = 1; i < n; ++i)
for(j = 0; j < n; ++j) {
if(a[i] + b[j] < q.top()) {
q.pop(); //核心代码
q.push(a[i] + b[j]); //核心代码
}
else break; //后面必定更大,可以直接break
}
//最大值优先队列,最大值在顶端,所以逆序保存
for(i = n - 1; i >= 0; --i) {
a[i] = q.top(); //最大值放最后
q.pop(); //出队
}
for(int i = 0; i < n; ++i)
printf("%d ", a[i]);
return 0;
}
---------------------------------------------------------------------------------------------------------
思路2 二分
代码中两层for遍历时,出现2次else break; 这步很重要,因为排序后单调递增,所以后续没必要比较,不用就超时
第二,由于要使用二分,加上单个数10^9,右边界最大2*10^9,左边界最大也可能接近2*10^9,所以相加时int会超限,所以用long long
当然,也可以mid = left + (right - left) >> 1,这样用int也是可以的
第一次敲出来后,在第40行报错 error: invalid types long long int ... ... for subscript
百度说
1,数组变量名敲错 / 未定义
2,数组超限
3,变量名数组名重复定义
4,个人变量名与C++库的变量名冲突
if(a[i][j] <= right) c[num++] = a[i][j];原来是把a[i] + b[j]写成了a[i][j]🤦
注意!!! 不要照搬模板,比如下面核心代码中,第33,35,36行,
第33行要left < right,如果加上 = 会时间超限 AC 0%
第35,36行,如果改成right = mid, left = mid会超限并AC 20%
代码2 二分
#include<iostream>
#include<cstdio> //scanf(), printf()
#include<algorithm> //sort()
using namespace std;
typedef long long LL;
LL a[100010], b[100010], c[100010], n, i, j;
bool check(long long x) //return false这样的,用bool
{
LL ans = 0;
for(i = 0; i < n; ++i)
for(j = 0; j < n; ++j) {
if(a[i] + b[j] <= x) ans++;
else break; //这步很重要
if(ans == n) return true; //x可能小了
}
return false; //x大了
}
int main()
{
scanf("%d", &n);
for(i = 0; i < n; ++i)
scanf("%lld", &a[i]); //lld
for(i = 0; i < n; ++i)
scanf("%lld", &b[i]); //lld
sort(a, a + n);
sort(b, b + n);
//初始左右边界
LL left = a[0] + b[0], right = a[n - 1] + b[n - 1];
//二分核心代码
while(left < right) { //<
LL mid = (left + right) >> 1;
if(check(mid)) right = mid - 1; //mid - 1
else left = mid + 1; //mid + 1
}
LL num = 0;
for(i = 0; i < n; ++i)
for(j = 0; j < n; ++j) {
if(a[i] + b[j] <= right) c[num++] = a[i] + b[j];
if(num == n) break;
}
sort(c, c + n);
for(i = 0; i < n; ++i) printf("%lld ", c[i]); //记得用lld
return 0;
}
🌼五,银行贷款
P1163 银行贷款 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
如果是正向(提供月利率求还清款项的月数),很简单
无奈本题反向,需要二分,无非就是写个正向的check()函数,主函数里二分即可
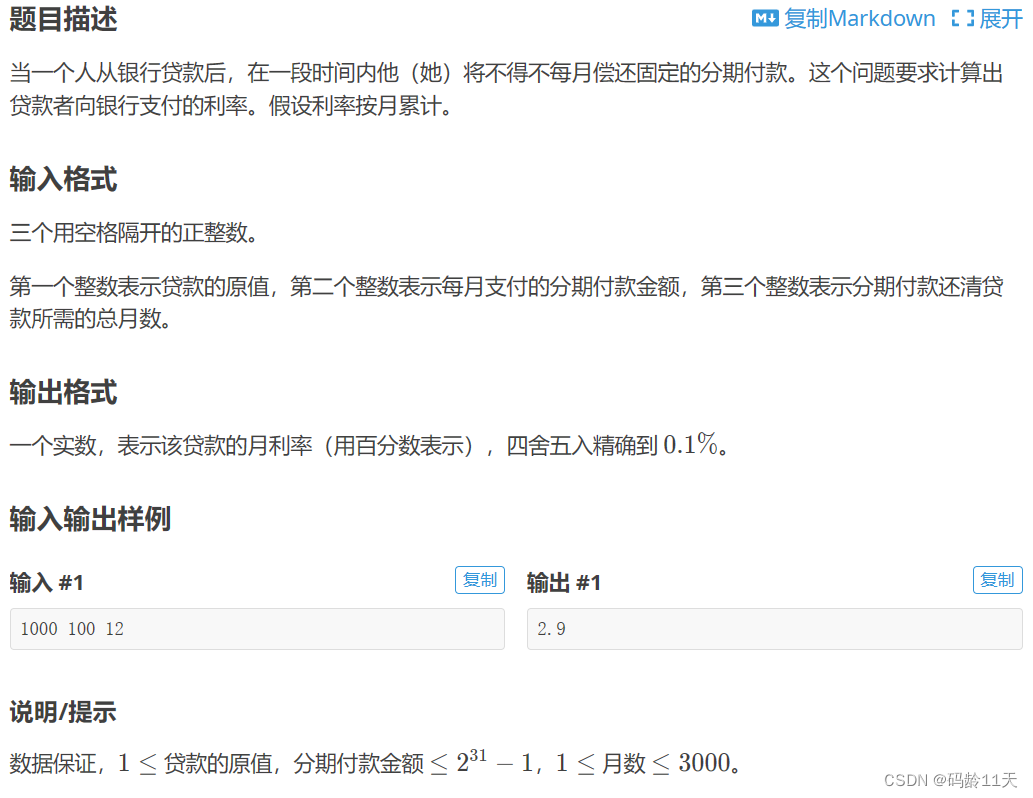
标签:普及-,数学,二分
第一次敲出来了,但输出不对,debug半小时也没找到原因,写写改改太混乱了,所以重写
需要注意的是
1,先计算复利再还钱(第一个坑)
2,printf()输出双精度要用%f,不能用%lf (第二个坑)
3,因为求得是百分数,最后的mid要*100
AC 代码
#include<cstdio> //scanf()
using namespace std; //cout
double debt, p, num; //欠款, 每月还款, 还清月数
double check(double m) //monthly interest月利率
{
double d = debt, pp = p, n = num;
while(n--) {
d += d * m; //先计算复利, += 欠债 * 月利率
d -= pp; //再还钱, -= 每月还款
}
return d; //返回剩余欠款
}
int main()
{
scanf("%lf%lf%lf", &debt, &p, &num);
double left = 0, right = 10; //1000%
while(1) {
double mid = (left + right) / 2;
if(check(mid) < 0) left = mid;
if(check(mid) > 0) right = mid;
if(check(mid) == 0 || right - left < 0.0001) //精度
{
printf("%.1f", mid * 100); //输出%f就好
break;
}
}
return 0;
}
🌼总结
1,了解了二分模板和概念,比如使用于有序数组,比如明确左右边界
2,加强了对枚举遍历骗分的认识
3,大数组要声明为全局变量,long long可防止后续操作爆int
4,有简便方法就换简便方法,思路一变天地宽
5,输入的数,要与函数形参的类型对应
6,优先队列的声明
#include<queue>
using namespace std;
priority_queue<int>q; //默认最大值优先队列priority_queue<int,vector<int>,less<int>>p2;//最大值优先队列
priority_queue<int,vector<int>,greater<int>>p3;//最小值优先队列7,二分遇到不需要再比较的情况,及时break
8,printf()输出双精度,%f就行,%lf不行