计算机视觉读书笔记|相机内外参及相机标定,矫正的重要性
这篇博客将介绍针孔成像,透镜(弥补了针孔成像曝光不足成像速度慢的缺点,但引进了畸变,主要是径向畸变和切向畸变,径向畸变主要是离中心越远越弯曲,切向畸变当透镜与成像目标不平行时导致),相机内外参(内参4个矩阵参数,5个畸变参数;外参6个,3个旋转向量,3个平移向量)及相机标定,矫正的重要性及目的,主要是为了矫正畸变及三维重建。
1. 针孔成像及透镜
从发射源发出的射线形成光线,然后穿过空间照射到某些物体上。照射到物体上的大部分光线被物体表面吸收。而只有少部分没有吸收的光线被我们所察觉到,并形成光线的颜色。
光线从物体发射开始,通过透镜到达眼睛或摄像机,然后到达视网膜或者图像采集器。
不选用针孔而选用透镜的原因是,真实的针孔不能为快速曝光收集足够的光线。
但使用透镜带来了畸变。
可以利用 摄像机标定(camera calibration) 来矫正因使用透镜而给针孔模型带来的主要偏差。以及从摄像机的二维自然单位(像素)和物体世界的单位(米)的关系来进行3维场景的重构。
摄像机标定的过程既给出摄像机几何模型,也给出透镜的畸变模型。这俩个模型定义了摄像机的内参数(intrinsic parameter)。
单应变换(homograph transform)是一种能够描述摄像机基本行为特性和各种失真、矫正特性的数学工具。
投影平面project plane
焦距focal length,从针孔到屏幕的距离就是焦距f。
Z是摄像机到物体的距离
X是物体长度
x是图像平面上的物体图像
则-x/f = X/Z 即:-x = FX/Z
针孔点被理解为投影中心center of projection
光轴与图像屏幕的交点被称为主点principle point
x/f = X/Z
针孔摄像机成像图如下:
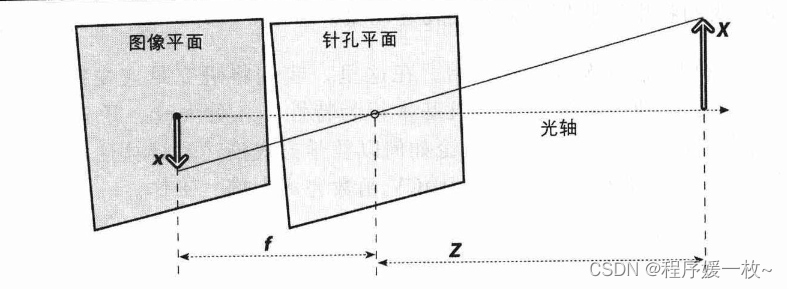
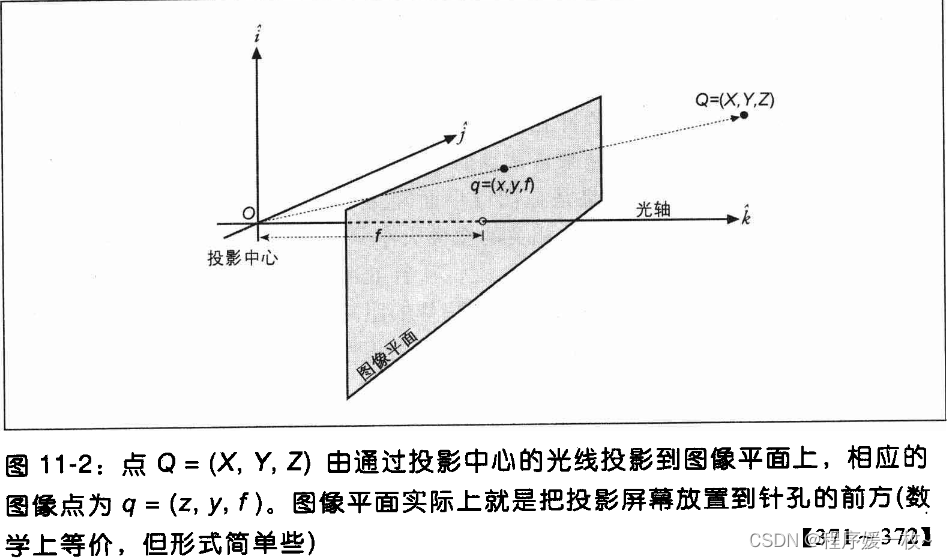

由于只有少量的光线通过针孔,导致因曝光不足而使得图像生成得很慢。对于要快速生成图像的摄像机而言,必须利用大面积且弯曲的透镜,让足够多的光线收敛聚集到投影点上。(透镜可以据集足够多的光线到某个点上,使得图像生成更加迅速,其代价就是引入了畸变。)
2. 径向畸变和切向畸变
径向畸变来自于透镜形状,而切向畸变则来自于整个摄像机的组装过程。

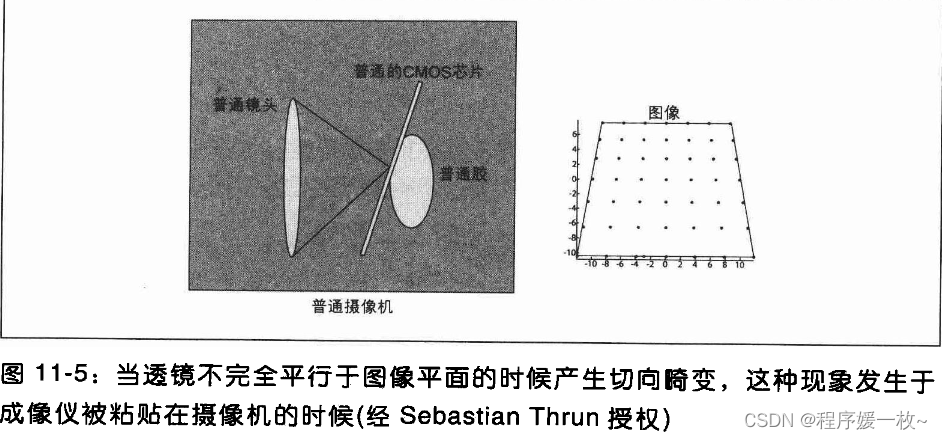
标定物(calibration object)
平面的单应性被定义为从一个平面到另一个平面的投影映射。单应性矩阵H。
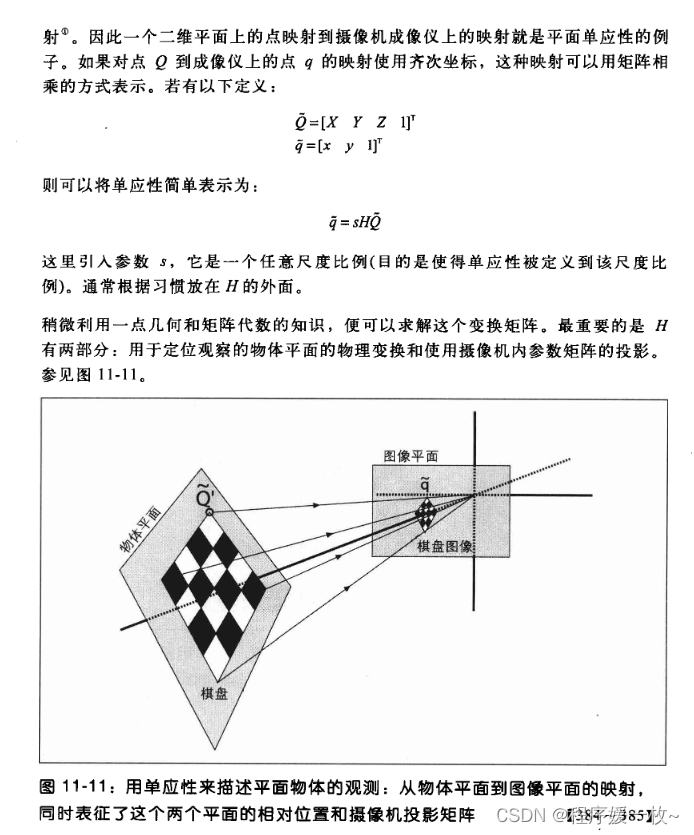
3. 相机的内外参及标定函数
内参:
有4个内参数(fx,fy,cx,cy)和 5个畸变参数——3个径向(k1,k2,k3)和俩个切向(p1,p2);
内参数直接与棋盘所在空间的3D几何相关(即外参数),而畸变参数则与点集如何畸变的2D集合相关。
内参数矩阵,也称为摄像机矩阵M,如下:

外参:
相机外参矩阵描述的是相机在静态场景下相机的运动,包括旋转和平移,或者在相机固定时,运动物体的刚性运动。
有3个轴的旋转参数(ω、δ、 θ)和平移参数(Tx,Ty,Tz),旋转矩阵R,平移向量T
-
内参数矩阵完全定义了理想摄像机模型的摄像机行为,而畸变参数则更多表征摄像机的非理想行为。
摄像机矩阵总是3X3的,而畸变系数总是5个,记录顺序是:k1,k2,p1,p2,k3 -
外参数概括的是对于摄像机来说标定物体的位置,由三维空间3个坐标轴的旋转和平移向量表征;
向量长度表示逆时针的旋转角度。平移向量是摄像机坐标系中相对棋盘原点的偏移量。
利用标定函数,可以根据多个图像的角点,来计算相机的内外参:

标定摄像机通常是做俩件事,一个是校正畸变效应,另一个是根据获得的图像重构三维场景。
基本方法是先计算畸变映射,再矫正图像。
参考
- http://www.vision.caltech.edu/bouguetj/calib_doc/
- https://blog.csdn.net/qq_41743157/article/details/124863365


![[附源码]SSM计算机毕业设计智能视频推荐网站JAVA](https://img-blog.csdnimg.cn/5373a83253d541b7a94f872a17867d2e.png)