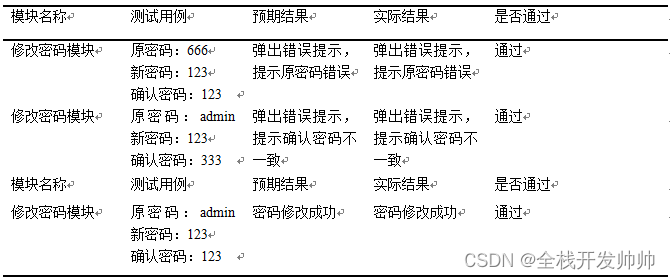
在这里插入代码片## 线性模型
机器学习中的线性模型是一种预测模型，它基于线性关系来预测输出值。这种模型假设输入特征（自变量）和输出（因变量）之间存在线性关系。线性模型通常具有以下形式：

y = x*w + b

其中：

• y 是要预测的输出值。
• x 是输入特征。
• b 是模型的偏置项（bias），可以理解为当所有特征都为零时的输出值。
• w 是模型参数（weights），表示每个特征对输出的影响程度。

如下图所示，先不考虑b的形况下，绘图

然后计算loss（也就是误差）

代码：

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

def forward(x):
    return x*w 

def loss(x,y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y) 

w_list = []
mse_list = []
 
for w in np.arange (0.0, 4.1, 0.1):
   print('w=',w)
   l_sum =0
   for x_val,y_val in zip( x_data,y_data ):
       y_pred_val =format(x_val)
       loss_val = loss(x_val,y_val)
       l_sum += loss_val
       print('t',x_val,y_val,y_pred_val,loss_val)
   print('MSE', l_sum/3)
   w_list.append(w)
   mse_list.append(l_sum/3)
   
plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

结果图：

考虑偏置B

代码：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

def forward(x):
    return x*w + b

def loss(x,y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y) 


mse_list = []
W = np.arange(0.0, 4.1, 0.1)
B = np.arange(0.0, 4.1, 0.1)
[w,b] = np.meshgrid(W,B)

l_sum = 0
for x_val,y_val in zip( x_data,y_data ):
       y_pred_val = forward(x_val)
       print(y_pred_val)
       loss_val = loss(x_val,y_val)
       l_sum += loss_val

fig = plt.figure()
#ax = Axes3D(fig)
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(w, b, l_sum /3)
plt.show()

效果图：

线性模型可以进一步细分为几种类型：

1. 简单线性回归：只有一个特征和一个输出变量。
2. 多元线性回归：有多个特征和一个输出变量。
3. 逻辑回归：虽然名字中有“回归”，但它实际上是一种分类算法，用于二分类问题，输出的是概率。

线性模型的优点包括：

• 简单易懂，易于实现。
• 计算效率高，尤其是在特征数量不多的情况下。
• 可以提供可解释的模型参数，有助于理解特征对输出的影响。

然而，线性模型也有一些局限性：

• 它假设特征和输出之间存在线性关系，这在现实世界中并不总是成立。
• 对异常值敏感，可能会影响模型的准确性。
• 无法捕捉特征之间的交互作用或非线性关系。

在实际应用中，线性模型通常作为基线模型，用于与其他更复杂的模型进行比较。如果数据集的特征和目标变量之间确实存在线性关系，线性模型可以提供非常有效的解决方案。