一.基本概念与实现
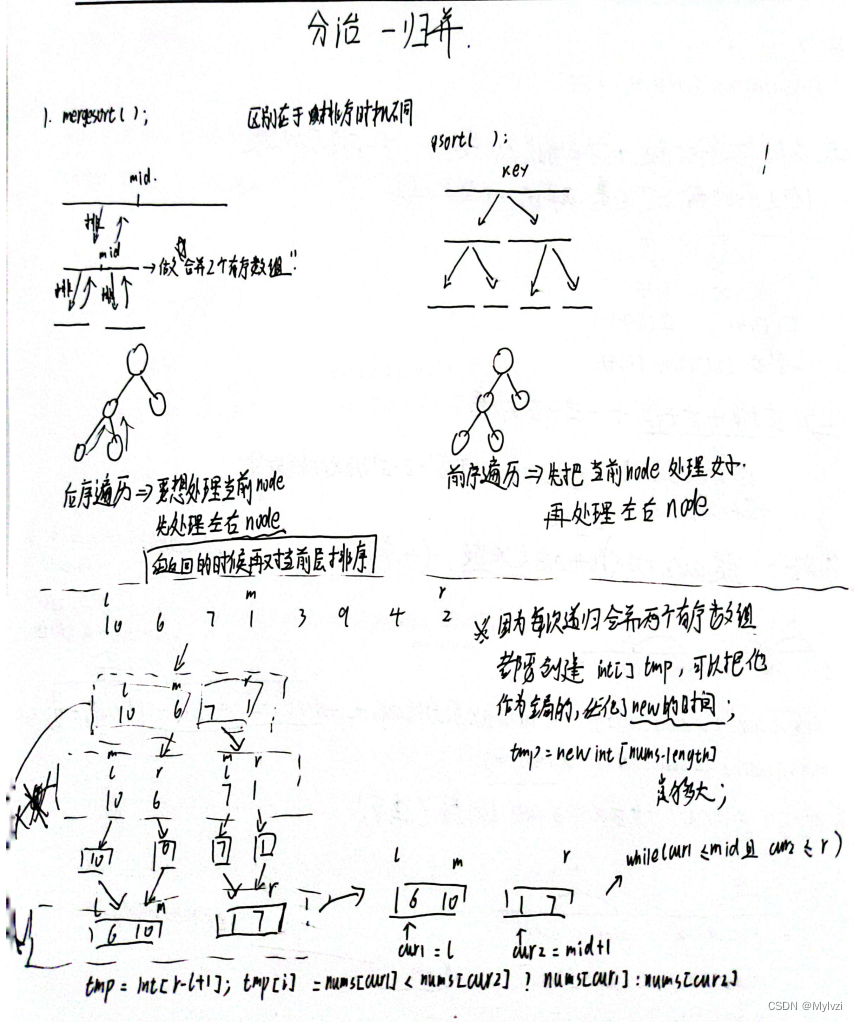
归并排序(mergeSort)也是基于分治思想的一种排序方式,思路如下:
- 分解:根据中间下标mid将数组分解为两部分
- 解决:不断执行上述分解过程,当分解到只有一个元素时,停止分解,此时就是有序的
- 合并:合并两个有序的子区间,所有子区间合并的结果就是原问题的解
归并排序和快速排序的区别在于排序的时机不同,归并排序是等到分解完毕之后在进行排序,快速排序是先进行分解,再排序;更形象的说,归并排序更像二叉树的后序遍历,遍历完左右子树再打印根节点;快速排序反之
代码:
class Solution {
int[] tmp;
public int[] sortArray(int[] nums) {
tmp = new int[nums.length];
mergeSort(nums, 0, nums.length - 1);
return nums;
}
private void mergeSort(int[] nums, int start, int end) {
if(start >= end) return;// 递归出口
int mid = (start + end) >> 1;
// 分解左右子树
mergeSort(nums, start, mid);
mergeSort(nums, mid + 1, end);
// 合并两个有序序列
merge(nums, start, mid, end);
}
private void merge(int[] nums, int l, int mid, int r) {
// 合并两个有序列表
int i = 0, i1 = l, i2 = mid + 1;
while(i1 <= mid && i2 <= r)
tmp[i++] = nums[i1] < nums[i2] ? nums[i1++] : nums[i2++];
while(i1 <= mid) tmp[i++] = nums[i1++];
while(i2 <= r) tmp[i++] = nums[i2++];
// 重新赋值
for(int j = l; j <= r; j++) nums[j] = tmp[j - l];
}
}
- 将tmp设置为全局减少每次
合并两个有序列表都要new所消耗的时间
2.利用归并排序求解逆序对
逆序对
链接:https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/description/

分析
-
最容易想到的思路就是
暴力解法,每遍历到一个数字就统计后面有多少个小于当前数字的数字,只要小于就满足逆序对的条件,时间复杂度为O(N^2),显而易见这种做法的时间复杂度过高,无法通过所有样例 -
可以这么想,每遍历到一个数字,我就想"如果我知道我前面有多少个比我大的数字该多好",就不需要再去一个一个遍历了,或者是每遍历到一个数字,“如果我知道后面有多少个比我小的数字该多好”
-
但是实际上不容易解决,不容易统计,比如
9,7,8这样的一个序列,你无法通过记录最值的方式统计有多少个大的数字,这是行不通的,好像唯一的解法就是从开头一直遍历到当前数字?可这就是暴力解法啊,如果能对前面的区间进行排序,得到大于当前数字的所有数字中的最小值,就能根据下标快速得到有多少个比我大的数字.那难道每遍历到一个数字就对前面的区间排一下序再找最小值吗?时间复杂度好像更高了,且不稳定 -
但是这个想法是好的,在遍历的过程中如果前面的元素是
有序的,那么就能降低时间复杂度,关于逆序对的求解,排序是一个很好的思路 -
排序一般都是
从小到大排序,无论哪种排序方式,对于一个乱序的数组,如果想让他变成有序的,就必须要进行元素的移动,就会将较小的数字放到较大的数字之前,可见排序就是消除逆序对的过程,以下是几种基于排序的求解逆序对的方法
01.冒泡排序
- 对于冒泡排序,每次元素交换就可以看做一次消除逆序对;使用全局变量ret记录元素交换的次数
- 冒泡排序的本质是"每次移动,都通过元素比较和元素交换让当前区间的最大值移动到区间末尾"
代码:
class Solution {
// 冒泡排序法
int ret;
public int reversePairs(int[] nums) {
bubbleSort(nums);
return ret;
}
private void bubbleSort(int[] nums) {
int n = nums.length;
for (int i = 0; i < n; i++) {
boolean flg = false;
for (int j = 0; j < n - 1 - i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums, j, j + 1);
flg = true;
}
}
if (!flg)
return;
}
}
private void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
++ret;
}
}
- 时间复杂度:
O(N^2)
02.插入排序
- 对于插入排序,每次元素的移动都可以看做一次
消除逆序对,使用一个全局变量ret记录元素移动的次数即可,时间比冒泡排序略快 - 插入排序就像是
往你的已有的有序的扑克牌中插入一个新牌,每次都是从后往前进行比较,进行插入
代码:
class Solution {
// 插入排序法
int ret;
public int reversePairs(int[] nums) {
for(int i = 1; i < nums.length; i++) {
int tmp = nums[i], j = i - 1;
while(j >= 0) {
if(nums[j] > tmp) {
nums[j + 1] = nums[j];
++ret;
}
else break;
--j;
}
nums[j + 1] = tmp;
}
return ret;
}
}
- 时间复杂度:
O(N^2)
03.归并排序(最快的解法)
代码:
class Solution {
int[] tmp;// 用于合并两个有序数组的临时数组
int ret;// 记录递归过程中的逆序对的个数
public int reversePairs(int[] nums) {
tmp = new int[nums.length];
mergeSort(nums, 0, nums.length - 1);// 归并排序
return ret;
}
private void mergeSort(int[] nums, int start, int end) {
if(start >= end) return;
int mid = (start + end) >> 1;
mergeSort(nums, start, mid);
mergeSort(nums, mid + 1, end);
merge(nums, start, mid, end);
}
private void merge(int[] nums, int l, int mid, int r) {
// 在合并的过程中统计逆序对的个数
// 关键步骤 合并两个有序数组
// 在合并的过程中统计逆序对的个数!!!
// 此处采用 的逻辑是:固定cur2,找cur1中比当前cur2大的数
// 在排序的过程中应该使用升序排序
int i = 0, i1 = l, i2 = mid + 1;
while(i1 <= mid && i2 <= r) {
if(nums[i1] > nums[i2]) {// 如果大 则i1后面的数字都比当前数字大 都能构成逆序对
ret += mid - i1 + 1;
tmp[i++] = nums[i2++];
}else {
tmp[i++] = nums[i1++];
}
}
while(i1 <= mid) tmp[i++] = nums[i1++];
while(i2 <= r) tmp[i++] = nums[i2++];
for(int j = l; j <= r; j++) nums[j] = tmp[j - l];
}
}
- 时间复杂度:
O(N*logN)
图解:


3.计算右侧小于当前数的个数
链接:https://leetcode.cn/problems/count-of-smaller-numbers-after-self/description/
分析
- 是上一题
逆序对的拓展版本 - 利用上面快速求解逆序对的思想,能够快速得到小于当前数字的数字的个数,需要注意的是,在归并排序的过程中原数组的元素会发生移动,但是只有归并完整个数组才能得到最终的结果,这个过程中我们要将数组元素和数组下标进行绑定,可以考虑使用index数组
- 当元素发生移动时,下标也跟着移动;
代码:
class Solution {
int[] tmpNum;
int[] tmpIndex;
int[] index;
int[] cnt;
public List<Integer> countSmaller(int[] nums) {
int n = nums.length;
tmpNum = new int[n];
tmpIndex = new int[n];
index = new int[n];
cnt = new int[n];
for(int i = 0; i < n; i++) index[i] = i;// 绑定索引
mergeSort(nums, 0, n - 1);
List<Integer> ret = new ArrayList<>();
for(int x : cnt) ret.add(x);
return ret;
}
private void mergeSort(int[] nums, int start, int end) {
if(start >= end) return;
int mid = (start + end) >> 1;
mergeSort(nums, start, mid);
mergeSort(nums, mid + 1, end);
merge(nums, start, mid, end);
}
private void merge(int[] nums, int l, int mid, int r) {
// 合并两个有序列表(降序排序)
// 可以快速得到有多少个数字小于当前数字
int i = 0, i1 = l, i2 = mid + 1;
while(i1 <= mid && i2 <= r) {
if(nums[i1] > nums[i2]) {
cnt[index[i1]] += r - i2 + 1;
tmpIndex[i] = index[i1];
tmpNum[i++] = nums[i1++];
}else {
tmpIndex[i] = index[i2];
tmpNum[i++] = nums[i2++];
}
}
// 处理未解决的元素
while(i1 <= mid) {
tmpIndex[i] = index[i1];
tmpNum[i++] = nums[i1++];
}
while(i2 <= r) {
tmpIndex[i] = index[i2];
tmpNum[i++] = nums[i2++];
}
// 重新赋值 原数组和下标数组都要更改
for(int j = l; j <= r; j++) {
nums[j] = tmpNum[j - l];
index[j] = tmpIndex[j - l];
}
}
}
4.反转对的个数
链接:
代码:
class Solution {
int[] tmp;
int ret;
public int reversePairs(int[] nums) {
int n = nums.length;
tmp = new int[n];
mergeSort(nums, 0, n - 1);
return ret;
}
private void mergeSort(int[] nums, int start, int end) {
if(start >= end) return;
int mid = (start + end) >> 1;
mergeSort(nums, start, mid);
mergeSort(nums, mid + 1, end);
merge(nums, start, mid, end);
}
private void merge(int[] nums, int l, int mid, int r) {
// 先统计当前有多少个翻转对
int i = 0, i1 = l, i2 = mid + 1;
while(i1 <= mid) {
while(i2 <= r && nums[i2] >= nums[i1] / 2.0) i2++;// 注意此处的除法需要存在小数位
if(i2 > r) break;
ret += r - i2 + 1;
i1++;
}
i1 = l; i2 = mid + 1;
while(i1 <= mid && i2 <= r) {
if(nums[i1] > nums[i2]) tmp[i++] = nums[i1++];
else tmp[i++] = nums[i2++];
}
while(i1 <= mid) tmp[i++] = nums[i1++];
while(i2 <= r) tmp[i++] = nums[i2++];
for(int j = l; j <= r; j++) nums[j] = tmp[j - l];
}
}
注意:
- 使用除法进行判断是为了防止越界
- /2和/2.0的结果是不同的
- 本题在合并两个有序列表之前需要先统计翻转对的个数,具体做法就是
暴力遍历两个数组,不能在合并的时候统计翻转对的个数