1. 对于JCA中基于密码的DES加密实现，固定一些盐和迭代计数，并记录加密/解密所需的平均时间;
2. 估计成功进行蛮力搜索攻击所需的时间

Name: NIHAO DONG

Number: 201476606

1. Password List:

N	Password
1	P@$$W0rD
2	thisismypassword
3	VeryLongP@$$W0rD

1. fix some salt and iteration count and record an average time required for encryption/decryption:

Salt：

Iteration count:

encryption/decryption code:

Record an average time required for encryption/decryption, Timestamps are used in JAVA to record the average time of five times.

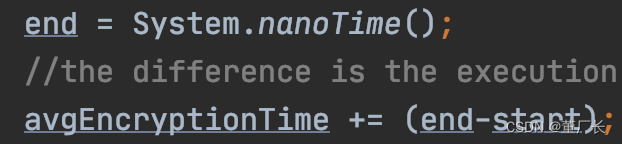
N	Password	Time for encryption/decryption
1	P@$$W0rD
2	thisismypassword
3	VeryLongP@$$W0rD

Based on the experimental results, we can see that the more complex the password, the longer it takes to encrypt/decrypt.

Delfs Hans(2015) explained this reason in his book "Introduction to Cryptography: Principles and Applications". He briefly described the PBE principle as follows: Password + Salt and then get the key through iteration, and then use the key to encrypt the plaintext through the symmetric algorithm. The more iterations there are, the more complex keys the encryption gets and the more time it takes. Similarly, the longer the decryption time is. But at the same time, the book also makes a comparison between ordinary computers and quantum computers, whose computer performance is the most important factor affecting time.

In conjunction with Paar Christof and Pelzl Jan (2010), an introduction to the importance of CPU performance in the prologue to “Understanding Cryptography: A Textbook for Students and Lens”. Through the comparison between ordinary computer and quantum computer, the conclusion is drawn that the speed of encryption and decryption depends on the performance of the computer under the same encryption algorithm.

1. Estimate the time required for successful brute-force search attack, assuming that an attacker knows:

Invariants : •the predefined plaintext;

•the ciphertext produced;

•the salt;

•the iteration count;

Variable: •but no password.

N	Password	Estimated time	The online server gives the time
1	P@$$W0rD	194years	8 hours
2	thisismypassword	2.35*10^8years	34 thousand years
3	VeryLongP@$$W0rD	5.119*10^20years	1 trillion years

A formula to calculate: S = x^L （Delfs Hans 2015）

1. S is the total number of possible digits

2. X is the number of possible values for each location in the password

3. L is the length of the password.

It takes about 0.0017 milliseconds to compute a hash (Mouha Nicky ie.2018). 1.7*10^-6 seconds in scientific notation.

Password "P @ $$W0rD". This password consists of four parts: Numbers, uppercase letters, lowercase letters, symbols. The number of character sets is (10+26+26+32) =94. Therefore, cracking the code takes on average (1.7*10^-6*96^8) s/2, which is about 70,970 days, or about 194 years.

Password "thisismypassword". This password consists of only lowercase letters. So there are 26 characters. The number of character sets is 26. Therefore, cracking this password takes on average (1.7*10^-6*26^16) s/2, about 7.413*10^16 seconds, or 857870370370 days, or about 2.35*10^8 years.

Password "VeryLongP @ $$W0rD". This password consists of four parts: Numbers, uppercase letters, lowercase letters, symbols. The number of character sets is (10+26+26+32) =94. Therefore, cracking this password takes on average (1.7*10^-6*96^16) /2, which is about 4.42*10^25, which is about 511921296296296300,000 days, which is about 5.119*10^20 years.

Combined with experimental results and literature. It concluded that the more complex the password, the longer it took brute force search to crack it.

1. Investigate how the time required for the attack depends on the iteration count:

Let's start with password No.3. (VeryLongP@$$W0rD)

Invariants:	password	plaintext	salt	ciphertext
Variable:	Iteration count

Here we set the time precision to MS to get the time needed for decryption.

Iteration count:	1000	100000	1000000	10000000
encryption Time:

After four experiments. When other conditions remain unchanged, the number of iterations keeps increasing. The encryption and decryption time required also increases.

At the same time, as an attacker, the attack process is as follows: brute search password, get the key through salt and iteration times, encrypt plaintext, get ciphertext. Verify that the password is correct against the ciphertext. (Regalado Daniel 2015) This means that total time = brute force search time + validation time.

Number of iterations: A single round does not provide sufficient security; Based on the paper "Finding Bugs in Cryptographic Hash Function Implementations" published by Mouha Nicky et al. (2018), and combined with the experimental results, it is obtained that: Cryptographic hash functions are security-critical algorithms with many practical applications, especially in digital signatures. The more complex the number of iterations, the more complex the key obtained.

1. Consider a variant of the attack, in which an attacker knows everything as above, except the iteration count, and estimate the time required to recover the passwords.

Invariants:	password	plaintext	salt	ciphertext
Variable:	Iteration count

Start with password No.2. (thisismypassword)

Iteration count:	1000	100000	1000000	10000000
Recover Time:

The results show that: The more iterations, The longer it takes to recover The password.

So the attacker already knows plaintext, ciphertext, salt. But we don't know the number of iterations. So if an attacker wants to recover the password, he doesn't need a reverse hash algorithm. The attacker just needs to collide and find a hash with the same password as the original value. As encryption is a hashing based on nonlinear functions, there is no decryption method. (Ferguson Niels 2010) This means that to retrieve the password corresponding to a hash, there is no choice but to try all possible passwords!

The following is summarized in Regalado Daniel's(2015) book "Ray Hat Hacking: The Ethical Hacker's Handbook" and Stallings William's article "Cryptography and Network Security: Principles and Practice". In theory, it is impossible to output the password backwards, because the information is lost in the encryption. It is impossible for an attacker to know which is the original plaintext. Given the limit of password length, there is likely to be only one that satisfies the hash. Suppose the user uses a 256bit hash, evenly distributed, with a password composed of Numbers and letters (36 choices) with a length fixed at 16 bits. Probability of collision: 1 - (2^256)! / (2^256^36^26 * (2^256 - 36^26)!),  Theta is close to 0. So a single hash is almost irreversible, which means that if an attacker uses a brute force search or rainbow table.

In summary, The attacker's password recovery time = brute force search cracking password time + collision verification.

Iteration count:	1000	100000	1000000	10000000
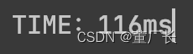
Attack Time:	2.35*10^8years +116ms	2.35*10^8years +220ms	2.35*10^8years +661ms	2.35*10^8years +4812ms

Based on the experimental results in Section 4, it is concluded that the number of iterations will affect the time of collision validation. Therefore, the number of iterations will have an impact on the attack time. The longer the number of iterations, the longer the attack takes.

1. Compare estimated time with the estimated time returned for the same passwords by online services and propose plausible explanation of any observed differences.

N	Password	Time on howsecureismypassword.net	Time on Kaspersky password checker	Estimated time
1	P@$$W0rD	8hours	2s	194years
2	thisismypassword	34 thousand years	This password appeared 3081 times in a database of leaked passwords.	2.35*10^8years
3	VeryLongP@$$W0rD	1 trillion years	15days	5.119*10^20years

Analysis of experimental results. Brute force searches take the longest, higher than online servers. But on an online server, the second site takes less time to return.

The reason is that the second online server has a database and can perform a "dictionary attack" (Wu Chwan-hwa 2013). The time complexity of this algorithm is a polynomial of the input scale, in this case the simplest unary equation, Y (algorithm running time) = X (the number of passwords in the data dictionary). So the dictionary attack time is much less than the brute force search time.

"Dictionary attacks are more effective than brute force searches" (Stallings, W. 2017), and Stallings makes a specific comparison in his book that brutal-force searches of the same complex password take much longer than dictionary attacks.

Brute force search is a simple and effective method of attack, but the time it takes depends on the complexity of the password and the performance of the computer.

(Estimated time compared to the first site, same as brute force search.) As an attacker, it can be improved, such as using dictionary attacks or rainbow tables to crack. More consideration should be given to the balance of space and time.

Reference:

• Yoon, J.W., Kim, H., Jo, H., Lee, H. & Lee, K. 2015, "Visual Honey Encryption: Application to Steganography", ACM, , pp. 65.

• Gomaa, I., Said, A.M., Abd-Elrahman, E., Hamdy, A. & Saad, E.M. 2017, "Performance Evaluation of Virtual Identity Approaches for Anonymous Communication in Distributed Environments", Procedia computer science, vol. 109, pp. 710-717.

• Paar, C. & Pelzl, J. 2010, Understanding cryptography: a textbook for students and practitioners, Springer, Heidelberg.

• Stallings, W. 2017, Cryptography and network security: principles and practice, 7th (global) edn, Pearson, Boston.

• Katz, J. 2010, Digital signatures, Springer, London;New York;.

• Delfs, H. & Knebl, H. 2015, Introduction to cryptography: principles and applications, 3rd edn, Springer, Heidelberg.

• Paar, C. & Pelzl, J. 2010, Understanding cryptography: a textbook for students and practitioners, Springer, Heidelberg.

• Mouha, N., Raunak, M.S., Kuhn, D.R. & Kacker, R. 2018, "Finding Bugs in Cryptographic Hash Function Implementations", IEEE transactions on reliability, vol. 67, no. 3, pp. 870-884.

• Regalado, D. 2015, Gray hat hacking: the ethical hacker's handbook, 4th edn, McGraw-Hill Osborne, New York.

• Thomas, T.M. & Stoddard, D. 2012, Network security first-step, 2nd edn, Cisco, Indianapolis, Ind.

• Wu, C. & Irwin, J.D. 2013, Introduction to computer networks and cybersecurity, CRC Press, Boca Raton.

• Ferguson, N. 2010, Cryptography engineering: design principles and practical applications, Wiley, Indianapolis, Ind.