贪心算法思路

以局部最优带动全局最优

LeetCode 455.分发饼干

题目详解

我做的是采用优先满足胃口的思路。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。这里是引用

从大到小进行遍历，所以一开始需要对两个数组进行遍历

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(s);
        Arrays.sort(g);
        int start=s.length-1;
        int count=0;
        for(int i= g.length-1;i>=0;i--)
        {
            if(start>=0 && g[i]<=s[start] )
            {
                
                start--;
                count++;
            }
        }
        return count;
    }
}

LeetCode 376. 摆动序列

题目详解

思路

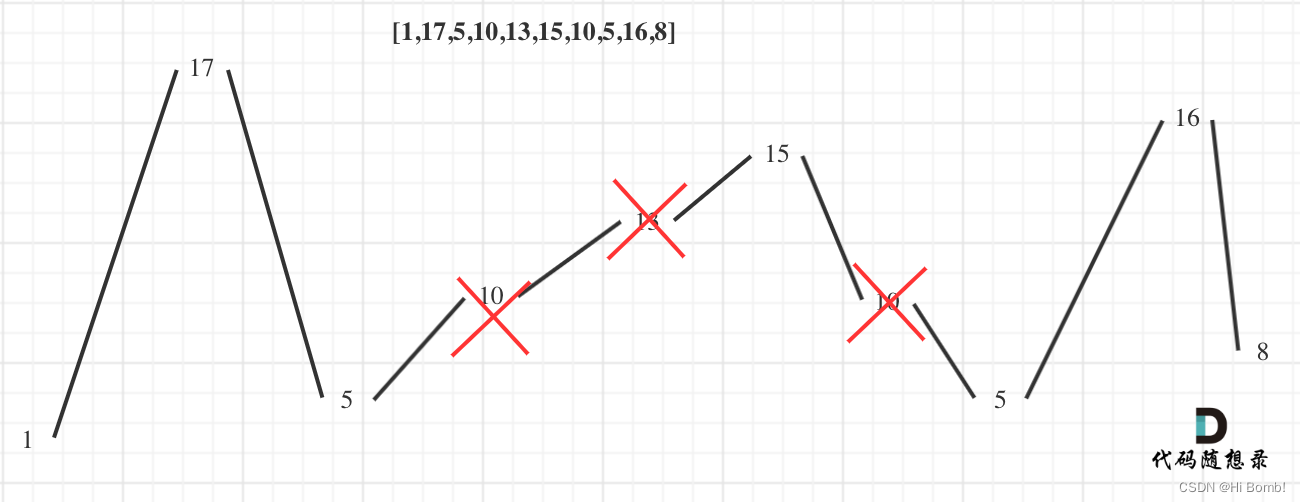
需要设定两个参数 CurDiff 和PreDiff 通过两个参数的差正负来判断是否是摆动序列

示图

在这里插入图片描述

class Solution {
    public int wiggleMaxLength(int[] nums) {
        if(nums.length<=1) return nums.length;
        int curDiff=0;
        int preDiff=0;
        int count=1;
        for(int i=1;i<nums.length;i++)
        {
            curDiff= nums[i]-nums[i-1];
            if((preDiff>=0&& curDiff<0)|| (preDiff<=0&& curDiff>0))
            {
                count++;
                preDiff= curDiff;
            }
        }
        return count;
    }
}

LeetCode 53. 最大子序和

题目详解

思路

局部最优是找到与和相比较更大的值如果 count 为负数就要重新计数

示图

在这里插入图片描述

class Solution {
    public int maxSubArray(int[] nums) {
       if(nums.length==1)
       { 
           return nums[0];
       }
        int sum=Integer.MIN_VALUE;
        int count=0;
        for(int i=0;i<nums.length;i++)
        {
            count +=nums[i];
            sum= Math.max( sum,count);
            if( count<=0)
            { 
                count=0;
            }
        }       
       return sum;
    }
}