数据结构实验二 :二叉树的操作与实现

news2025/4/6 4:41:24

数据结构实验一:线性表,堆栈和队列实现
数据结构实验二 :二叉树的操作与实现
数据结构实验三: 图的操作与实现
数据结构实验四 : 查找和排序算法实现

文章目录

  • 一、实验目的：
  • 二、使用仪器、器材
  • 三、实验内容及原理
    • 1、教材P247实验题1：实现二叉树的各种基本运算的算法
    • 2、教材P248实验题3：由遍历序列构造二叉树
    • 3、教材P248实验题5：构造哈夫曼树生成哈夫曼编码
    • 4、教材P248实验题8：简单算术表达式二叉树的构建和求值
    • 5、教材P249实验题9：用二叉树表示家谱关系并实现各种查找功能

一、实验目的：

1、领会二叉链存储结构和掌握二叉树中的各种基本运算算法设计；
2、领会线索二叉树的构造过程以及构造二叉树的算法设计；
3、领会哈夫曼树的构造过程以及哈夫曼编码的生成过程；
4、掌握二叉树遍历算法的应用，熟练使用先序、中序、后序3种递归遍历算法进行二叉树问题的求解；

二、使用仪器、器材

微机一台
操作系统：WinXP
编程软件：C/C++编程软件

三、实验内容及原理

1、教材P247实验题1：实现二叉树的各种基本运算的算法

编写一个程序btree.cpp，实现二叉树的基本运算，并在此基础上设计一个程序exp7-1.cpp完成以下功能。
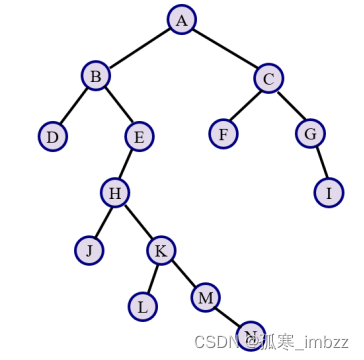
（1）由图7.33所示的二叉树创建对应的二叉链存储结构b，该二叉树的括号表示串为“A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,i)))”。
（2）输出二叉树b。
（3）输出‘H’结点的左、右孩子结点值。
（4）输出二叉树b的高度。
（5）释放二叉树b。

图7.33 一棵二叉树

#include<iostream>
using namespace std;
#include<stack>;

//（1）由图7.33所示的二叉树创建对应的二叉链存储结构b，该二叉树的括号表示串为“A(B(D, E(H(J, K(L, M(, N))))), C(F, G(, i)))”。
//（2）输出二叉树b。
//（3）输出‘H’结点的左、右孩子结点值。
//（4）输出二叉树b的高度。
//（5）释放二叉树b。

struct TreeNode {
	char data;
	TreeNode* left;
	TreeNode* right;
	TreeNode(char data) {
		this->data = data;
		this->left = NULL;
		this->right = NULL;
	}

};
/*
* 建树
*/
TreeNode* CreatTree(string TreeString, TreeNode*& root) {//建树
	const char* Tree = TreeString.c_str();
	stack<TreeNode*>temp;
	TreeNode* nodeTemp = NULL;
	bool flag = true;//左右孩子标记
	for (int i = 0; Tree[i] != '\0'; i++) {
		//遍历
		//如果是'('
		if (Tree[i] == '(') {
			//入栈 为下一个符号做准备
			temp.push(nodeTemp);//下面新建了节点
			flag = true;//flag == true 为下一个字符是左孩子
		}
		else if (Tree[i] == ',') {
			flag = false;//如果是 , 说明下一个字符是右孩子
		}
		else if (Tree[i] == ')') {
			temp.pop();//如果是')'  节点出栈舍弃 相当于指针向根部节点移动 
		}
		else {
			nodeTemp = new TreeNode(Tree[i]);//新建节点
			if (root == NULL) {//如果根节点为空 赋给根结点
				root = nodeTemp;
			}
			else {
				if (!temp.empty()) {//通过栈不空 说明还没有遍历完所以节点
					if (flag) {//建左点
						temp.top()->left = nodeTemp;
					}
					else {//建右点
						temp.top()->right = nodeTemp;
					}
				}
			}
		}
	}
	return root;
}

//遍历二叉树
void MidShow(TreeNode* root) {
	if (root == NULL) {
		return;
	}
	else {
		MidShow(root->left);
		cout << root->data;
		MidShow(root->right);
	}

}
//某个树的两个孩子
int showTwoKids(char S, TreeNode* root) {
	if (root->data == S) {//找到孩子 输出左右孩子
		if (root->left) {
			cout << "左孩子值:";
			cout << root->left->data;
		}
		else {
			cout << "左孩子空";
		}

		if (root->right) {
			cout << "右孩子值:";
			cout << root->right->data;
		}
		else {
			cout << "右孩子空";
		}
		return 1;
	}
	else {//没找到就前序遍历找
		showTwoKids(S, root->left);
		showTwoKids(S, root->right);
	}
	return 0;
}
//释放树
void deleteTree(TreeNode*& root) {

	if (root == NULL) {
		return;
	}
	else {
		deleteTree(root->left);
		deleteTree(root->right);
		cout << "删除:" << root->data << endl;
		delete root;
	}

}
/*
* 二叉树的高
*/
int showHigh(TreeNode* root) {
	if (root) {
		int m = showHigh(root->left);
		int n = showHigh(root->right);
		return m > n ? m + 1 : n + 1;
	}
}

int main() {
	string tree = "A(B(D(F,),E),C(,G))";
	TreeNode* root = NULL;
	CreatTree(tree, root);
	cout << endl;
	char findChar = 'A';
	cout << "A的左右孩子"<<endl;
	showTwoKids(findChar, root);
	cout << endl;
	cout << "树高:" << showHigh(root) << endl;
	cout << "中序遍历" << endl;
	MidShow(root);
	cout << endl;
	deleteTree(root);
	return 0;

2、教材P248实验题3：由遍历序列构造二叉树

编写一个程序exp7-3.cpp，实现由先序序列和中序序列以及由中序序列和后序序列构造一棵二叉树的功能（二叉树种的每个结点值为单个字符），要求以括号表示和凹入表示法输出该二叉树，并用先序遍历序列“ABDEHJKLMNCFGI”和中序遍历序列“DBJHLKMNEAFCGI”以及由中序遍历序列“DBJHLKMNEAFCGI”和后序遍历序列“DJLNMKHEBFIGCA”进行验证。

#include<iostream>
using namespace std;

struct TreeNode {
	char Data;
	TreeNode* l;
	TreeNode* r;
	TreeNode(char data) {
		this->Data = data;
		this->l = NULL;
		this->r = NULL;
	}
};
//前序和中序构造二叉树
TreeNode* CreatTreePre(string pre,string ins,TreeNode*&root) {
	int index = 0;
	TreeNode* p = root;
	if (pre.length() == 0 || ins.length() == 0) {
		return NULL;
	}
	else {
		//先序取根
		root = new TreeNode(pre[0]); //前序//A BDEHJKLMN CFGI //左右子树连续排列在一起
		                             //中序//D BJHLKMNE A FCGI//
		//中序找根
		while (ins[index] != root->Data) {
			index++;
		 }
		//递归建立左节点
		string leftins(ins, 0, index);
		string leftPre(pre, 1, index);
		//递归建立右节点
		string rightins(ins, index + 1, ins.length());
		string rightPre(pre,index+1,pre.length());
		root->l = CreatTreePre(leftPre, leftins, root->l);
		root->r = CreatTreePre(rightPre, rightins, root->r);
		//递归
	}
	return root;
}
//后序和中序构造二叉树
TreeNode* initTbyInPost(string postorder, string inorder) {
	if (postorder.length() == 0) return NULL;//没有节点
	TreeNode* node = new TreeNode(postorder[postorder.length() - 1]); //后续遍历的最后一个值是自身节点的值
	if (postorder.length() == 1) return node; //只有头节点
	int mid = inorder.find(postorder[postorder.length() - 1]);//当下节点
	string inorderLeft = inorder.substr(0, mid);//中序左节点
	string inorderRight = inorder.substr(mid + 1);//中序右节点
	string preordeLeft = postorder.substr(0, inorderLeft.length());//后序左节点
	string preordeRight = postorder.substr(inorderLeft.length(), inorderRight.length());//后序右节点
	node->l = initTbyInPost(preordeLeft, inorderLeft);
	node->r = initTbyInPost(preordeRight, inorderRight);
	return node;
}
//括号表示法
string bracketsShowTree(TreeNode* node) {
	if (!node)  return ""; //节点为空直接放回
	string s = string(1, node->Data);
	if (!node->l && !node->r) return s; //无子节点直接放回当下节点
	s.append("(");
	//括号内为当下节点的子节点
	s.append(bracketsShowTree(node->l));
	if (node->r) {
		//利用逗号隔开左右节点
		s.append(",");
		s.append(bracketsShowTree(node->r));
	}
	s.append(")");
	return s;
}
//中序遍历
void showTreePre(TreeNode*root) {
	if (root == NULL) {
		return;
	}
	else {
		showTreePre(root->l);
		cout << root->Data;
		showTreePre(root->r);
	}

}
//凹入法表示二叉树
void ConcavityShowTree(TreeNode*root,int i =0) {
	if (root) {
		cout << string(i * 3, ' ') << root->Data << endl;
		ConcavityShowTree(root->l, i + 1);
		ConcavityShowTree(root->r, i + 1);
	}
}
int main() {
	TreeNode* root1;
	TreeNode* root2;
	string pre = "ABDEHJKLMNCFGI";
	string ins = "DBJHLKMNEAFCGI";
	string tail ="DJLNMKHEBFIGCA";
	root1= CreatTreePre(pre, ins,root1);//造树
	root2= initTbyInPost(tail, ins);
	string s = "";
	//前序和中序
	cout << bracketsShowTree(root1)<<endl;
	//后序和中序
	cout << bracketsShowTree(root1)<<endl;
	//
	ConcavityShowTree(root1);

	return 0;
}

3、教材P248实验题5：构造哈夫曼树生成哈夫曼编码

编写一个程序exp7-5.cpp，构造一棵哈夫曼树，输出对应的哈夫曼编码和平均查找长度，并对下表（表7.8）所示的数据进行验证。

表7.8 单词及出现的频度
单词 The of a to and in that he is at on for His are be
频度 1192 677 541 518 462 450 242 195 190 181 174 157 138 124 123

#include<iostream>
#include<iomanip>
using namespace std;

/*
* tree
*/
struct TreeNode {
	int data;
	TreeNode* left;
	TreeNode* right;
	TreeNode(int data) {
		this->data = data;
		this->left = NULL;
		this->right = NULL;
	}
	TreeNode(int data, TreeNode* left, TreeNode* right) {
		this->data = data;
		this->left = left;
		this->right = right;
	}
};

//1.所有的叶子节点都必须是数字。
//2.所有的非叶子节点都是符号，而且都必须有左子树和右子树。
//3.不可能会存在一个节点仅存在左子树而不存在右子树，或者仅存在右子树而不存在左子树的情况。
//4.+ -节点只存在于最左边，左孩子只能是 + -或者数字，右孩子只能是 * / 或者数字
//5.* / 节点的右孩子只能是数字，左孩子只能是 * / 或者数字

/*
* 字符变数字
*/
int StringToInt(string val) {
	reverse(val.begin(), val.end());//反转
	int ans = 0;
	for (int i = 0; i < val.size(); i++) {//转数字
		ans += (val[i] - '0') * pow(10, i);
	}
	return ans;
}

/*字符串种树
* 1.所有的叶子节点都必须是数字。
 2.所有的非叶子节点都是符号，而且都必须有左子树和右子树。
//3.不可能会存在一个节点仅存在左子树而不存在右子树，或者仅存在右子树而不存在左子树的情况。
//4.+ -节点只存在于最左边，左孩子只能是 + -或者数字，右孩子只能是 * / 或者数字
//5.* / 节点的右孩子只能是数字，左孩子只能是 * / 或者数字
*/
TreeNode* creatTree(string s) {
	//s为空 返回null 
	if (s == "") {
		return NULL;
	}
	//从右往左遍历先找+-
	//for(int a =s.size()-1;a>=0&& s[a] != '+' && s[a] != '-';a--){}
	int i = s.size() - 1;
	while (i >= 0 && s[i] != '+' && s[i] != '-') {
		i--;//有可能是-1
	}
	if (i >= 0) {
		TreeNode* root = new TreeNode((int)s[i]);//char的形式转化为int
		root->left = creatTree(s.substr(0, i));
		root->right = creatTree(s.substr(i + 1));
		return root;
	}

	//找不到+/ 找*/
	// 新建节点 
	// 左指针指向 符号左边字符串
	// 右指针指向 符号右边字符串
	int j = s.size() - 1;
	while (j >= 0 && s[j] != '*' && s[j] != '/') {
		j--;
	}
	if (j >= 0) {
		TreeNode* root = new TreeNode((int)s[j]);//char的形式转化为int
		root->left = creatTree(s.substr(0, j));
		root->right = creatTree(s.substr(j + 1));
		return root;
	}
	//只有一个字符的时候才有会出现数字
	TreeNode* root = new TreeNode(StringToInt(s));
	return root;
}

/*
* calculater
*/
int calculate(TreeNode*root) {
	//只有符号才有左右子树
	if (!root) {//空返回0
		return 0;
	}
	//非空
	   //有左右子树 就是符号
	int res = 0;
	if (root->left && root->right) {
		switch (root->data) {
		case '+':
			res = calculate(root->left) + calculate(root->right);
			break;
		case'-':
			res = calculate(root->left) - calculate(root->right);
			break;
		case'*':
			res = calculate(root->left) * calculate(root->right);
			break;
		case'/':
			res = calculate(root->left) * calculate(root->right);
			break;
		}
	}
	else {//符号之外就是数字
		res = root->data;
	}
	return res;
	
}

void Delete(TreeNode*root) {
	if (root == NULL) {//空返回
		return;
	}
	else {
		Delete(root->left);
		Delete(root->right);
		root->left = NULL;
		root->right = NULL;
		delete root;
	}

}
int main() {
	string Test = "1+2*3-4/5";
	TreeNode* root=NULL;
	int sum;
	root= creatTree(Test);
	sum = calculate(root);
	cout << "1+2*3-4/5 ="<< endl;
	cout<<sum;
	Delete(root);
}

4、教材P248实验题8：简单算术表达式二叉树的构建和求值

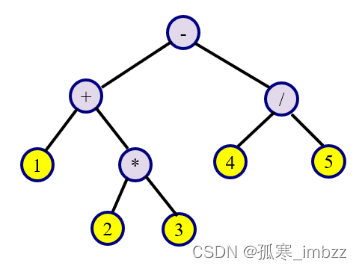
编写一个程序exp7-8.cpp，先用二叉树来表示一个简单算术表达式，树的每一个结点包括一个运算符或运算数。在简单算术表达式中只包含+、-、、/和一位正整数且格式正确（不包括括号），并且要按照先乘除后加减的原则构造二叉树，图7.34所示为“1+23-4/5”代数表达式对应的二叉树，然后由对应的二叉树计算该表达式的值。
在这里插入图片描述

#include<iostream>
#include<iomanip>
using namespace std;

/*
* tree
*/
struct TreeNode {
	int data;
	TreeNode* left;
	TreeNode* right;
	TreeNode(int data) {
		this->data = data;
		this->left = NULL;
		this->right = NULL;
	}
	TreeNode(int data, TreeNode* left, TreeNode* right) {
		this->data = data;
		this->left = left;
		this->right = right;
	}
};

//1.所有的叶子节点都必须是数字。
//2.所有的非叶子节点都是符号，而且都必须有左子树和右子树。
//3.不可能会存在一个节点仅存在左子树而不存在右子树，或者仅存在右子树而不存在左子树的情况。
//4.+ -节点只存在于最左边，左孩子只能是 + -或者数字，右孩子只能是 * / 或者数字
//5.* / 节点的右孩子只能是数字，左孩子只能是 * / 或者数字

/*
* 字符变数字
*/
int StringToInt(string val) {
	reverse(val.begin(), val.end());//反转
	int ans = 0;
	for (int i = 0; i < val.size(); i++) {//转数字
		ans += (val[i] - '0') * pow(10, i);
	}
	return ans;
}

/*字符串种树
* 1.所有的叶子节点都必须是数字。
 2.所有的非叶子节点都是符号，而且都必须有左子树和右子树。
//3.不可能会存在一个节点仅存在左子树而不存在右子树，或者仅存在右子树而不存在左子树的情况。
//4.+ -节点只存在于最左边，左孩子只能是 + -或者数字，右孩子只能是 * / 或者数字
//5.* / 节点的右孩子只能是数字，左孩子只能是 * / 或者数字
*/
TreeNode* creatTree(string s) {
	//s为空 返回null 
	if (s == "") {
		return NULL;
	}
	//从右往左遍历先找+-
	//for(int a =s.size()-1;a>=0&& s[a] != '+' && s[a] != '-';a--){}
	int i = s.size() - 1;
	while (i >= 0 && s[i] != '+' && s[i] != '-') {
		i--;//有可能是-1
	}
	if (i >= 0) {
		TreeNode* root = new TreeNode((int)s[i]);//char的形式转化为int
		root->left = creatTree(s.substr(0, i));
		root->right = creatTree(s.substr(i + 1));
		return root;
	}

	//找不到+/ 找*/
	// 新建节点 
	// 左指针指向 符号左边字符串
	// 右指针指向 符号右边字符串
	int j = s.size() - 1;
	while (j >= 0 && s[j] != '*' && s[j] != '/') {
		j--;
	}
	if (j >= 0) {
		TreeNode* root = new TreeNode((int)s[j]);//char的形式转化为int
		root->left = creatTree(s.substr(0, j));
		root->right = creatTree(s.substr(j + 1));
		return root;
	}
	//只有一个字符的时候才有会出现数字
	TreeNode* root = new TreeNode(StringToInt(s));
	return root;
}

/*
* calculater
*/
int calculate(TreeNode*root) {
	//只有符号才有左右子树
	if (!root) {//空返回0
		return 0;
	}
	//非空
	   //有左右子树 就是符号
	int res = 0;
	if (root->left && root->right) {
		switch (root->data) {
		case '+':
			res = calculate(root->left) + calculate(root->right);
			break;
		case'-':
			res = calculate(root->left) - calculate(root->right);
			break;
		case'*':
			res = calculate(root->left) * calculate(root->right);
			break;
		case'/':
			res = calculate(root->left) * calculate(root->right);
			break;
		}
	}
	else {//符号之外就是数字
		res = root->data;
	}
	return res;
	
}

void Delete(TreeNode*root) {
	if (root == NULL) {//空返回
		return;
	}
	else {
		Delete(root->left);
		Delete(root->right);
		root->left = NULL;
		root->right = NULL;
		delete root;
	}

}
int main() {
	string Test = "1+2*3-4/5";
	TreeNode* root=NULL;
	int sum;
	root= creatTree(Test);
	sum = calculate(root);
	cout << "1+2*3-4/5 ="<< endl;
	cout<<sum;
	Delete(root);
}

5、教材P249实验题9：用二叉树表示家谱关系并实现各种查找功能

编写一个程序exp7-9.cpp，采用一棵二叉树表示一个家谱关系（由若干家谱记录构成，每个家谱记录由父亲、母亲和儿子的姓名构成，其中姓名是关键字），要求程序具有以下功能。
文件操作功能：家谱记录的输入，家谱记录的输出，清除全部文件记录和将家谱记录存盘。要求在输入家谱记录时按从祖先到子孙的顺序输入，第一个家谱记录的父亲域为所有人的祖先。
家谱操作功能：用括号表示法输出家谱二叉树，查找某人的所有儿子，查找某人的所有祖先（这里的祖先是指所设计的二叉树结构中某结点的所有祖先结点）。

#include <iostream>
#include<string>
#include<fstream>
using namespace std;
typedef long long ll;

typedef struct Node {
	string name; //姓名
	Node* left;  //左指针
	Node* right;  //右指针
	Node* parent;  //双亲
	bool isBoy;  //1男 0女
	Node() {
		name = "";
		left = NULL;
		right = NULL;
		parent = NULL;
		isBoy = 1;
	}
}TreeNode;
Node* root = NULL;
ifstream ifs;
ofstream ofs;
string level, f, m;

//根据文件内容建树
void init(TreeNode*& t, int depth = 1) {

	//默认祖先一定存在
	//如果丈夫没有妻子就没有孩子
	//一次读入三种字符 同一层级别标准 父亲名字 母亲名字
	t = new TreeNode();
	t->name = f;
	TreeNode* wife = 0;
	if (m != ".") {//如果没有老婆用 '.'表示
		//有妻子
		wife = new TreeNode();
		wife->name = m;
		wife->isBoy = 0;
		wife->parent = t;
		t->left = wife;
	}
	level = "";

	ifs >> level >> f >> m;	//继续读入3个数据
	if (ifs.eof()) {   //如果读完了，就直接返回
		return;
	}
	if (level.size() == depth) { //辈分一样，说明是兄弟
		init(t->right, depth);  //递归建树
		t->right->parent = t;
	}
	else if (level.size() == depth + 1 && wife) {//层数符号是当前的下一层 老婆存在 说明有儿子 
		//建立儿子
		init(wife->right, depth + 1);
		wife->right->parent = wife;
	}
	else {
		//如果都不是，那么返回去给上一层
		return;
	}

	//上面递归return后的还剩下的a b c继续判断 
	if (level.size() == depth) {
		init(t->right, depth);
		t->right->parent = t;
	}

}

//括号法输出二叉树
void bracketingPrint(TreeNode* t = root) {
	if (!t) {
		return;
	}
	cout << t->name;
	if (t->left || t->right) {
		cout << "(";
		bracketingPrint(t->left);
		if (t->right) {
			cout << ",";
			bracketingPrint(t->right);
		}
		else {
			cout << ",";
		}
		cout << ")";
	}
}

//根据名称寻找
TreeNode* findPeople(string name, TreeNode* t = root) {
	if (!t) {
		return 0;
	}
	if (t->name == name) {
		return t;
	}
	TreeNode* n = findPeople(name, t->left);
	if (n) {
		return n;	//如果在左边找到就返回左边的
	}
	return findPeople(name, t->right);	//否则返回右边的
}

//查找某人的所有儿子
void findAllChildren(string name) {
	cout << "---------------------------------------" << endl;
	cout << "找 " << name << " 所有儿子 " << endl;
	TreeNode* node = findPeople(name);
	if (!node) {
		cout << "查不到" << name << endl;   //找不到这个人
		return;
	}
	if (node->isBoy) {
		//如果是男的
		if (!(node->left)) {
			cout << name << " 没有妻子!" << endl;   //他没有妻子
			return;
		}
		node = node->left;
	}
	//女的
	if (node->right) {
		node = node->right;
		cout << name << "所有的儿子 " << " 在此:" << endl;
		while (node) {
			cout << node->name << endl;
			node = node->right;
		}
	}
	else {
		//没有儿子
		cout << name << " 没有儿子!" << endl;
	}
}

void findAllAncestors(string name) {
	cout << "----------------------------------------" << endl;
	cout << "找" << name << "所有祖先" << endl;
	TreeNode* node = findPeople(name);
	if (!node) {
		cout << "People " << name << " 没有找到!!!" << endl;   //找不到这个人
		return;
	}
	if (!node->isBoy) {
		//女，与祖先们不构成血缘关系，忽略
		cout << name << " 不是男性!!!" << endl;
		return;
	}
	cout << "所有的祖先 " << name << " 在此:" << endl;
	node = node->parent;
	while (node) {
		if (node->isBoy) {
			cout << node->name << endl;
			node = node->parent;
			cout << node->name << endl;
		}
		node = node->parent;   //一直往上寻找
	}
}

/*
输出家谱
*/
void printGenealogy(TreeNode* t = root, int depth = 0) {
	if (!t) {
		return;
	}
	cout << string(depth + 1, '#') << " " << t->name << " ";
	if (t->left) {
		cout << t->left->name << endl;
		printGenealogy(t->left->right, depth + 1);
	}
	else {
		cout << "." << endl;
	}
	printGenealogy(t->right, depth);
}
/*
输出家谱到文件
*/
void printGenealogyToFile(TreeNode* t = root, int depth = 0) {
	if (!t || !ofs.is_open()) {
		return;
	}
	ofs << string(depth + 1, '#') << " " << t->name << " ";
	if (t->left) {
		ofs << t->left->name << endl;
		printGenealogyToFile(t->left->right, depth + 1);
	}
	else {
		ofs << "." << endl;
	}
	printGenealogyToFile(t->right, depth);
}

/*
销毁二叉树
*/
void destory(TreeNode* node = root) {
	if (node == NULL) {
		return;  //已经为NULL，无需销毁
	}
	destory(node->left);
	destory(node->right);
	node->left = NULL; //销毁之后需要把指针置空
	node->right = NULL;
	delete node;
}

void showOutTree(Node* root, int i = 0) {
	if (root) {
		cout << string(i * 3, ' ') << root->name << endl;
		showOutTree(root->left, i + 1);
		showOutTree(root->right, i + 1);
	}
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	ifs.open("Z:\\mdzz.txt", ios::in); //打开data.txt文件
	if (!ifs.is_open()) {
		cout << "打开失败";
		return 0;
	}
	ifs >> level >> f >> m;    //读入文件里面的3个数据
	init(root);			//递归建树
	showOutTree(root);
	ifs.close();   //使用完成后要关闭流
	bracketingPrint();   //括号法输出
	cout << endl;
	findAllChildren("s1");   //查找zhangsan的所有儿子
	findAllChildren("f3");   //查找lujiajing的所有儿子
	findAllChildren("f4");   //查找所有儿子
	findAllChildren("f5");   //查找所有儿子
	findAllAncestors("f6");   //查找他的所有祖先
	findAllAncestors("f8");   //查找他的所有祖先
	cout << "输入到文件" << endl; // 输出家谱
	printGenealogy();
	//输出家谱到文件
	ofs.open("Z:\\mdzz.txt", ios::out);
	cout << "以上为输入文件内容" << endl; // 输出家谱到文件
	printGenealogyToFile();
	destory();  //销毁二叉树
	root = 0;   //置空
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/190118.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Mybatis 笔记

Mybatis 笔记

一、mybatis简介 1.1 框架概念 软件的半成品&#xff0c;完成软件开发过程中的通用操作&#xff0c;实现特定的功能&#xff0c;从而简化开发人员在软件开发中的步骤&#xff0c;提升开发效率。 1.2 常用框架 MVC框架&#xff1a;简化servlet的开发步骤&#xff0c;与前端交…
阅读更多...
java实现oracle和mysql的group by分组功能|同时具备max()/min()/sum()/case when 函数等功能

java实现oracle和mysql的group by分组功能|同时具备max()/min()/sum()/case when 函数等功能

一、前言oracle和mysql的group by 分组功能大家应该清楚&#xff0c;那如何使用java实现同样的功能呢比如下面这个表idnameagemathEnglish10yujianlin2092.5103ww84102520102611036310351020我们需要按id分组&#xff0c;求最大age和math累计成绩我们的sql应该这样写select id,…
阅读更多...
Linux下的安装环境

Linux下的安装环境

目录 软件安装常识 Linux软件安装生态 Linux软件生态的本土化 yum的三板斧&#xff1a;查找、安装、卸载 yum补充的3个小知识 软件安装常识 我们知道Linux下有一条命令可以下载安装指令&#xff0c;那就是yum。在了解yum之前得先说一下Linux的整体安装环境。 Linux下用y…
阅读更多...
每日学术速递2.1

每日学术速递2.1

CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.Cv 1.SeaFormer: Squeeze-enhanced Axial Transformer for Mobile Semantic Segmentation 标题&#xff1a;SeaFormer:用于移动语义分割的挤压增强型轴向变换器 作者&#xff1a; Qian…
阅读更多...
从 await-to-js 到 try-run-js

从 await-to-js 到 try-run-js

之前在做 code review 时候发现有同事使用 try catch 包装了一堆异步代码&#xff0c;于是个人就觉得很奇怪&#xff0c;难道不应该只 catch 可能出问题的代码吗&#xff1f;同事告诉我说 try catch 太细的话会出现内外作用域不一致&#xff0c;需要提前声明变量。 let res: D…
阅读更多...
【微服务】微服务保护Sentinel

【微服务】微服务保护Sentinel

微服务保护Sentinel1.初识Sentinel1.1.雪崩问题及解决方案1.1.1.雪崩问题1.1.2.超时处理1.1.3.仓壁模式1.1.4.断路器1.1.5.限流1.1.6.总结1.2.服务保护技术对比1.3.Sentinel介绍和安装1.3.1.初识Sentinel1.3.2.安装Sentinel1.4.微服务整合Sentinel2.流量控制2.1.簇点链路2.1.快…
阅读更多...
豆瓣引流流程

豆瓣引流流程

豆瓣引流注册账号养号如何把豆瓣的帖子打造好并且引流到微信注册账号 第一&#xff1a;可以去营业厅或者卡商那里购买一批卡来进行注册。 第二&#xff1a;可以通过接码平台进行大量的一个小号注册&#xff0c;我们注册的号前期是作为一个顶帖号来使用。 第三&#xff1a;我…
阅读更多...
商业智能 BI 跟业务系统的思维差异

商业智能 BI 跟业务系统的思维差异

我们在跟企业的沟通过程中经常发现&#xff0c;很多企业还是分不清商业智能 BI 跟一般的业务信息化系统定位、用户、思维层面上的差异。因为在企业的IT信息化规划中&#xff0c;基础的业务系统建设一定是走在前面的&#xff0c;有了这些系统基础&#xff0c;才会有数据的积累&a…
阅读更多...
Python绘制图片一

Python绘制图片一

文章目录一、代码段讲解1. theta np.linspace(0.0, 2 * np.pi, N , endpointFalse)2. ax plt.subplot(111,projectionpolar)3. bar.set_facecolor(plt.cm.viridis(r / 10.))4. bar.set_alpha(0.5)二、附录一、代码段讲解 1. theta np.linspace(0.0, 2 * np.pi, N , endpoint…
阅读更多...
Windows软件：如何使用VMware® Workstation 16 Pro安装Centos7操作系统

Windows软件：如何使用VMware® Workstation 16 Pro安装Centos7操作系统

前言&#xff1a; 在我们开发Java项目当中&#xff0c;经常会将jar包部署在Linux操作系统中运行&#xff0c;其中Centos7使用最广泛&#xff0c;前后端的各种运行环境所必须的软件均在此上运行&#xff0c;本章我们就来讲一下如何使用VMware安装Centos7系统&#xff0c;以便我们…
阅读更多...
08技术太卷我学APEX-页面上显示静态图片

08技术太卷我学APEX-页面上显示静态图片

08技术太卷我学APEX-页面上显示静态图片 0 我想在首页面上留个人微信二维码和微信群二维码 我想在《技术太卷我学APEX》首页上留下联系方式&#xff0c;方便同学们加群一起交流联系方式。 先手机登录个人微信&#xff0c;截图个人微信二维码和《技术太卷我学APEX》微信群二维…
阅读更多...
【MyBatis持久层框架】MyBatis参数传递详细解读

【MyBatis持久层框架】MyBatis参数传递详细解读

文章目录1. 前言2. MyBatis 参数传递3. 多个参数4. 单个参数4.1 POJO类4.2 Map集合类4.3 Collection集合类型4.4 List集合类型4.5 Array类型4.6 其他类型5. 总结1. 前言 前面在使用配置文件实现增删改查一文中&#xff0c;我们说到&#xff0c;使用 MyBatis 的 Mapper 代理开发…
阅读更多...
glibc memcpy内部机制学习记录

glibc memcpy内部机制学习记录

判断需要拷贝的字节数是否大于临界值&#xff08;16或8&#xff09;。如果小于&#xff0c;直接按照one byte by one byte来拷贝。如果大于&#xff1a; 1、先进行内存对齐。假设要拷贝的目的地址如下所示 其中start为拷贝目的地的起始地址 &#xff0c;end为拷贝目的地的结束…
阅读更多...
企业的内部文档太杂乱，有什么好用的文档管理软件？

企业的内部文档太杂乱，有什么好用的文档管理软件？

企业内部文档的管理&#xff0c;是一个老生常谈的问题。 有些企业的文档管理比较混乱&#xff0c;很难做好企业内部的信息管控。 我们可以先从以下几个方面入手&#xff1a; 企业内部文档杂乱分散&#xff0c;集中式的管理&#xff1b;信息更新不及时、错误频繁&#xff0c;通过…
阅读更多...
大数据NiFi（十六）：处理器Connection连接

大数据NiFi（十六）：处理器Connection连接

文章目录 处理器Connection连接 一、查看队列中的FlowFile 二、查看FlowFile自定义属性值
阅读更多...
【数据结构初阶】第一节.初识时间和空间复杂度

【数据结构初阶】第一节.初识时间和空间复杂度

文章目录 前言 一、认识数据结构 二、时间复杂度 2.1 时间复杂度的概念 2.2 计算时间复杂度 2.2.1 大O的渐进表示法 2.3 常见时间复杂度计算举例 三、空间复杂度 3.1 空间复杂度的概念 3.2 计算空间复杂度 3.3 常见空间复杂度计算举例 四、常见复杂度的对比&#xff1…
阅读更多...
CVE-2022-26937 Windows NFS 栈溢出漏洞分析

CVE-2022-26937 Windows NFS 栈溢出漏洞分析

简介 NFS全称Network File System&#xff0c;即网络文件系统&#xff0c;用于服务器和客户机之间文件访问和共享的通信&#xff0c;从而使客户机远程访问保存在存储设备上的数据。 CVE-2022-26937是微软5月份修复的Windows NFS中一个对NLM响应处理不当的栈溢出漏洞&#xff…
阅读更多...
OAuth2（1）

OAuth2（1）

目录 一、什么是OAuth2.0 二、OAuth2中的角色 三、认证流程 四、生活中的OAuth2思维 五、令牌的特点 六、OAuth2授权方式 1.授权码 2.隐藏方式 3.密码方式 4.凭证方式 一、什么是OAuth2.0 OAuth2.0是目前使用非常广泛的授权机制&#xff0c;用户授权第三方应用…
阅读更多...
红宝书学习

红宝书学习

第一章 认识js js的组成部分有哪些&#xff1f; ①ecma 核心语法 api ②dom 提供与网页内容交互的方法和接口 ③bom 浏览器对象模型&#xff0c;提供了和浏览器交互的接口 use strict 是什么&#xff1f; use strict 是一种 ECMAscript5 添加的&#xff08;严格模式&#xff…
阅读更多...
玩了半年NFT，一心进军Web3的Prada到底要怎么玩？

玩了半年NFT，一心进军Web3的Prada到底要怎么玩？

图片来源&#xff1a;无界AI绘画工具生成2022年1月&#xff0c;奢侈品品牌Prada与阿迪达斯玩了一把“联合营销”&#xff0c;玩法是这样的&#xff1a;首先&#xff0c;两个品牌邀请粉丝上传个人照片&#xff0c;然后&#xff0c;品牌抽取3000名粉丝的作品&#xff0c;交由数字…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023