目录
- 一、简介
- 二、易错点
- 三、例子
- 四、万能模板
- 五、参考资料
一、简介
哪怕没有学过编程的同学,也许不知道二分法这个名字,但也一定接触过它的核心思想。不了解的同学也没关系,我用一句话就能概括出它的精髓:将一个区间一分为二,每次都舍弃其中的一部分。
二分法能够极大地降低我们在解决问题时的时间复杂度。假如你要在一个单调递增的数组a[n]中寻找一个数target,遍历的话时间复杂度是O(n)。但如果采用二分法,时间复杂度则是O(log n)。这种效率的提高无疑是巨大的!
二、易错点
1、while循环中是写 left < right 还是写 left <= right ?
2、如下图所示,if(nums[mid]>target),右边界更新区间时是写成 right = mid 还是 right = mid-1?

这两点是很容易弄混的。要弄清楚上面这两个问题的答案,首先要确定你想写的循环的区间到底是左闭右开还是左闭右闭?(题目没明确要求的话就看你个人选择,都是可以的)
左闭右闭的区间是这样写的:[left, right]
它包含了 left 和 right 这两个数
左闭右闭的区间是这样写的:[left, right)
它包含了 left,但不包含 right 。
假设我选择了左闭右闭,此时需要在数组nums中寻找一个数target,找到的话返回下标,没找到的话返回 -1,伪代码如下:
left=0;
right=nums.size()-1;
while(l <= r){ // 注意这里不是 l < r
int mid = l + (r - l)/2;
if(nums[mid] > target) right = mid-1;
else if(nums[mid] < target) left = mid+1;
else{
return mid;
}
}
首先,为什么选择左闭右闭的区间,第3行就要写成<=呢?因为写入while循环的判断条件应该与你选择的区间相吻合,而左闭右闭的区间包含了left和right,也就是说可能会出现 left== right的情况。如果写成<,那么就漏掉了left==right 这种情况,所以应该写成<=。
其次,第5行右边界为什么更新为 mid-1 而不是更新为 mid?因为我们已经确定了nums[mid] > target,所以mid一定不是我们要找的值,因此在下一轮搜索中,不应再包含mid这个数。而我们选择的是左闭右闭区间,它包含了左右边界,每次搜索时都会包含左右边界。所以为了使已经被排除的mid不被再次搜索,右边界应该更新为mid-1。
假设我选择了左闭右开,此时需要在数组nums中寻找一个数target,找到的话返回下标,没找到的话返回 -1,伪代码如下:
left=0;
right=nums.size();
while(l < r){ // 注意这里不是 l < r
int mid = l + (r - l)/2;
if(nums[mid] > target) right = mid;
else if(nums[mid] < target) left = mid+1;
else{
return mid;
}
}
return -1;
左闭右开代表包含左边界,不包含右边界。右边界一定比左边界大,不存在 right == left 的情况。所以第3行只能写成<。
而第5行之所以写成right=mid,是因为下一次搜索中本就不会包含right,我们也确定了right不是要找的值,所以直接写成right=mid就可以了。
此时,注意第2行,因为左闭右开不包含右边界,所以右边界要设置为nums.size(),这样才能把nums.size()-1包含在搜索区间里。
三、例子
如果你已经理解了上面的内容,可以尝试做下面这道题:
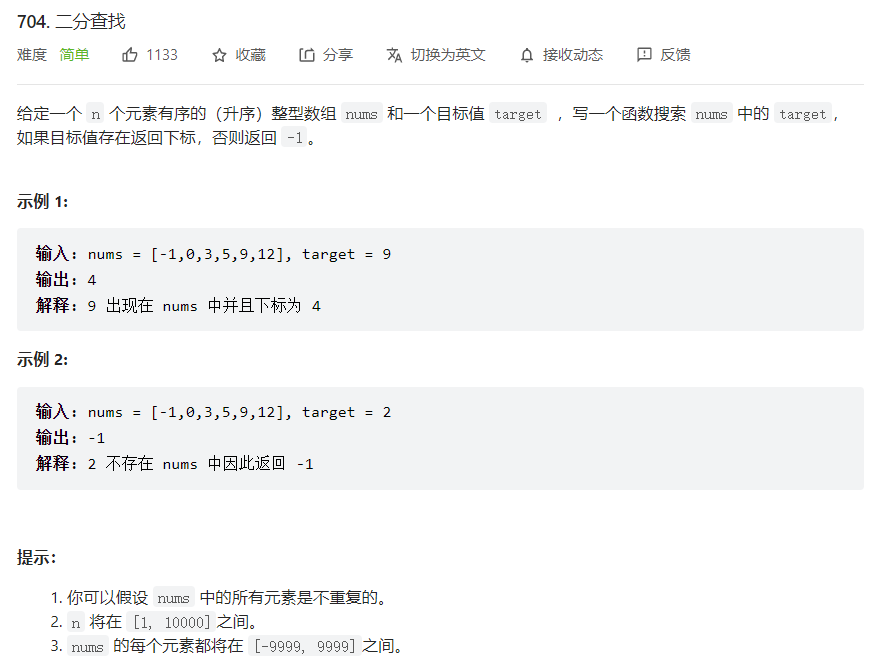
左闭右闭:
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while(l <= r){
int m = l + (r - l)/2;
if(nums[m] > target)r = --m;
else if(nums[m] < target) l = ++m;
else{
return m;
}
}
return -1;
}
};
左闭右开:
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0, r = nums.size();
while(l < r){
int m = l + (r - l)/2;
if(nums[m] > target)r = m;
else if(nums[m] < target) l = ++m;
else{
return m;
}
}
return -1;
}
};
四、万能模板
尽管理解了上面的内容,但很多时候解题还是会遇到困难。
比如说给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
你会发现上面的两个代码很难应用到这种题,所以我找到了一个万能模板,跟大家分享一下:
class Solution {
/**
* 如果返回值等于 nums.size(),代表 nums 中不存在 满足 nums[i] >= target 的 i,也就是所有元素都小于 target。
* 否则返回满足 nums[i] >= target 的最小 i(最左 i)。也就是说,如果有多个连续的 target,会返回最靠左的那个的下标。
* nums为单调不减数组
* target为边界值
**/
public: int binarySearch(vector<int>& nums, int target) {
int l = 0, r = nums.size()- 1; // 二分查找的左右初始边界
while(l <= r){ // 注意这里不是 l < r
int m = l + (r - l)/2;
if(nums[m] >= target)r = --m;
else l = ++m;
}
return l; // 此时,l 代表arr[i] >= x 的最小 i。
}
};
如何运用这个模板去解决不同的问题呢?请往下看
1、查找某个数 x 首次出现的位置,如果不存在,返回-1。
如果 binarySearch(arr, x) == nums.size(),代表所有元素都小于x,也就无法查找到 x 首次出现的位置;如果有多个元素等于 x,则 binarySearch(arr, x) 代表 x 首次出现的位置的下标;如果binarySearch(arr, x) != x,则不存在某个数等于 x,binarySearch(arr, x) 代表最靠左的大于 x 的数。
2、查找某个数 x 最后出现的位置,如果不存在,返回-1。
将该问题转换为用 int ret = binarySearch(arr, x+1) - 1 来解决。 如果ret < 0,返回 -1;否则,如果nums[ret] == x,ret 就是答案;否则,返回 -1。
3、查找某个数 x 首次出现的位置,如果不存在 x,则求出适合插入 x 的位置。
binarySearch(arr, x)就是。
4、查找小于x的最后一个数。
转换为用binarySearch(arr, x) - 1来解决,注意判断存在性。
5、查找小于x的第一个数。
这是个伪问题。
6、查找大于x的第一个的数。
转换为用binarySearch(arr, x + 1)来解决,注意判断存在性。
7、查找大于x的最后一个的数。
这是个伪问题。
举例:
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
-
1 <= nums.length <= 1 0 4 10^4 104
-
- 1 0 4 10^4 104 <= nums[i] <= 1 0 4 10^4 104
-
nums 为 无重复元素 的 升序 排列数组
-
- 1 0 4 10^4 104 <= target <= 1 0 4 10^4 104
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1; // 二分查找的左右初始边界
while(l <= r){ // 注意这里不是 l < r
int m = l + (r - l)/2;
if(nums[m] >= target)r = --m;
else l = ++m;
}
return l; // 此时,l 代表arr[i] >= tarhget的最小 i。
}
};
五、参考资料
1、二分查找万能模板
2、【二分查找】详细图解