文章目录

前言
一、复杂DP
- 例题
- - 例题1：AcWing 1050. 鸣人的影分身（线性dp）
  - - 分析
    - 题解：DP
  - 例题2：AcWing 1047. 糖果（背包问题变形）
  - - 分析
    - 题解：DP（01背包问题变形）
  - 例题3：AcWing 1222. 密码脱落（中等，区间DP，蓝桥杯）
  - - 分析
    - 题解：区间dp
  - 例题4：AcWing 1220. 生命之树（树型DP）
  - - 分析
    - 题解：树形DP
  - 例题5：AcWing 1303. 斐波那契前 n 项和（矩阵快速幂）
  - - 分析
    - 题解：矩阵快速幂
- 习题
- - 习题1：AcWing 1226. 包子凑数（最大公约数+完全背包）
  - - 分析
    - 题解：数论+完全背包DP变型（二维及一维解）二维
  - 习题2：AcWing 1070. 括号配对（中等，区间DP）
  - - 分析
    - 题解1：区间DP（DP状态表示最小值）
    - 题解2：区间DP（DP状态表示最大值）
  - 习题3：AcWing 1078. 旅游规划（树型DP）
  - - 分析
    - 题解：树型DP及树的直径
  - 习题4：AcWing 1217. 垒骰子（中等，蓝桥杯）
  - - 分析
    - 题解：线性DP，矩阵快速幂
参考文章

前言

前段时间为了在面试中能够应对一些算法题走上了刷题之路，大多数都是在力扣平台刷，目前是400+，再加上到了新学校之后，了解到学校也有组织蓝桥杯相关的程序竞赛，打算再次尝试一下，就想系统学习一下算法（再此之前是主后端工程为主，算法了解不多刷过一小段时间），前段时间也是第一次访问acwing这个平台，感觉上面课程也是比较系统，平台上题量也很多，就打算跟着acwing的课程来走一段路，大家一起共勉加油！

目前是打算参加Java组，所以所有的题解都是Java。

所有博客文件目录索引：博客目录索引(持续更新)

本章节复杂DP习题一览：包含所有题目的Java题解链接

第八讲学习周期：2023.1.27-2023.1.31

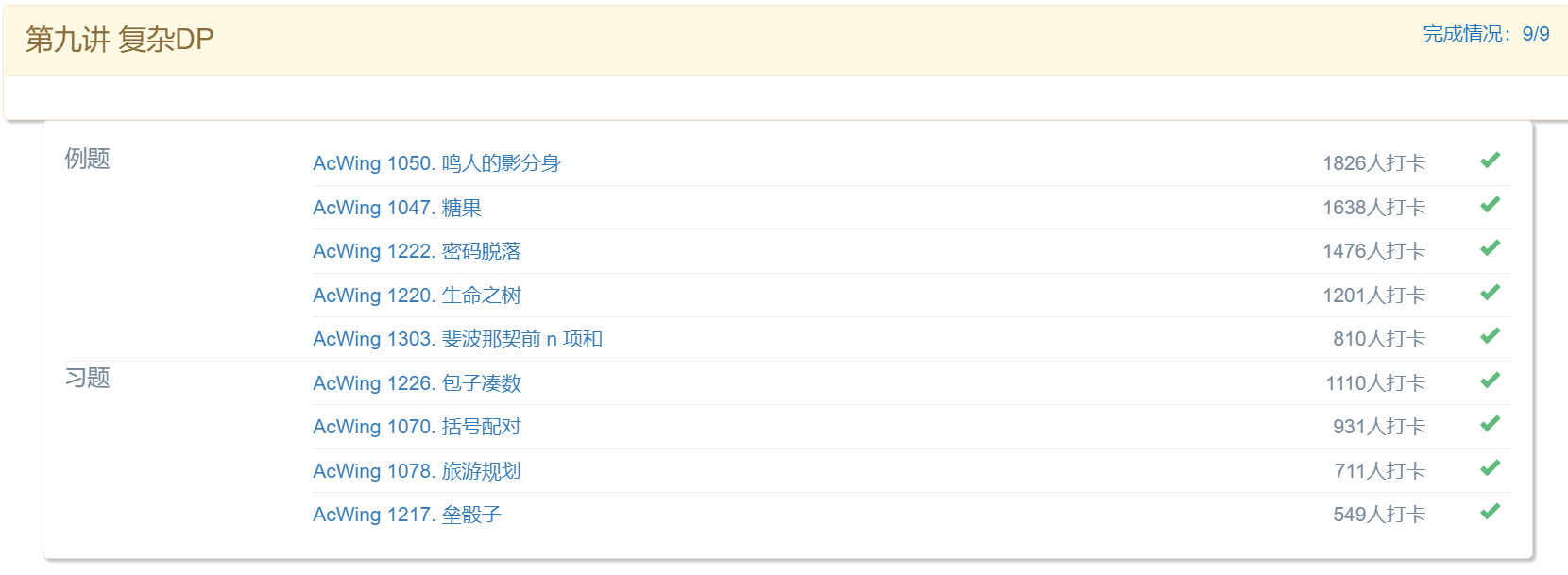
例题：

AcWing 1050. 复杂DP-例题鸣人的影分身（线性DP）
AcWing 1047. 复杂DP-例题糖果（背包问题变形，分析及Java题解）
AcWing 1222. 复杂DP-例题密码脱落（区间DP，分析及Java题解）
AcWing 1220. 复杂DP-例题生命之树（树型DP，详细分析及Java题解）
AcWing 1303. 复杂DP-例题斐波那契前 n 项和（矩阵快速幂，分析及Java题解）

习题：

AcWing 1226. 复杂DP-习题包子凑数（数论+完全背包，分析及Java题解）
AcWing 1070. 复杂DP-习题括号配对（区间DP，两种DP思路，分析及Java题解）
AcWing 1078. 复杂DP-习题旅游规划（树型DP，分析及Java题解）
AcWing 1217. 复杂DP-习题垒骰子（线性DP，矩阵快速幂，分析及Java题解）

一、复杂DP

例题

例题1：AcWing 1050. 鸣人的影分身（线性dp）

题目链接：AcWing 1050. 鸣人的影分身

分析

整数划分做法：m划分n个数，这n个数从大到小放置。

下面采用动态规划做法。

状态表示：f[i][j]

集合：总和为i，可以分为j个数的方案。
属性：方案的个数。

状态计算：根据当前方案中最小值是否为0

最小值为0：直接表示上一层方案(i不变，j-1)也就是f[i][j - 1]。
最小值不为0：说明都大于等于1，直接全部减去一，把上面所对应的状态拿过来加一就是这种状态f[i-j][j]。

题解：DP

复杂度分析：时间复杂度O(m.n)；空间复杂度O(m.n)

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static final int N = 11;
    static int[][] f = new int[N][N];
    static int t, m, n;
    
    public static void main(String[] args) {
        t = cin.nextInt();
        while (t-- != 0) {
            m = cin.nextInt();
            n = cin.nextInt();
            //初始化为1
            f[0][0] = 1;
            for (int i = 0; i <= m; i ++) {
                for (int j = 1; j <= n; j ++ ) {
                    //有0，直接f[i][j-1]把上一种情况直接拿过来
                    f[i][j] = f[i][j - 1];
                    //无0，直接将现有的加上i-j状态的即可
                    if (i >= j) f[i][j] += f[i - j][j];
                }
            }
            System.out.println(f[m][n]);
        }
    }
}

例题2：AcWing 1047. 糖果（背包问题变形）

题目链接：AcWing 1047. 糖果

分析

状态定义：dp(i, j)代表前i个物品价值%k=j的集合。

最终我们目标的是dp[n][0]，表示的是选购n个物品，且n个物品%k的值为0的最大值。

状态转移方程：dp(i, j) = max(dp(i - 1，j)，dp(i - 1, (j - w[i] % k)) + w[i])

我们期望的是选购i个商品时有最大值，理想的状态为：（S + w[i]）% k == 0，但是并不是选购的每一个都能够达到%k==0的情况，所以我们可以以%k的结果值j来作为限制，假设理想的状态为j，那么每次选购商品可以由j - w[i]来推算出上一次的最大满足值构成%k=j的情况，也就是dp(i - 1，j - w[i])。

注意：由于对应的j是从0开始枚举的，而由于每个商品的价值>0，此时我们要考虑j - w[i]为负数的情况！若是a - b < 0，那么可以((a - b) % k + k) % k即可。

题解：DP（01背包问题变形）

复杂度分析：时间复杂度O(n²)；空间复杂度O(n²)

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static final int N = 110;
    static int[] w = new int[N];
    static int[][] dp = new int[N][N];
    static int n, k;
    
    //防止a-b出现负数情况
    public static int mod_sub (int a, int b) {
        return ((a - b) % k + k ) % k;
    }
    
    public static void main(String[] args) {
        n = cin.nextInt();
        k = cin.nextInt();
        for (int i = 1; i <= n; i ++ ) {
            w[i] = cin.nextInt();
        }
        //初始化dp，默认都是最小值
        for (int i = 0; i < N; i ++ ) 
            for (int j = 0; j < N; j ++) dp[i][j] = Integer.MIN_VALUE;
        dp[0][0] = 0;
        //遍历所有产品
        for (int i = 1; i <= n ; i++ ) {
            //枚举所有目标%k的值,[0, k - 1]
            for (int j = 0; j < k; j ++ ) {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][mod_sub(j, w[i])] + w[i]);
            }
        }
        System.out.println(dp[n][0] == Integer.MIN_VALUE ? 0 : dp[n][0]);
    }
}

例题3：AcWing 1222. 密码脱落（中等，区间DP，蓝桥杯）

题目链接：AcWing 1222. 密码脱落

分析

题目要求：最少添加几个才能将给出的字符串变为一个回文字符串。

看下数据量，最大为1000，时间复杂度为O(n²)、O(n².logn)一般就是dp了。

发现规律：最少添加的数量实际上就是最少删除的数量。

举例：ABDCDCBABC，我们删除掉第三个以及最后两个就能够构成一个回文字符串。

实际上对应我们删掉的字符我们在构成回文字符串中间对应镜像另一边添加删去的那个字符也即可变为回文字符串。
添加过后的字符串为：BCABDCDCDBABC。

此时我们可以使用dp来求得最长回文串的长度，接着最终使用总长度-最长回文串长度即可。

至少脱落的种子数 = 总长度 — 最长回文串的长度。

看到一个题解画的动态规划图很好，我这边直接引用该篇博客文章的图不再重新画了：AcWing 1222. 密码脱落

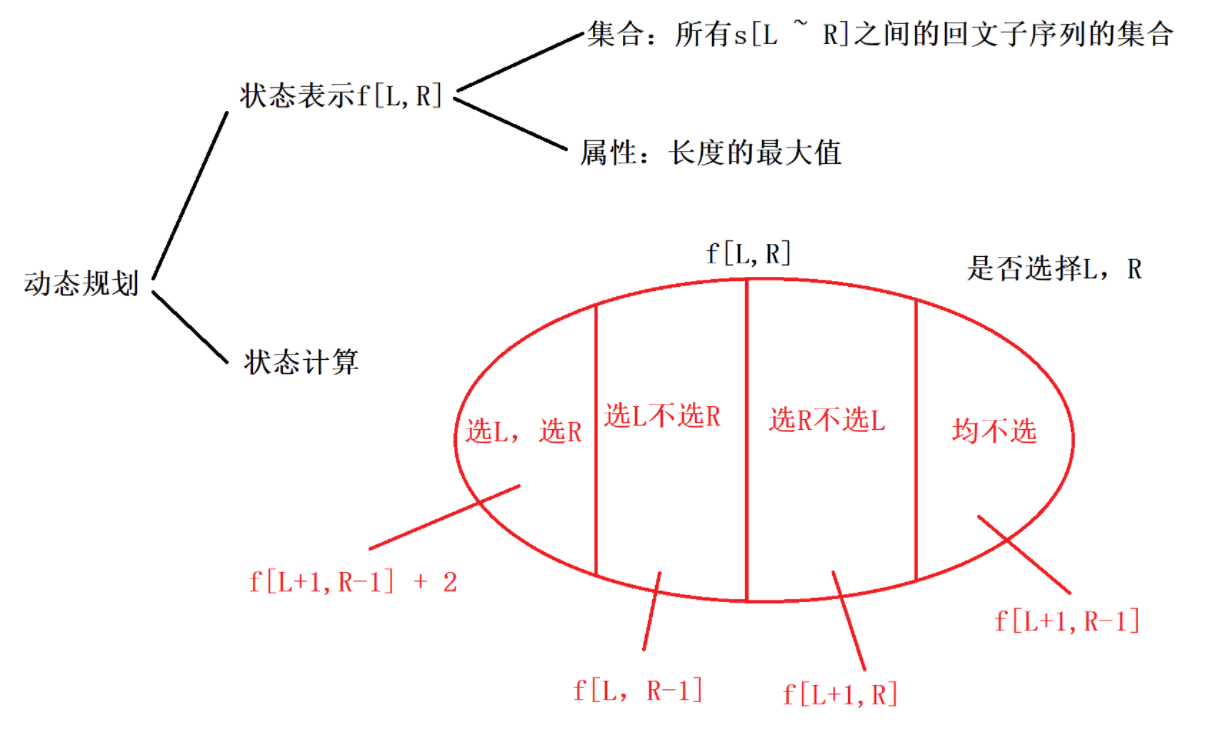
状态定义：dp(l，r)表示的是区间[l, r]中最长回文串的长度。

状态初始化：dp(l, r)本身单个字符时为1。

状态转移方程：

若是选择L与R位置的字符，则为f[L + 1, R + 1] + 2。
- 若是s[l] = s[r]，那么此时dp[l + 1][r - 1] + 2，就是区间[l + 1, r - 1]最大的回文串长度加上l、r位置两个字符数量。
若是区间[l + 1, r]回文串长度>区间[l, r]长度，那么此时dp[l][r] = dp[l + 1][r]
若是区间[l, r - 1]回文串长度>区间[l, r]长度，那么此时dp[l][r] = dp[l][r - 1]
若是区间[l + 1, r - 1]回文串长度 > 区间[l, r]长度，那么此时dp[l][r] = dp[l + 1][r - 1]。【注意，实际上对于dp[l + 1][r - 1]是被dp[l + 1][r]与dp[l][r - 1]覆盖的，所以这里可以进行省略】

实际举例：abba，最终构成的dp数组为

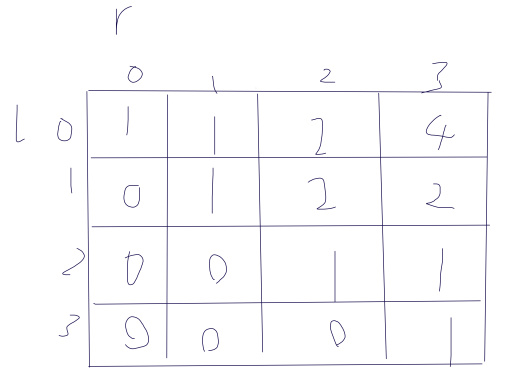
建议是根据dp走一遍画下图就能够很容易的理解了。

题解：区间dp

复杂度分析：时间复杂度O(n²)；空间复杂度O(n²)

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static final int N = 1010;
    static char[] arr;
    //dp[i][j]表示在[i, j]区间字符串中有最大的回文串长度
    static int[][] dp = new int[N][N];
    
    public static void main (String[] args) {
        arr = cin.next().toCharArray();
        int n = arr.length;
        //初始化
        for (int i = 0; i < n; i ++ ) dp[i][i] = 1;
        //转移方程
        for (int len = 1; len <= n; len ++ ) {
            //左区间
            for (int l = 0; l + len - 1 < n; l ++) {
                //右区间
                int r = l + len - 1;
                //防止越界
                if (len > 1) {
                    if (arr[l] == arr[r]) dp[l][r] = dp[l + 1][r - 1] + 2;
                    if (dp[l + 1][r] > dp[l][r]) dp[l][r] = dp[l + 1][r];
                    if (dp[l][r - 1] > dp[l][r]) dp[l][r] = dp[l][r - 1];   
                }
            }
        }
        //整个字符串最大的回文串长度为dp[0][n - 1]
        //求得我们要删去的字符数量则为n - dp[0][n - 1]
        System.out.println(n - dp[0][n - 1]);
    }
    
}

例题4：AcWing 1220. 生命之树（树型DP）

题目链接：AcWing 1220. 生命之树

分析

数据量为10万，时间复杂度一般为O(n.logn)，O(n)；

本题是采用树状DP来进行解决。图本身就是是一颗无向树，任意设置一个点为根，一定会存在一个和树根最近的一个点。

接着我们首先来拿示例作为举例：

5
1 -2 -3 4 5
4 2
3 1
1 2
2 5

第一行表示有5个节点，第二行表示1-5个节点的权重值，最后n-1行则是节点u到节点v。

采用树型DP做法是我们将各个给我们的u、v存储两次朝向，一次是u->v，另一个是v->u，将其存储在一个数组形式的邻接表中(单链表形式)。

实际分别存入边的顺序为：

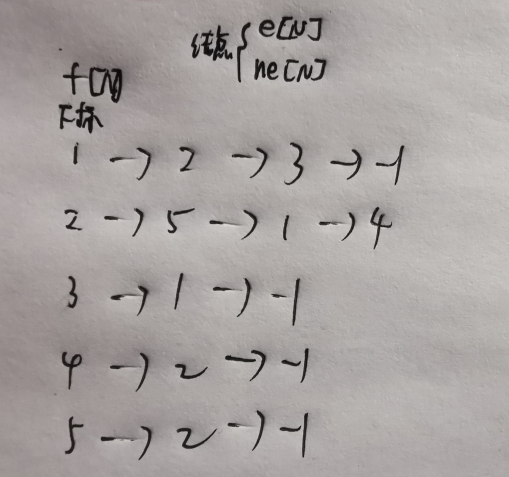
最终构成的一棵树如下：

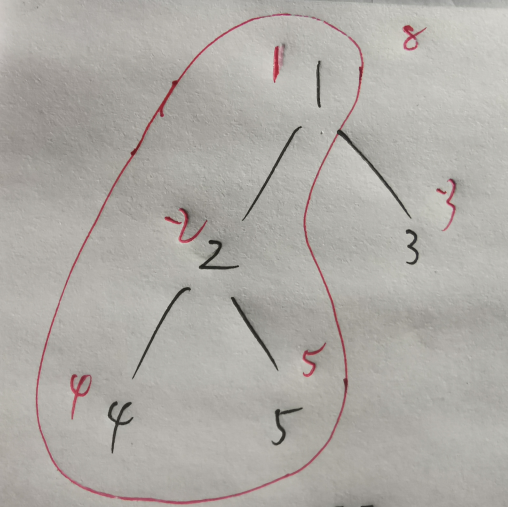
对于add()函数一开始直接蒙蔽，因为不知道其到底是怎么样的一个数据结构形式(我是直接看的acwing蓝桥杯，没有看基础班)，实际上这部分代码是图的一个邻接表代码实现使用单链表数组形式。

y总视频讲解：树、图邻接表数组实现：第三章搜索与图论（一）树和图的存储 01:16:00。

本题是直接使用dfs来求出包含某个节点子树最大权值和，对于子树权重若是<0我们则直接取0即可。

状态表示：f[i]。表示i节点子树的最大权值和。以节点i为根的子树中包含u的所有连通块最大值。

状态计算：f[i] = w[i] + ∑_i−>jmax(0, f[j])。

题解：树形DP

复杂度分析：时间复杂度O(n)；空间复杂度O(n)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    //双向邻接表开两倍
    static final int N = 200010;
    //无向图邻接表写法(数组链表形式)
    //e、ne表示一个节点的编号以及下一个节点的编号。h表示多个单链表头节点
    static int[] e = new int[N], ne = new int[N], h = new int[N];
    //存储节点权重，下标为编号，值为编号值
    static int[] w = new int[N];
    //对应根节点为i的最大评分
    static long[] f = new long[N];
    //n表示读入节点的数量，idx表示创建节点的下标
    static int n, idx;
    
    //添加一条边到对应h[a]开头的单链表中
    public static void add (int a, int b) {
        //采用头插法
        //创建第idx节点，设置第idx的编号以及下一个节点的编号
        e[idx] = b;
        ne[idx] = h[a];
        //更新该链表头节点的最新编号
        h[a] = idx++;
    }
    
    //dfs深搜图
    public static long dfs(int root, int father) {
        //初始化节点权重
        f[root] = w[root];
        for (int i = h[root]; i != -1; i = ne[i]) {
            int j = e[i];
            //若是当前节点是上一个节点直接跳过
            if (j == father) continue;
            //以j为根节点的都包含一个子树，我们只需要>0的权重值
            f[root] += Math.max(dfs(j, root), 0);
        }
        return f[root];
    }
    
    public static void main(String[] args) throws Exception{
        //初始话所有的头节点值为-1
        Arrays.fill(h, -1);
        n = Integer.parseInt(cin.readLine());
        String[] ss = cin.readLine().split(" ");
        //根据对应节点编号来进行初始化该节点的权重
        //i为节点编号，值为权重
        for (int i = 1; i <= n; i ++ ) {
            w[i] = Integer.parseInt(ss[i - 1]);
        }
        //读取所有的边（读取双向边）
        for (int i = 1; i < n; i ++ ) {
            ss = cin.readLine().split(" ");
            int a = Integer.parseInt(ss[0]);
            int b = Integer.parseInt(ss[1]);
            add(a, b);
            add(b, a);
        }
        
        //进行递归处理
        //任意一个根节点都可以作为出发路径，因为1个点能够去访问所有节点
        //这里默认是从节点1开始出发，父节点为-1
        dfs(1, -1);
        
        //遍历所有节点中的最大权重，找到最大的一个
        Long res = f[1];
        for (int i = 2; i <= n; i ++ ) {
            res = Math.max(res, f[i]);
        }
        System.out.println(res);
    }
}

例题5：AcWing 1303. 斐波那契前 n 项和（矩阵快速幂）

分析

本题n的长度到达了20亿，基本本题的时间复杂度应该是O(logn)

对于斐波那契额数列我们可以采用矩阵乘法来进行表示，左边矩阵中包含斐波那契的第n-1以及第n项[fn, fn-1] * 固定矩阵可以得到[fn+1, fn]。

举例：

[1, 0] * $\left[\begin {array}{c} 1 &1 \\ 1 &0 \end{array}\right]$ = [1, 1]。此时矩阵的第二个1表示f(1)

接着使用[1, 1] * $\left[\begin {array}{c} 1 &1 \\ 1 &0 \end{array}\right]$ = [2, 1]，假设[1, 0]为[fn, fn-1]

那么[fn, fn-1] * $\left[\begin {array}{c} 1 &1 \\ 1 &0 \end{array}\right]$ = [fn + 1, fn]

那么对于求得fn的值我们可以从[1, 0]开始，分别表示[f1, f0]，进行n次乘该固定矩阵即可求得[fn+1, fn]，此时矩阵的第二个元素就是我们要求的值。

此时我们要求指定的一个斐波那契数列的值fn，公式即为[f1, f0] * Aⁿ = [fn+1, fn]，右边Aⁿ一个常数矩阵的n次方，此时我们就可以使用矩阵快速幂来实现时间复杂度O(logn)的优化。

对于矩阵乘法以及矩阵快速幂的实现可见该博客：快速幂及矩阵快速幂分析及代码实现

又题目说让我们去求前n项的和，我们可以去进行找规律：

f1 = f3 - f2
f2 = f4 - f3
f3 = f5 - f4
...
fn = fn+2 - fn+1

我们进行相加最后可以发现为fn = fn+2 - f2 = fn+2 - 1，也就是说我们只需要求到fn+2即可ac该题

所以最终方案就是使用矩阵快速幂求得fn+2，接着减去1即可求得结果。

题解：矩阵快速幂

复杂度分析：时间复杂度O(logn)；空间复杂度O(1)

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static long n, m;
    //定义fn的初始矩阵
    static long[] fn = {1, 0};
    //乘法矩阵
    static long[][] a = {
        {1, 1},
        {1, 0}
    };
    
    //矩阵乘法  一维乘二维
    public static void multi (long[] a, long [][] b) {
        long[] ans = new long[2];
        for (int i = 0; i < 2; i ++ ) 
            for (int j = 0; j < 2; j ++ ) 
                ans[i] += a[j] * b[i][j] % m;
        //拷贝ans的值到a数组中
        for (int i = 0; i < 2; i ++ )
            a[i] = ans[i] % m;
    }
    
    //矩阵乘法 二维乘二维
    public static void _multi(long[][] a, long[][] b) {
        long[][] ans = new long[2][2];
        //矩阵乘法
        for (int i = 0; i < 2; i ++ ) 
            for (int j = 0; j < 2; j ++ ) 
                for (int k = 0; k < 2;k ++) 
                    ans[i][j] += a[i][k] * b[k][j] % m;
        //拷贝
        for (int i = 0; i < 2; i ++) 
            for (int j = 0; j < 2; j ++ )
                a[i][j] = ans[i][j] % m;
    }
    
    
    public static void main(String[] args) {
        n = cin.nextLong();
        m = cin.nextLong();
        
        //进行矩阵累乘n + 2次
        n += 2;
        while (n != 0) {
            if ((n & 1) == 1) multi(fn, a);
            _multi(a, a);
            n >>= 1;
        }
        System.out.println((fn[1] - 1 + m) % m);
    }
    
}

习题

习题1：AcWing 1226. 包子凑数（最大公约数+完全背包）

题目链接：AcWing 1226. 包子凑数

分析

本题是数论+完全背包问题。

题目问的是给你指定n笼装有不同数量的蒸笼，且你可以选择不限量的蒸笼个数，让你求得有多少个不能够组合的数的情况。

本题是完全背包的变形：有几个物品，每个物品有无限个，每个物品选任意个，能够组合到指定数量。

完全背包：每件物品有无限个(也就是可以放入背包多次），求怎样可以使背包物品价值总量最大。

解决问题1：通过什么来进行判定是否有无限个不能够组合成的数量？

对于是否能够组合成指定数量，我们可以借助裴蜀定理：若是a,b是整数，且gcd(a, b) = d，那么一定存在整数x,y，使ax+by=d成立。

博客：欧几里得与扩展欧几里得算法(含推导过程及代码)

也就是说任意两个重量的物品若是其公约数为1则能够凑到任意重量的数字(数额选择含负数)，若是不为1则会由无限个不能够组合的。

为什么不为1有无限个不能够组合的？

因为若是gcd(a, b)=2，那么其只能组合为2及2的倍数，其他数字如3、5、7这类必然不能组成到！

问题2：对于有限个组合数字数量如何确定？

若是两个是互质数，即gcd(a, b) = 1，那么a,b最大不能表示的数是：(a−1)(b−1)−1 = ab - a- b。如果不互质，那么不能表示的数有无穷多个。

本题中A最大值为100，那么最大的两个互质数为99、100，此时最大不能表示的数为ab - a- b = 9900-99-100=9701，我们本题可直接设置为上限10000。

接着对于不能够组成指定重量的数量我们来进行分析。

状态定义：dp(i, j)，前i个数量是否能够组成重量为j。

初始化：f[0][0] = true。前0个构成重量为0是可构成的。

状态转移方程：f[i][j] = f[i - 1][j] | f[i][j - A]

f(i, j) = f(i - 1, j) | f(i - 1, j - A) | f(i - 1, j - 2A) | ...
f(i, j - A) = f(i - 1, j - A) | f(i - 1, j - 2A) | f(i - 1, j - 3A) | ...
简化为：f[i][j] = f[i - 1][j] | f[i - 1][j - w[i]]

实际上可以使用一维数组来进行替代二维数组。

题解：数论+完全背包DP变型（二维及一维解）二维

时间复杂度O(n)，数量量上限为10000，N最大是100也就是100万。空间复杂度O(n²)

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static final int N = 110;
    static int n;
    //存储每种笼可放的个数
    static int[] w = new int[N];
    //转移方程
    static boolean[][] f = new boolean[N][N * N];
    
    public static int gcd(int a, int b) {
        if (b == 0) return a;
        return gcd(b, a % b);
    }
    
    public static void main(String[] args) {
        n = cin.nextInt();
        //读取值并求得gcd公约数
        int d = 0;
        for (int i = 1; i <= n; i ++ ) {
            w[i] = cin.nextInt();
            d = gcd(d, w[i]);
        }
        //若是w!=1则有无限多个组合数
        if (d != 1) {
            System.out.println("INF");
        }else {
            //初始化方程
            f[0][0] = true;
            //动态规划
            //i表示选择前i个笼类型
            for (int i = 1; i <= n; i ++) {
                //j表示前i个笼能够组合的目标重量
                for (int j = 0; j <= 10000; j ++) {
                    //若是i-1件可以组合，那必然也能够组合
                    f[i][j] = f[i - 1][j];
                    //若是当前目标重量>=第i个笼的数量，来进行转移方程，这里要使用|，因为若是f[i][j]本身可以组成，碰到f[i][j - w[i]
                    //为false也不会变为false
                    if (j >= w[i]) f[i][j] |= f[i][j - w[i]];
                }
            }
            int ans = 0;
            //去遍历所有能够构成的目标值j，若是为false表示不能够组成
            for (int j = 0; j <= 10000; j ++) 
                if (!f[n][j]) ans++;
            System.out.println(ans);
        }
    }
    
}

实际上我们可以将dp转为1维：

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static final int N = 110;
    static int n;
    //存储每种笼可放的个数
    static int[] w = new int[N];
    //转一维
    static boolean[] f = new boolean[N * N];
    
    public static int gcd(int a, int b) {
        if (b == 0) return a;
        return gcd(b, a % b);
    }
    
    public static void main(String[] args) {
        n = cin.nextInt();
        //读取值并求得gcd公约数
        int d = 0;
        for (int i = 1; i <= n; i ++ ) {
            w[i] = cin.nextInt();
            d = gcd(d, w[i]);
        }
        if (d != 1) {
            System.out.println("INF");
        }else {
            f[0] = true;
            for (int i = 1; i <= n; i ++) {
                for (int j = 0; j <= 10000; j ++) {
                    f[j] = f[j];
                    if (j >= w[i]) f[j] |= f[j - w[i]];
                }
            }
            int ans = 0;
            for (int j = 0; j <= 10000; j ++) 
                if (!f[j]) ans++;
            System.out.println(ans);
        }
    }
    
}

习题2：AcWing 1070. 括号配对（中等，区间DP）

题目链接：AcWing 1070. 括号配对

分析

实际上该题是密码脱落的一个扩展，不仅仅[()]符合GRE，[]()也是符合的。

两种DP思路：

思路1：状态表示的属性就是本题目标于要求的添加匹配的最小值

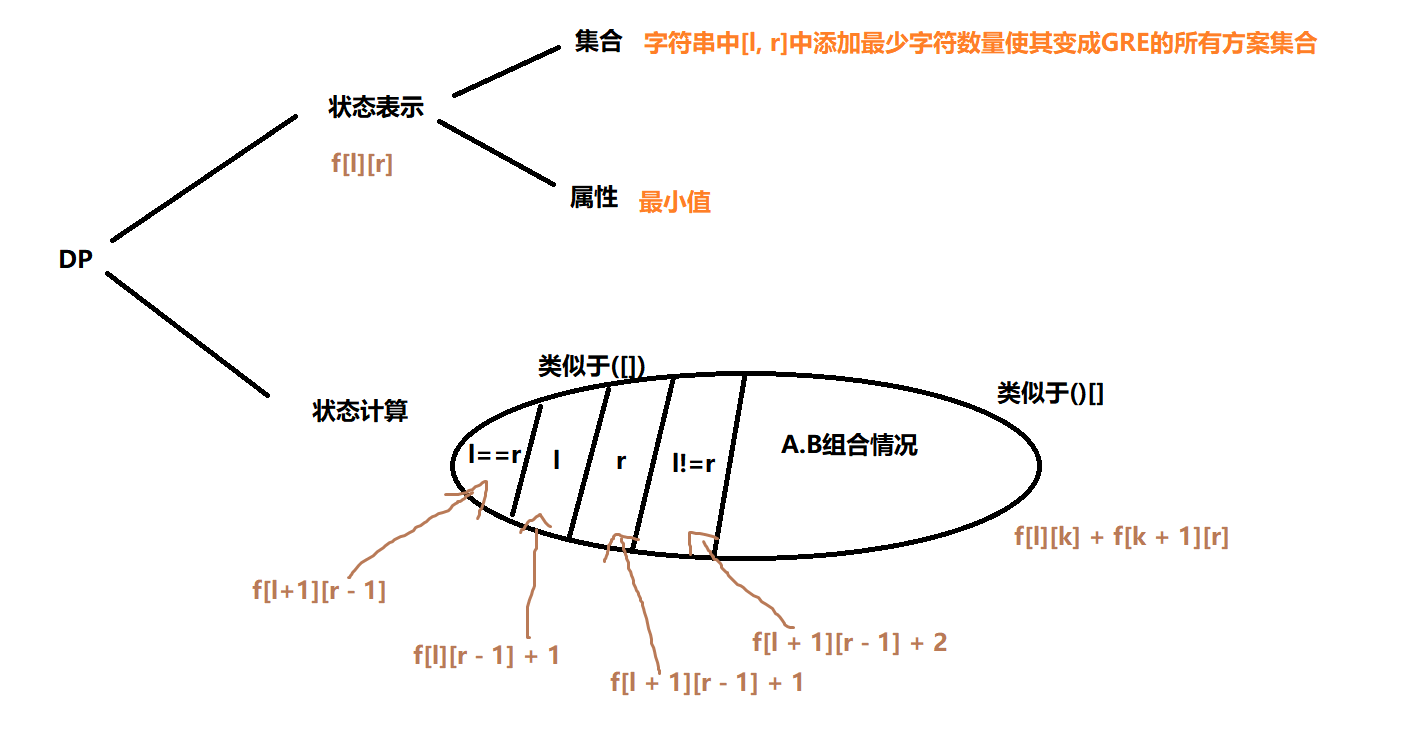
状态定义：dp(i, j)

转移方程：

回文情况：（类似于([])）
- l==r（左右两端相同，则无需添加字符）：dp(l + 1, r - 1)
- 选择r点（r点需要添加一个匹配）：dp(l, r- 1) + 1
- 选择l点（l点需要添加一个匹配）：dp(l + 1, r) + 1
- l!=r（左右两端不相同，则需要添加两个字符）：dp(l + 1, r - 1) + 2
组合情况：类似于()[]
- Math.min(f(l, k) + f(k + 1, r))【k∈[0, r]】

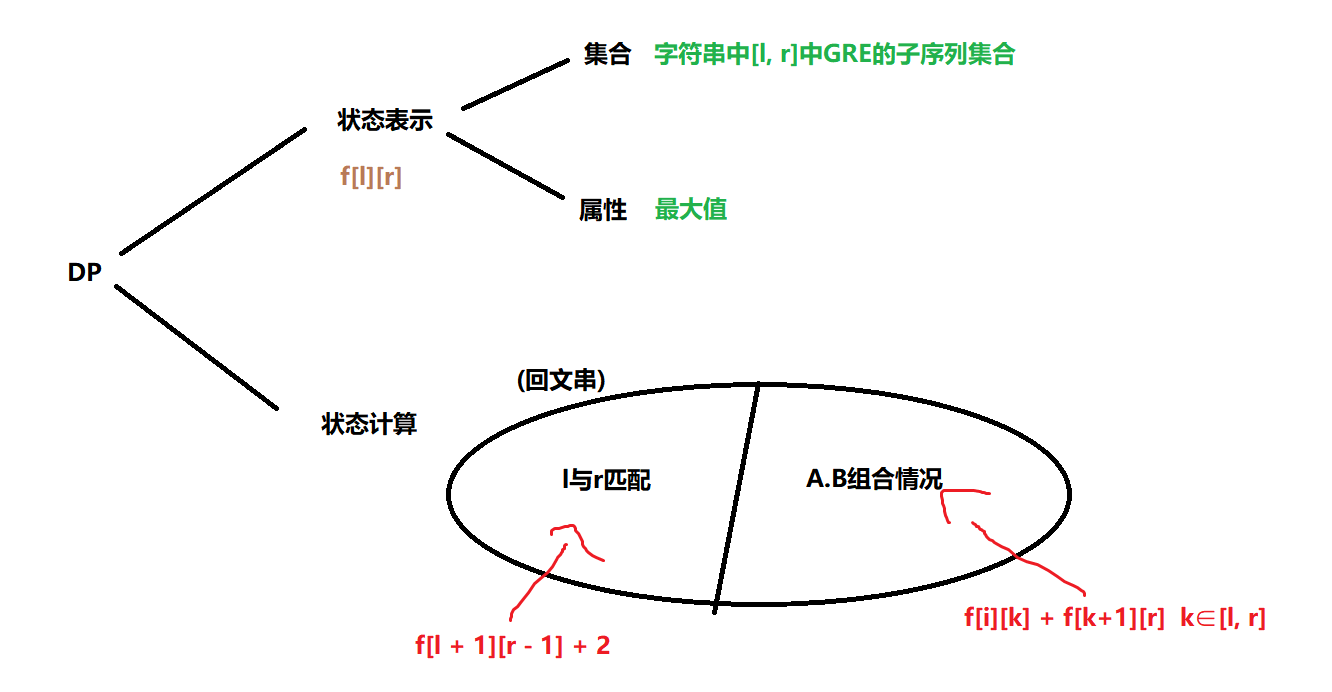
思路2：状态表示的属性指的是在l-r区间中能够组成GRE的最大数量

添加的最少字符数 = 总字符数 - 可组成GRE最大数量

整体思路与例题3大致相同。

题解1：区间DP（DP状态表示最小值）

复杂度分析：时间复杂度O(n³)；空间复杂度O(n²)

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static final int n = 110, INF = 10000;
    //字符数组
    static char[] arr;
    //dp
    static int[][] f = new int[n][n];
    
    //检查两端点是否相等
    public static boolean check(int l, int r) {
        if (arr[l] == '(' && arr[r] == ')') return true;
        if (arr[l] == '[' && arr[r] == ']') return true;
        return false;
    }
    
    public static void main(String[] args) {
        arr = cin.next().toCharArray();
        int n = arr.length;
        //初始化，单个字符需要添加1个
        for (int i = 0; i < n; i ++) f[i][i] = 1;
        
        for (int len = 2; len <= n; len++) {
            for (int l = 0; l + len - 1 < n; l ++) {
                int r = l + len - 1;
                //设置初始值
                f[l][r] = INF;
                //([])包含问题
                //若是左右两端点包含，那么表示无需添加
                if (check(l, r)) f[l][r] = f[l + 1][r - 1];
                //避免一个越界情况（添加初始化及len=2时即可无需判断）
                //if (r >= 1) {
                    //f[l][r - 1] + 1     f[l + 1][r] + 1    f[l][r]取最小值
                    f[l][r] = Math.min(Math.min(f[l][r - 1], f[l + 1][r]) + 1, f[l][r]);
                //}
                //组合问题
                for (int k = l; k <= r; k ++) {
                    f[l][r] = Math.min(f[l][r], f[l][k] + f[k + 1][r]);
                }
            }
        }
        System.out.println(f[0][n - 1]);
    }
    
}

题解2：区间DP（DP状态表示最大值）

复杂度分析：时间复杂度O(n³)；空间复杂度O(n²)

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static final int n = 110, INF = 10000;
    //字符数组
    static char[] arr;
    //dp
    static int[][] f = new int[n][n];
    
    //检查两端点是否相等
    public static boolean check(int l, int r) {
        if (arr[l] == '(' && arr[r] == ')') return true;
        if (arr[l] == '[' && arr[r] == ']') return true;
        return false;
    }
    
    public static void main(String[] args) {
        arr = cin.next().toCharArray();
        int n = arr.length;
        //初始化，单个字符并不属于GRE，所以初始化为0，原本就是0就无需初始化
        //for (int i = 0; i < n; i ++) f[i][i] = 0;
        
        for (int len = 1; len <= n; len++) {
            for (int l = 0; l + len - 1 < n; l ++) {
                int r = l + len - 1;
                if (len > 1) {
                    //回文串问题
                    if (check(l, r)) f[l][r] = Math.max(f[l + 1][r - 1] + 2, f[l][r]);
                    //实际可省略
                    // if (f[l + 1][r] > f[l][r]) f[l][r] = f[l + 1][r];
                    // if (f[l][r - 1] > f[l][r]) f[l][r] = f[l][r - 1]; 
                    //组合问题
                    for (int k = l; k <= r; k ++) {
                        f[l][r] = Math.max(f[l][r], f[l][k] + f[k + 1][r]);
                    }   
                }
            }
        }
        System.out.println(n - f[0][n - 1]);
    }
    
}

习题3：AcWing 1078. 旅游规划（树型DP）

题目链接：AcWing 1078. 旅游规划

分析

本题实际上让我们找到树的所有直径上的节点。

思路：首先就是需要确定树的最大直径，然后就是找到所有最大直径路径上的点。

那么如何确定在直径路径上的点呢？

计算得到一个结点向下的一条最大路径(包含次大的)及向上的最大路径。
最终遍历一遍所有节点，拿到该结点下方的最大值+上方的最大值，若是相加的值为树的直径，那么表示该节点属于最大直径上的点。

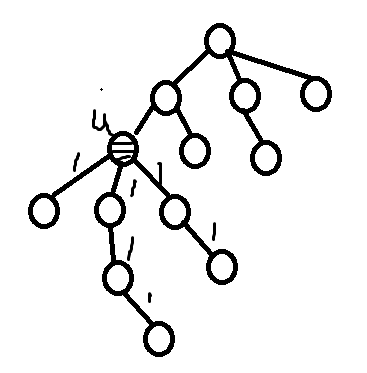
对于代码中的搜索节点下方最大距离和节点上方的最大距离有几个点来进行图示说明：

①节点之下：对于确定某个节点自下而上的最大距离和次大距离，记录长度从最底部开始向上延伸

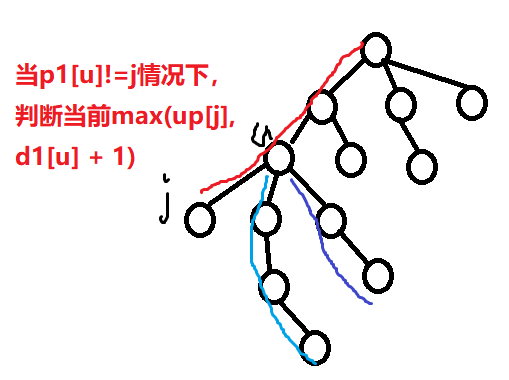
②节点之上：对于看某个点的向上的最大路径，两种情况如下所示

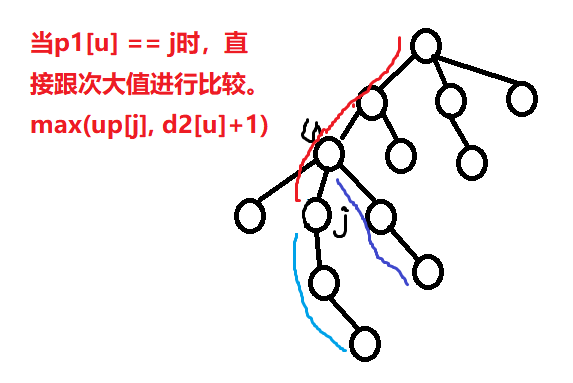
题解：树型DP及树的直径

复杂度分析：时间复杂度O(n)；空间复杂度O(1)

import java.io.*;
import java.util.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 200010, M = N * 2;
    //邻接表存储图，单链表数组写法
    static int[] e = new int[M], ne = new int[M], h = new int[N];
    static int idx;
    //存储节点向下的最大距离d1(含最大距离的最近节点p1)及次大距离d2；节点向上的最大距离up
    static int[] d1 = new int[N], d2 = new int[N], p1 = new int[N], up = new int[N];
    //树的直径
    static int maxd;
    //输入n长度
    static int n;
    
    //找寻节点向下的最大距离与次大距离
    public static void dfs_down(int u, int f) {
        //遍历所有节点
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            //不重复搜索
            if (j != f) {
                //先进行递归
                dfs_down(j, u);
                //进行从上至上距离增加
                int distance = d1[j] + 1;
                //若是当前距离>最大值，更新最大值和次大值
                if (distance > d1[u]) {
                    d2[u] = d1[u];
                    d1[u] = distance;
                    p1[u] = j;
                }else if (distance > d2[u]) { //若是当前距离>次大值，更新次大值
                    d2[u] = distance;
                }
            }
        }
        maxd = Math.max(maxd, d1[u] + d2[u]);
    }
    
    //找寻节点向上的最大距离
    public static void dfs_up(int u, int f) {
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j != f) {
                //从上向下开始距离增加
                up[j] = up[u] + 1;
                //若是u节点的向下的最大节点为j，那么直接去进行比较次大值及当前up[j]
                //不选择原先的向下的最大路径避免重复，此时选择次大值
                if (p1[u] == j) {
                    up[j] = Math.max(up[j], d2[u] + 1);
                }else {
                    //若当前往下并不是之前最大点，那么实际上就可以将之前节点下方的最大路径
                    up[j] = Math.max(up[j], d1[u] + 1);
                }
                dfs_up(j, u);
            }
        }
    }
    
    //添加到邻接表中
    public static void add (int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    
    public static void main (String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine());
        
        //初始化头部结点
        Arrays.fill(h, -1);
        
        for (int i = 1; i < n; i ++ ) {
            String[] ss = cin.readLine().split(" ");
            int a = Integer.parseInt(ss[0]);
            int b = Integer.parseInt(ss[1]);
            //添加到邻接表中
            add(a, b);
            add(b, a);
        }
        
        //向下进行搜索取得树的直径、每个节点向下的最大路径值及次大路径值
        dfs_down(0, - 1);
        
        //向上来进行搜索，取得每个节点的上方的最大路径
        dfs_up(0, -1);
        
        //遍历所有节点，找到节点上方最大路径、节点下方最大及次大路径中的两个最大长度进行相加
        //若是相加值为树的直径，那么该结点就需要显示
        //System.out.printf("maxd : %d\n", maxd);
        for (int i = 0; i < n; i ++) {
            int[] paths = {d1[i], d2[i], up[i]};
            Arrays.sort(paths, 0, 3);
            //选择最大的两个路径值合并
            if (paths[1] + paths[2] == maxd) {
                System.out.println(i);
            }
        }
        
    }
    
}

习题4：AcWing 1217. 垒骰子（中等，蓝桥杯）

题目链接：AcWing 1217. 垒骰子

分析

简述：本题一开始采用DP思路，接着将其转为矩阵乘法，进而使用矩阵快速幂来AC。

本题首先不考虑数据量可以使用线性DP来进行解决。

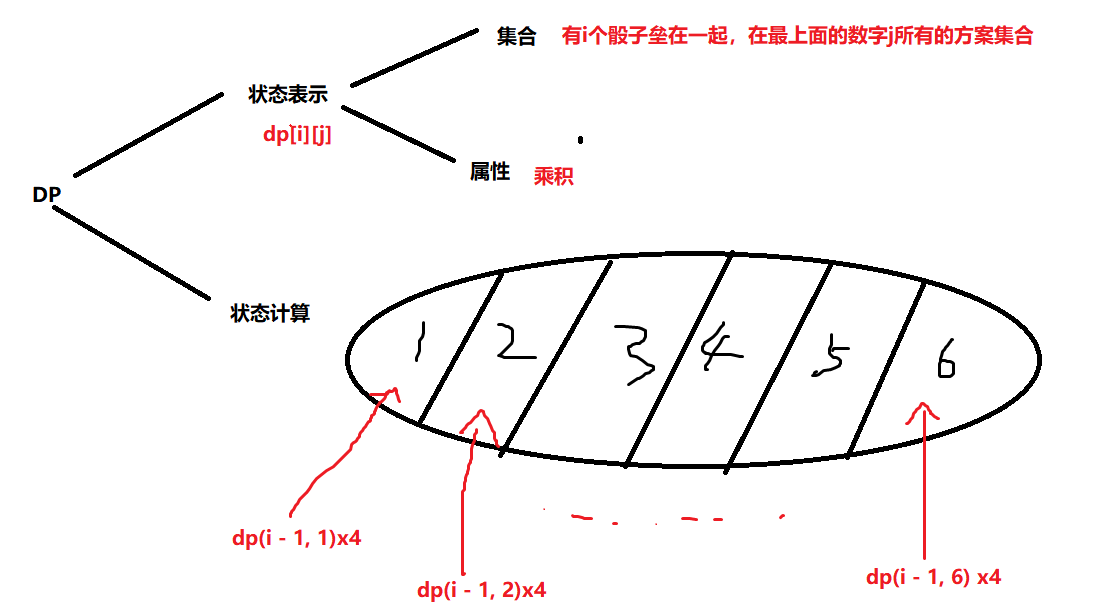
for (int i = 2; i <= n; i++)
    for (int j = 1; j <= 6; j++)
        if (非互斥) dp[i][j] = (dp[i][j] + dp[i - 1][j] * 4)

若是使用线性DP，题目给出的n长度为10亿，O(n)复杂度是肯定会超时的，所以我们需要再进行优化将其优化为O(logn)来进行ac。

本题实际上可以发现可以将dp[i][j]二维数组计算来转为一个一维f(i)乘上一个矩阵，这个矩阵中就包含了6个点分别不同的情况。

fn默认为 $\left[\begin {array}{c} 4 &4 &4 &4 &4 &4 \end{array}\right]$ 。表示的是最底部一组的情况。

默认若是无互斥情况，累乘矩阵为： $\left[\begin {array}{c} 4 &4 &4 &4 &4 &4 \\ 4 &4 &4 &4 &4 &4 \\ 4 &4 &4 &4 &4 &4 \\ 4 &4 &4 &4 &4 &4 \\ 4 &4 &4 &4 &4 &4\end{array}\right]$

按照题目给出的样例：有一组互斥，即为1与2

2 1
1 2

又筛子对应面规定：1-4、2-5、3-6

那么若是f(i-1)的顶部筛子数为1，那么f(i)的顶部就不能够为5，因为5的底部为2，2与1是互斥的。

所以我们的矩阵就变为： $\left[\begin {array}{c} 4 &4 &4 &4 &4 &4 \\ 4 &4 &4 &4 &4 &4 \\ 4 &4 &4 &4 &4 &4 \\ 4 &4 &4 &4 &4 &4 \\ 0 &4 &4 &4 &4 &4\end{array}\right]$ 。con[1][5] = 0

那么我们就可以列出公式：f(n) = f(1) * A^n-1，此时我们对应矩阵乘法可以采取矩阵快速幂来进行优化时间复杂度为O(logn)。

对于矩阵乘法以及矩阵快速幂的实现可见该博客：快速幂及矩阵快速幂分析及代码实现

最终的一个时间复杂度主要就是矩阵乘法累乘36*36*log(n)，基本就是少于一万次运算，即可AC该题。

对于矩阵乘法只写一个函数的小优化：原本要写两个函数，一个函数是一维乘二维，另一个函数是二维乘二维，实际上可以将一维扩充成二维，除了第一行其他都是0即可，这样我们只需要写一个二维乘二维的函数即可。

题解：线性DP，矩阵快速幂

复杂度分析：时间复杂度O(logn)；空间复杂度O(1)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 6, MOD = (int)1e9 + 7;
    static int n, m;
    //乘法矩阵A
    static int[][] A = {
        {4, 4, 4, 4, 4, 4},
        {4, 4, 4, 4, 4, 4},
        {4, 4, 4, 4, 4, 4},
        {4, 4, 4, 4, 4, 4},
        {4, 4, 4, 4, 4, 4},
        {4, 4, 4, 4, 4, 4}
    };
    //f(n)
    static int[][] ans = {
        {4, 4, 4, 4, 4, 4},
        {0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 0}
    };
    
    //获取到数字x的对面
    public static int get_pos (int x) {
        if (x > 3) return x - 3;
        return x + 3;
    }
    
    //矩阵乘法
    public static void multi(int a[][], int b[][]) {
        //新建一个临时矩阵存储结果值
        int[][] temp = new int[N][N];
        //矩阵乘法
        for (int i = 0; i < N; i ++) {
            for (int j = 0; j < N; j ++) {
                for (int k = 0; k < N; k ++) {
                    temp[i][j] = (int)((temp[i][j] + a[i][k] * (long)b[k][j] % MOD) % MOD);
                }
            }
        }
        //拷贝到a数组中
        for (int i = 0; i < N; i ++ ) {
            for (int j = 0; j < N; j ++ ) {
                a[i][j] = temp[i][j];
            }
        }
    }
    
    
    
    public static void main(String[] args) throws Exception{
        String[] ss = cin.readLine().split(" ");
        n = Integer.parseInt(ss[0]);
        m = Integer.parseInt(ss[1]);
        //接收互斥面，根据互斥面来进行设置矩阵A的值
        for (int i = 0; i < m; i ++ ) {
            ss = cin.readLine().split(" ");
            int a = Integer.parseInt(ss[0]);
            int b = Integer.parseInt(ss[1]);
            A[get_pos(b) - 1][a - 1] = 0;
            A[get_pos(a) - 1][b - 1] = 0;
            //等价于 (y总写法)
            // a--;
            // b--;
            // A[a][get_pos(b)] = 0;
            // A[b][get_pos(a)] = 0;
        }
        
        //确认矩阵乘积次数为n-1
        //矩阵快速幂
        for (int k = n - 1; k != 0; k >>= 1) {
            if ((k & 1) == 1) multi(ans, A);
            multi(A, A);
        }
        
        //统计最终ans矩阵中的第一行相加
        int res = 0;
        for (int i = 0; i < N; i ++ ) {
            res = (res + ans[0][i]) % MOD;
        }
        System.out.println(res);
    }
}

参考文章

[1]. AcWing 1050. 鸣人的影分身：AcWing 1050. 鸣人的影分身、AcWing 1050. 模板题！！不是什么最小值是0，最小值是1 、AcWing 1050. 鸣人的影分身、AcWing 1050. 鸣人的影分身（蓝桥杯C++ AB组辅导课）

[2]. AcWing 1047. 糖果：AcWing 1047. 糖果、AcWing 1047. 背包问题（大白话详解）、AcWing 1047. 背包问题（大白话详解）、AcWing 1047. 糖果（深入理解不合法状态）、AcWing 1047. 糖果(java)

[3]. AcWing 1222.密码脱落：AcWing 1222. 密码脱落、AcWing 1222. 密码脱落（蓝桥杯C++ AB组辅导课）、AcWing 1222. 密码脱落、AcWing 1222. 区间DPDP（大白话详解）、AcWing 1222. 密码脱落（跟y总不一样的状态表示）、AcWing 1222. 密码脱落(java)

[4]. AcWing 1220. 生命之树：AcWing 1220. 生命之树、AcWing 1220. 生命之树、AcWing 1220. 生命之树（弄懂状态划分和状态计算）、AcWing 1220. 生命之树

[5]. AcWing 1303. 斐波那契前 n 项和：AcWing 1303. 斐波那契前 n 项和、AcWing 1303. 斐波那契前 n 项和——另一个更巧妙的解法、3.躲在厕所学：『矩阵法』求解斐波那契数列、AcWing 1303. 斐波那契前 n 项和（蓝桥杯C++ AB组辅导课）

[6]. 习题1 AcWing 1226. 包子凑数：AcWing 1226. 包子凑数、AcWing 1226. 包子凑数（闫式DP分析法 + 图 + 分析）、AcWing 1226. 包子凑数、AcWing 1226. 包子凑数完全背包 (yan氏dp+层层分析yan氏dp+层层分析)

[7]. 习题2：AcWing 1070. 括号配对：AcWing 1070. 括号配对、AcWing 1070. 括号配对区间dp−>yan氏dp+层层分析区间dp−>yan氏dp+层层分析、AcWing 1070. 括号配对、AcWing 1070. 括号配对、AcWing 1070. 括号配对（蓝桥杯C++ AB组辅导课）

[8]. 习题3：AcWing 1078. 旅游规划：AcWing 1078. 旅游规划、AcWing 1078. 旅游规划（蓝桥杯C++ AB组辅导课）

[9]. 习题4：AcWing 1217. 垒骰子：AcWing 1217. 垒骰子、AcWing 1217. 垒骰子(Java dfs+普通dp+矩阵快速幂)、AcWing 1217. 垒骰子（蓝桥杯C++ AB组辅导课）