文章目录
- 1、普通方式
- 1.1、普通计算过程
- 1.2、优化方式
- 2、图像中的情况
- 2.1、常规处理
- 2.2、opencv中的处理
- 2.2.1、cv::clipLine函数
- 2.2.2、测试代码
- 2.2.3、测试结果
1、普通方式
已知矩形框左上(x1,y1)、右下(x2,y2)点,直线方程 y = kx+b,求交点。
这个问题转换为:计算直线与矩形框的四条线段的交点,因此最多执行4次。
首先计算直线与线段所在直线交点,若交点的在线段坐标的范围内,那么认为是有交点。
1.1、普通计算过程
这里不考虑直线平行的常规情况,如下
{
a
1
x
+
b
1
y
+
c
1
=
0
a
2
x
+
b
2
y
+
c
2
=
0
\left\{\begin{matrix} a_1x + b_1y+c_1 = 0 \\ a_2x + b_2y+c_2 = 0 \end{matrix}\right.
{a1x+b1y+c1=0a2x+b2y+c2=0
计算得到横坐标
x
=
b
2
c
1
−
b
1
c
2
b
2
a
1
−
b
1
a
2
x=\frac{b_2c_1 - b_1c_2}{b_2a_1-b_1a_2}
x=b2a1−b1a2b2c1−b1c2
当其位于某一条线段的横坐标坐标取值范围
x
∈
[
x
1
,
x
2
]
x \in [x_1, x_2]
x∈[x1,x2] 时,认为存在交点
{
x
=
b
2
c
1
−
b
1
c
2
b
2
a
1
−
b
1
a
2
y
=
−
a
2
x
−
c
2
b
2
\left\{\begin{matrix} x=\frac{b_2c_1 - b_1c_2}{b_2a_1-b_1a_2} \\ y = \frac{-a_2x-c_2}{b_2} \end{matrix}\right.
{x=b2a1−b1a2b2c1−b1c2y=b2−a2x−c2
1.2、优化方式
我们分两种情况。直线垂直和水平,以及普通情况。
-
(1)垂直和水平情况
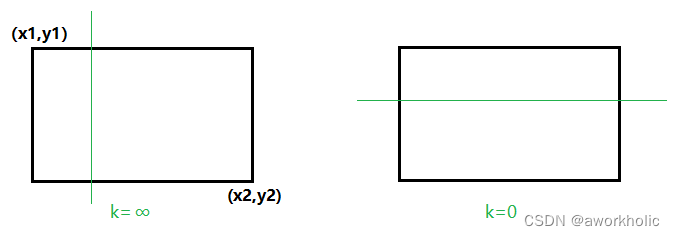
这种方式简单,当垂直时直线 x = m x = m x=m,若 m ∈ [ x 1 , x 2 ] m \in [x_1, x_2] m∈[x1,x2],那么交点为 ( m , y 1 ) (m,y_1) (m,y1)、 ( m , y 2 ) (m,y_2) (m,y2);同理,当水平式直线 y = n y = n y=n,若 n ∈ [ y 1 , y 2 ] n \in [y_1, y_2] n∈[y1,y2],那么交点为 ( x 1 , n ) (x_1,n) (x1,n)、 ( x 2 , n ) (x_2,n) (x2,n)。 -
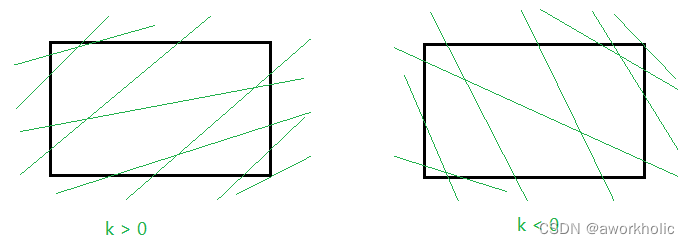
(2)不相交时
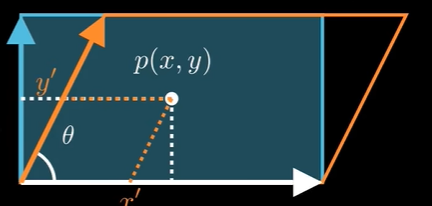
在下图中我们绘制斜率分别为正、负的情况,且与矩形不相交的示意图,大概有8种情况下,矩形框的4个顶点均在某条直线的一侧。
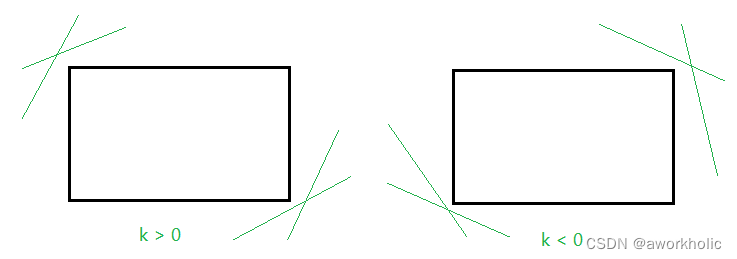
因此,我们判断直线是否与矩形相交,可以直接判定矩形框四个顶点 ( x 1 , y 1 ) , ( x 2 , y 1 ) , ( x 2 , y 2 ) , ( x 1 , y 2 ) (x_1,y_1),(x_2,y_1),(x_2,y_2),(x_1,y_2) (x1,y1),(x2,y1),(x2,y2),(x1,y2) 以顺时针带入直线方程函数 f ( x , y ) = a x + b y + c f(x,y) = ax+by+c f(x,y)=ax+by+c 的结果是否都同号即可。 -
(3)相交时
在下图中绘制了所有相交的情况,可以看到 在(2)基础上,直线与矩形框线段有交点时,矩形框2个顶点一定在直线的两侧,或者某个端点在直线上。
我们顺时针将矩形框框四个顶点 ( x 1 , y 1 ) , ( x 2 , y 1 ) , ( x 2 , y 2 ) , ( x 1 , y 2 ) (x_1,y_1),(x_2,y_1),(x_2,y_2),(x_1,y_2) (x1,y1),(x2,y1),(x2,y2),(x1,y2) 带入直线方程函数 f ( x , y ) = a x + b y + c f(x,y) = ax+by+c f(x,y)=ax+by+c ,若相邻两个点符号不同(不同为正,不同为负;或 +、-、0的组合),认为是有交点的。
图像中矩形看过顶点已知,且边界线为水平线和垂直线,因此计算简单。
直线方程为
y
=
k
x
+
b
y = kx + b
y=kx+b,矩形框边界的线按顺时针排列:水平线
y
=
y
1
y = y_1
y=y1, 垂直线
x
=
x
2
x = x_2
x=x2,水平线
y
=
y
2
y=y_2
y=y2, 垂直线
x
=
x
1
x = x_1
x=x1。 后面计算过程,不做赘述。
2、图像中的情况
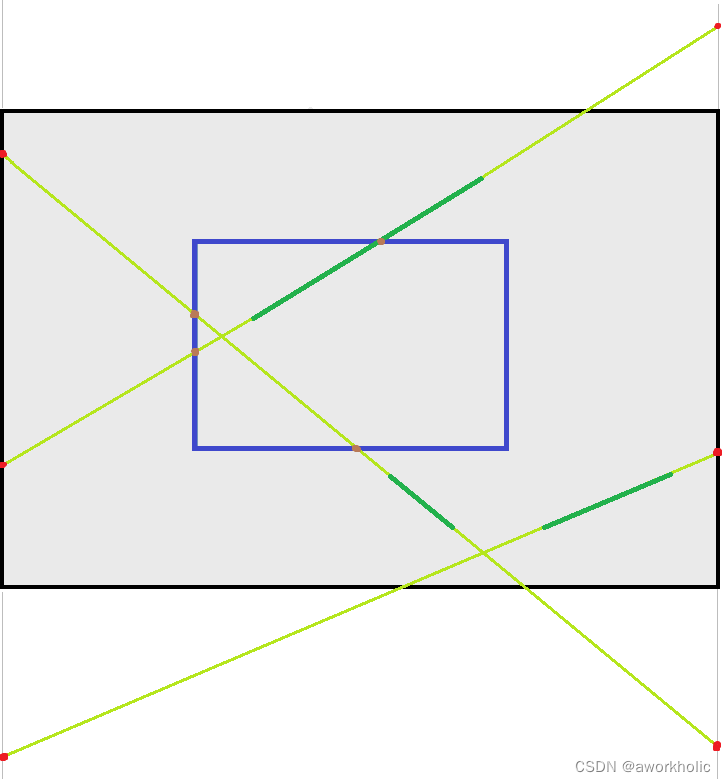
这里直线与矩形框的交点,我们考虑并非线段(若直线延长后与矩形框有交点,如果用两个点描述直线必须要求延长后与矩形框有交点),而是延长后的线段作为实际直线。
通常矩形框在画面中,例如下图中黑框灰色区域(宽度w)为画面区域,蓝色矩形框位于其中。绿色为线段,延长后与矩形框相交为棕色点。
2.1、常规处理
通常我们计算的逻辑,会考虑直线在画面中的多种情况,例如 垂直、水平,以及实际与画面无交集的无效直线等。
可以参考前述计算方式,这里不在赘叙。
2.2、opencv中的处理
我们直接以图像x方向左、右边界作为线段的延长线,得到两点(0, y0)和(w, y1),之后使用cv::clipLine()计算交点。
2.2.1、cv::clipLine函数
先给出函数定义
bool clipLine( // true if any part of line in imgRect
cv::Rect imgRect, // rectangle to clip to
cv::Point& pt1, // first endpoint of line overwritten
cv::Point& pt2 // second endpoint of line, overwritten
);
bool clipLine( // true if any part of line in image size
cv::Size imgSize, // size of image,implies rectangle at 0,0
cv::Point& pt1, // first endpoint of line,overwritten
cv::Point& pt2 // second endpoint of line,overwritten
);
第一种函数的形式使用了cv::Rect,直线和这个矩形比较;第二个函数只有cv::Size,该形式表示矩形的范围是从(0,0)开始的。
只有当喜爱那段完全在指定的矩形范围之外时,函数cv::clipLine()才会返回false。
注意,端点是引用,当线段与矩形框相交时,函数返回true,并改写pt1和pt2.
2.2.2、测试代码
首先Mat创建一个800x800的画面区域, 之后创建一个 cv::Rect(100, 100, 400, 400) 区域。
我们流程如下:
- 直线方程:通过2个点,使用
cv::fitLine拟合出直线的方程 - 线段端点:之后以图像左、右边界,确定直线的两个端点
- 求解交点: 使用
cv::clipLine计算矩形区域与线段的交点
完整测试代码如下
{
cv::Mat img(800, 800, CV_8UC3, {255,255,255});
cv::Rect rect(100, 100, 400, 400);
cv::rectangle(img, rect, {0,0,0}, 3);
// ---- 直线拟合
cv::Point temp[2] = {{100, 100}, {50,-100}};
cv::Vec4f line_para;
cv::fitLine(std::vector<cv::Point>{ temp[0], temp[1]/*{-40,-20},{810,830}*/}, line_para, cv::DIST_L2, 0, 1e-2, 1e-2);
// ---- 直线端点
cv::Point point0(line_para[2], line_para[3]);
//计算直线的端点(y = k(x - x0) + y0)
cv::Point point1, point2;
if(line_para[1] == 1 || line_para[1] == -1 ) {
point1 = cv::Point(line_para[2],0);
point2 = cv::Point(line_para[2], img.rows);
}
else {
float k = line_para[1] / line_para[0];
point1.x = 0;
point1.y = k * (0 - point0.x) + point0.y;
point2.x = img.cols;
point2.y = k * (point2.x - point0.x) + point0.y;
}
cv::Point line1[] = {point1,point2};
cv::line(img, line1[0], line1[1], {255,0,0},2);
// ----- 直线与矩形框交点
if(cv::clipLine(rect, line1[0], line1[1])) {
cv::circle(img, line1[0], 3, {0,0,255}, -1);
cv::circle(img, line1[1], 3, {0,0,255}, -1);
}
// -- 绘制
cv::circle(img, temp[0], 4, {0,255,0}, 2);
cv::circle(img, temp[1], 4, {0,255,0}, 2);
cv::imshow("1",img);
cv::waitKey(0);
return 0;
}
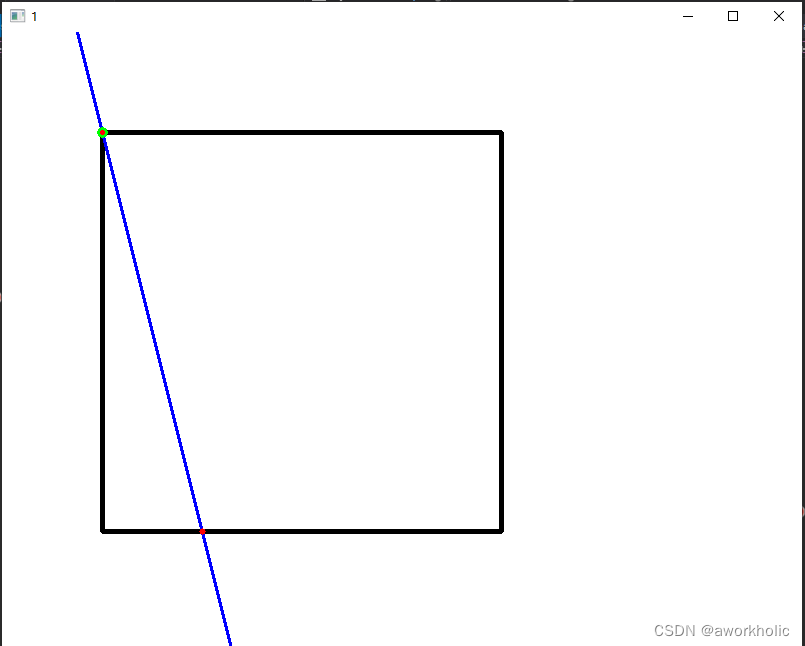
2.2.3、测试结果
测试结果如下图。实测任何对与任何直线,以上代码都能适用。