分类



要素

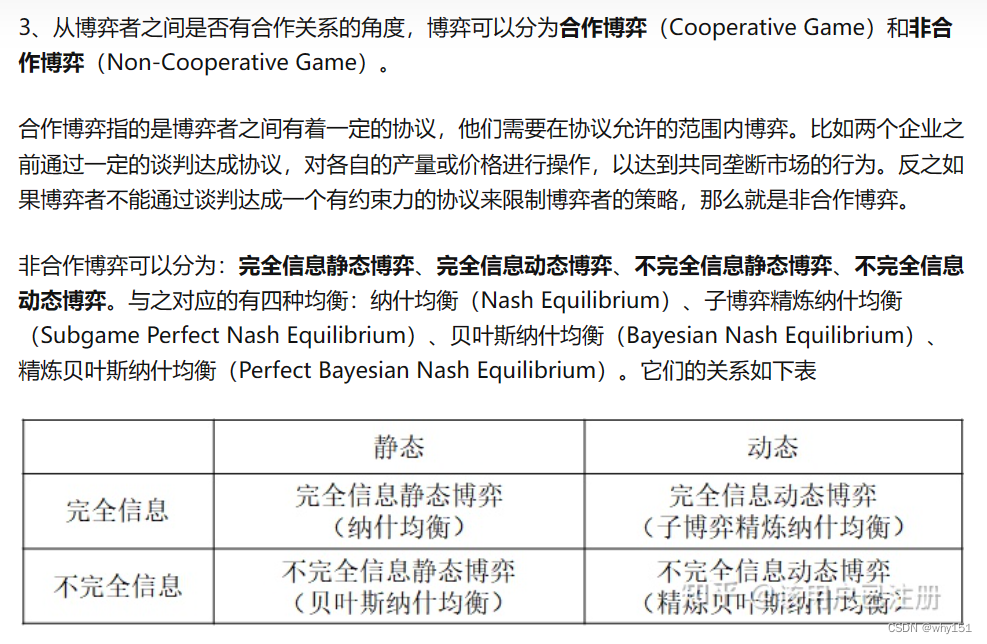
常见博弈

完全信息静态博弈

纳什均衡

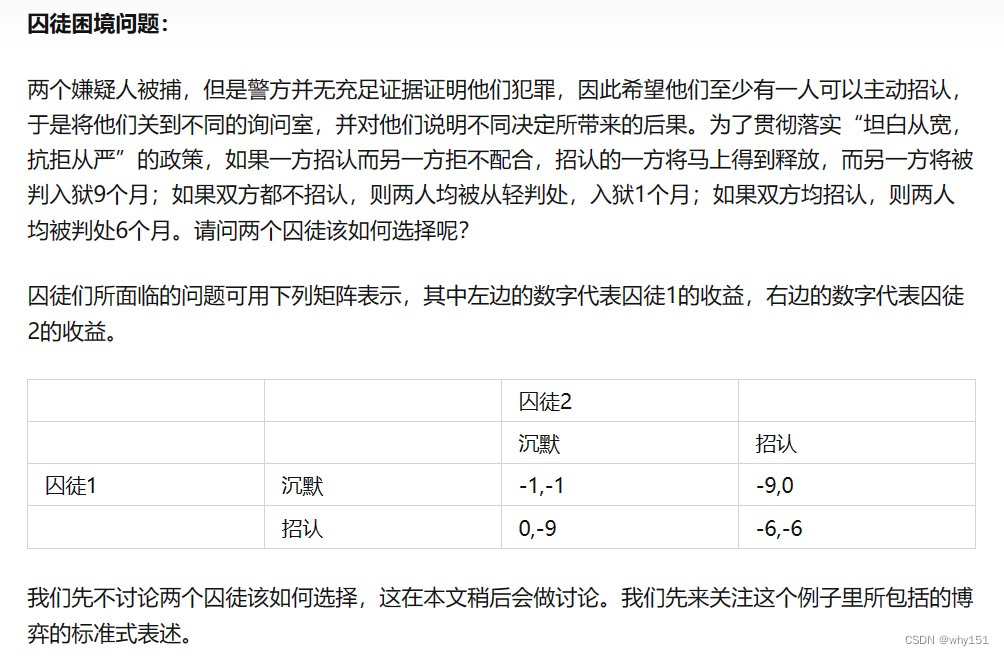
囚徒困境


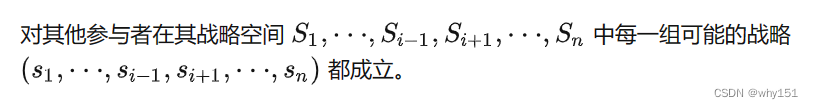
古诺双寡头模型

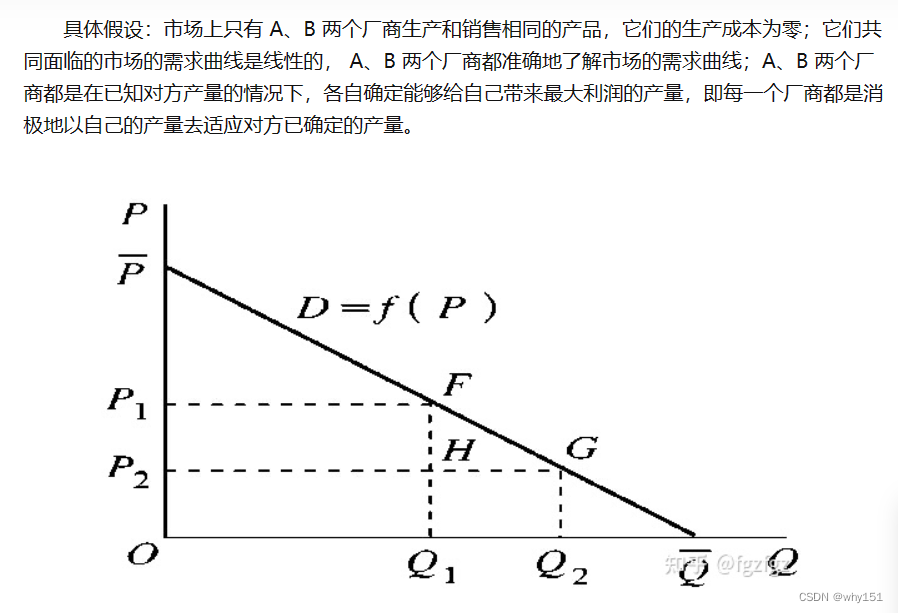







古诺双寡头模型的条件
- 市场中有且仅有两家公司
- 策略为同质商品的量, q i q_i qi
- 边际成本为c,生产成本就为c*q,在这里我们的边际成本是常数。
- 需求曲线: P = a − b ∗ ( q 1 + q 2 ) P=a-b*(q_1+q_2) P=a−b∗(q1+q2)
- 利润: U 1 ( q 1 , q 2 ) = P ∗ q 1 − c ∗ q 1 , U 2 ( q 2 , q 1 ) = P ∗ q 2 − c ∗ q 2 U_1(q_1,q_2)=P*q_1-c*q_1,U_2(q_2,q_1)=P*q_2-c*q_2 U1(q1,q2)=P∗q1−c∗q1,U2(q2,q1)=P∗q2−c∗q2
化简后
U 1 ( q 1 , q 2 ) = a ∗ q 1 − b ∗ q 1 2 − b ∗ q 1 ∗ q 2 − c ∗ q 1 U_1(q_1,q_2)=a*q_1-b*q_1^2-b*q_1*q_2-c*q_1 U1(q1,q2)=a∗q1−b∗q12−b∗q1∗q2−c∗q1
U
2
(
q
2
,
q
1
)
=
a
∗
q
2
−
b
∗
q
2
2
−
b
∗
q
1
q
2
−
c
∗
q
2
U_2(q_2,q_1)=a*q_2-b*q_2^2-b*q_1q_2-c*q_2
U2(q2,q1)=a∗q2−b∗q22−b∗q1q2−c∗q2

古诺双寡头模型的纳什均衡计算
要解纳什均衡点,首先我们必须寻找最佳策略,在这里我们就不能依靠猜测+论证的方式去寻找最佳策略,我们需要依靠计算。已知公司的收益为U,我们只需要求得U的最大值就可以找到最佳策略。寻找U的最大值的办法是求导 。
B R 1 : a − 2 ∗ b ∗ q 1 − b ∗ q 2 − c = 0 = > q 1 = a − b ∗ q 2 − c 2 ∗ b BR_1: a-2*b*q_1-b*q_2-c=0 => q_1=\frac{a-b*q_2-c}{2*b} BR1:a−2∗b∗q1−b∗q2−c=0=>q1=2∗ba−b∗q2−c
B R 2 : a − 2 ∗ b ∗ q 2 − b ∗ q 1 − c = 0 = > q 2 = a − b ∗ q 1 − c 2 ∗ b BR_2: a-2*b*q_2-b*q_1-c=0 => q_2=\frac{a-b*q_1-c}{2*b} BR2:a−2∗b∗q2−b∗q1−c=0=>q2=2∗ba−b∗q1−c
把 B R 1 , B R 2 BR_1,BR_2 BR1,BR2联立,求出两条直线的交点,这个交点就是纳什均衡点。
Cournot模型
该模型研究了寡头垄断市场中,企业追求利润最大化时的决策问题。其包含以下假设:
- 企业生产的产品是同质无差异的。该假设意味着消费者在购买企业生产的产品时,仅根据产品的价格进行决策,即谁的价格低就购买谁的产品;
- 企业进行的是产量竞争,也就是说,企业的决策变量为产量;
- 模型为静态的,即企业的行动是同时的。

一个企业增加产量,另一个企业就必须减少产量,因此,从这个意义上来说,Cournot模型中参与人的战略是相互替代的。
实际上,并不是任一个Cournot模型的Nash均衡都是存在的,且即使存在也不一定唯一。要使得Cournot模型中稳定的均衡存在且唯一是有条件的:要求两个企业的反应函数满足一定的条件。因为反应函数由利润函数和成本函数决定,因此要求利润函数和成本函数满足一定的条件。
联合垄断
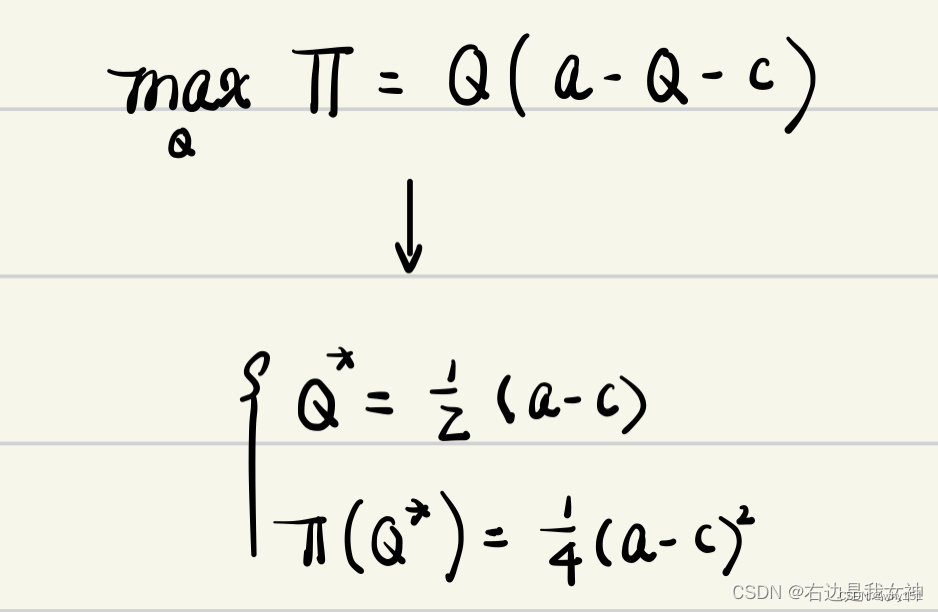

Betrand模型
在寡头垄断市场中,企业关心更多的可能是自己的产品在市场上的价格,而不是生产多少产品,也就是说,企业进行的可能是价格竞争而不是产量竞争。
和Cournot模型的区别:决策变量为价格。其余无差异。