本文ppt来自深蓝学院《机器人中的数值优化》
目录
1 Why Quasi-Newton Methods
2 Rate of convergence
3 Quasi-Newton Methods
3.1 Quasi-Newton approximation
3.2 preserve descent direction
3.3 secant condition
3.4 iterate B
3.5 Parsed solution B
4 Contrast Newton Methods and Quasi-Newton Methods
1 Why Quasi-Newton Methods

最速下降法需要消耗O(N)的时间复杂度,牛顿法需要O(N2),线性求解器更需要O(N3),我们需要找到一个时间复杂度较低的算法
比如机器人导航领域中常见的目标函数都是非线性的,用二次去拟合其实效果并不好,导致牛顿法在离最优解较远的地方就耗费了大量去计算二阶信息的时间
hessian矩阵也经常出现条件数比较大的情况
在非凸问题上,hessian矩阵不定导致搜索方向不是下降方向
2 Rate of convergence
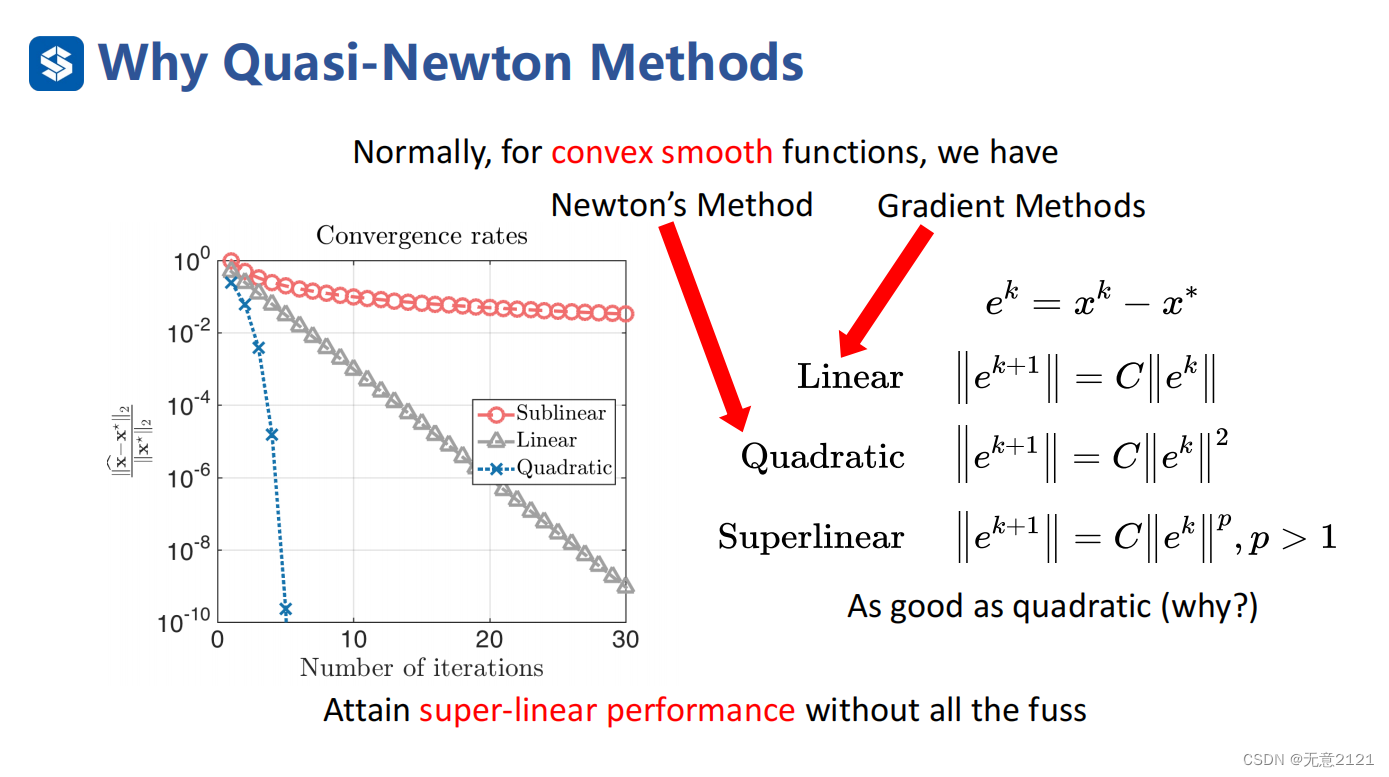 上述是评价一个算法优劣的一个指标,需要注意左图纵坐标是对数坐标系
上述是评价一个算法优劣的一个指标,需要注意左图纵坐标是对数坐标系
sublinear:亚线性收敛
Linear:线性收敛
Quadratic:二次收敛
Superlinear:超线性收敛
工程中,超线性收敛的算法就足够,单需要减少单次迭代的计算量
3 Quasi-Newton Methods
3.1 Quasi-Newton approximation
 是否能够让这个近似H的矩阵M把H中重要的信息都接收,不把所有二阶信息都接收
是否能够让这个近似H的矩阵M把H中重要的信息都接收,不把所有二阶信息都接收
由于线性方程求解耗费过多计算,能不能不用显示求解这个线性方程
希望这是一个不稠密的矩阵,不花掉N方的空间复杂度,只把重要信息存储,更加轻量化,易存储
一定要保存搜索方向是下降方向,同时保证能够包含曲率信息
3.2 preserve descent direction
 通过将搜索方向与负梯度方向内积大于0这一条件来判断搜索方向是否是下降方向,同时可以化简发现结果是一个二次型,只要M的逆是正定就能保证大于0,M的逆是正定那么M也一定正定
通过将搜索方向与负梯度方向内积大于0这一条件来判断搜索方向是否是下降方向,同时可以化简发现结果是一个二次型,只要M的逆是正定就能保证大于0,M的逆是正定那么M也一定正定
3.3 secant condition
 对梯度进行泰勒展开,再进行高阶无穷小的省略,就有如上的表达式,同时既然是估计,不如直接估计逆,省去线性求解的部分
对梯度进行泰勒展开,再进行高阶无穷小的省略,就有如上的表达式,同时既然是估计,不如直接估计逆,省去线性求解的部分
3.4 iterate B

这里可以表示成迭代优化的问题,首先假设这是凸函数的并且初始值给定
思路:B(k)已知,然后新的B需要和B(k)接近并且满足对称与正割条件(secant condition)
经过一轮一轮的迭代,x不仅在不断搜索接近最优解,B矩阵也是不断更新越来越接近真实的H
注意:新的B需要和B(k)接近这一目标函数会受尺度的影响,于是采用右图的方式消除scale的影响
3.5 Parsed solution B
 这就是B矩阵迭代的解析解,非常规则与优美,也有很多良好的性质,具体推导与性质可以参考原始论文,这里就不再赘述
这就是B矩阵迭代的解析解,非常规则与优美,也有很多良好的性质,具体推导与性质可以参考原始论文,这里就不再赘述
 这里是BFGS的算法框架(注意这是严格凸的情况,下面几篇文章将介绍非凸或非光滑的BFGS)
这里是BFGS的算法框架(注意这是严格凸的情况,下面几篇文章将介绍非凸或非光滑的BFGS)
4 Contrast Newton Methods and Quasi-Newton Methods
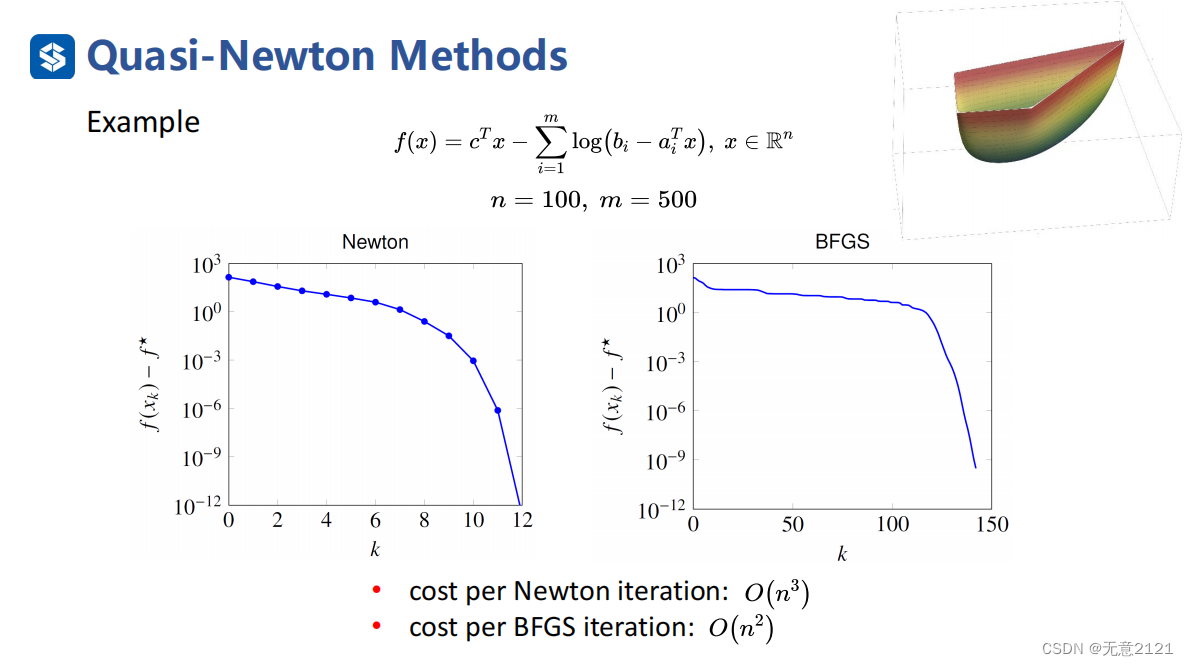
牛顿法达到了二次收敛的速率,BFGS达到了超线性收敛,但是一次iteration的时间复杂度是更快