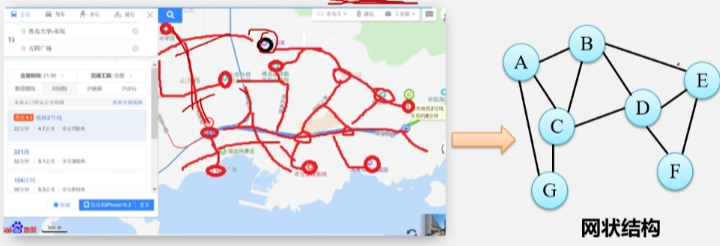
在所有参与者之间提供快速协议和团队合作的算法通过自组织网络系统实现有效的任务执行。

By Reza Olfati-Saber, Member IEEE, J. Alex Fax, and Richard M. Murray, Fellow IEEE

小于 翻译

摘要：本文提供了一个理论框架，用于分析多智能体网络系统的共识算法，重点是有向信息流的作用，由于链路/节点故障导致的网络拓扑变化的鲁棒性，时延和性能保证。概述了网络中信息共识的基本概念、算法的收敛方法和性能分析。我们的分析框架是基于矩阵理论、代数图理论和控制理论的工具。我们讨论了网络动态系统中的共识问题与各种应用之间的联系，包括耦合振荡器的同步、群集、编队控制、小世界网络中的快速共识、马尔可夫过程和基于八卦的算法、网络中的负载平衡、空间中的会合、传感器网络中的分布式传感器融合和信念传播。我们建立了复杂网络的频谱和结构特性与共识算法的信息扩散速度之间的直接联系。简要介绍了具有非局部信息流的网络系统，它比具有格子型最近邻交互的分布式系统快得多。仿真结果表明，在多车编队的协同控制中，采用小波约束约束对编队协同控制的作用。

关键字：共识算法;合作控制;植绒;图拉普拉斯算子;信息融合;多代理系统;网络控制系统;耦合振荡器的同步

1引言

共识问题在计算机科学中有着悠久的历史，并构成了分布式计算领域的基础 [1]。专家组共识问题的正式研究起源于 1960 年代的管理科学和统计学（参见 DeGroot [2] 和其中的参考文献）。二十年后，DeGroot 的统计共识理论思想再次出现在从多个传感器[3]和医学专家 [4]获得的具有不确定性的信息聚合中。

网络上的分布式计算在系统和控制理论方面具有传统，从 Borkar 和 Varaiya [5] 和 Tsitsiklis [6] 以及 Tsitsiklis、Bertsekas 和 Athans [7] 关于分布式决策系统和并行的异步渐近协议问题的开创性工作开始计算[8]。在代理网络（或动态系统）中，Bconsensus[ 意味着就一定数量的兴趣达成协议，这取决于所有代理的状态。共识算法 [（或协议）是一种交互规则，它指定代理与其网络上所有邻居之间的信息交换。

Olfati-Saber 和 Murray 介绍了提出和解决网络动态系统共识问题的理论框架在 [9] 和 [10] 中，建立在Fax 和 Murray [11]、[12] 早期工作的基础上。在不计算任何目标函数的情况下达成一致的对齐问题的研究出现在 Jadbabaie 等人的工作中 [13]。 [14] 和 [15] 中介绍了这项工作的进一步理论扩展，着眼于处理网络中的定向信息流，如图 1(a) 所示。

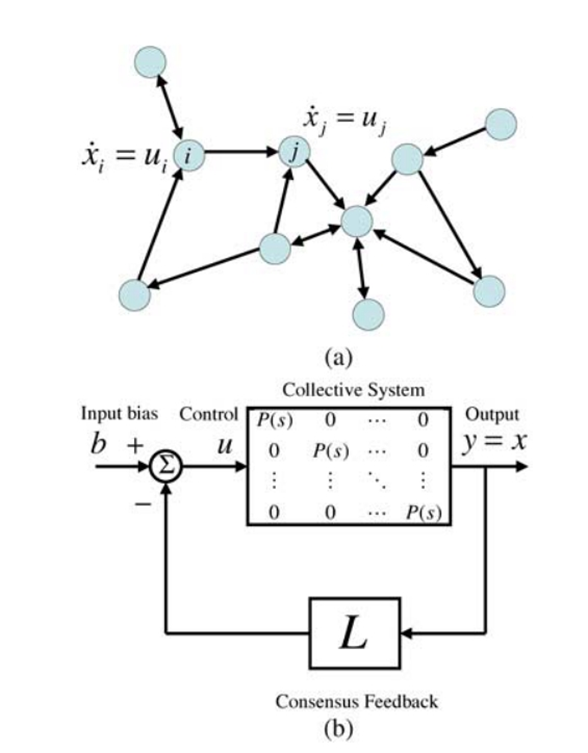
图 1. 两种等效形式的共识算法：(a) 一个集成代理网络，其中代理 i 接收其邻居代理 j 的状态 x_j，如果存在链接连接两个节点； (b) 具有相同传递函数  的互连动态系统网络的框图。集体网络系统具有对角传递函数，是一个多输入多输出（MIMO）线性系统。

[5]、[6] 和 [10] 中工作背后的共同动机是计算机科学中共识协议的丰富历史 [1]，而 Jadbabaie 等人[13] 试图提供对齐出现的正式分析在 Vicsek 等人[16] 的简化植绒模型中。 [10] 中的设置最初是基于设计基于代理的无定形计算机 [17]、[18] 的愿景创建的，用于网络中的协作信息处理。后来，[10] 被用于开发具有保证收敛性和处理障碍和对抗代理的能力的集群算法 [19]。

图拉普拉斯算子及其谱特性 [20]-[23] 是重要的图相关矩阵，在共识算法和对齐算法的收敛分析中起着至关重要的作用。图拉普拉斯算子是本文的一个重要关注点。值得一提的是，称为代数连通性的图拉普拉斯算子的第二小特征值量化了共识算法的收敛速度。图的代数连通性的概念已经出现在许多其他领域，包括信息论和通信中的低密度奇偶校验码 (LDPC) [24]、数论和量子混沌中的 Ramanujan 图 [25]，以及组合优化最大切割问题 [21] 等问题。

最近，来自不同工程和科学学科的研究人员对与多智能体网络系统相关的问题产生了极大的兴趣，这些问题与共识问题有着密切的联系。这包括如共识这样的主题[26] – [32] ，羊群和蜂群的集体行为 [19]，[33]–[37]，传感器融合 [38]–[40]，随机网络 [41]，[42] ，耦合振荡器的同步 [42]-[46]，复杂网络的代数连接 3 [47]-[49]，异步分布式算法 [30]，[50]，多机器人系统的编队控制 [51]-[59]，基于优化的协作控制[60]-[63]、动态图[64]-[67]、协调任务的复杂性[68]-[71]，以及贝叶斯网络中基于共识的信念传播[72]、[73]。稍后将对选定的应用程序进行详细讨论。

在本文中，我们重点介绍了五篇关键论文 Vnamely、Jadbabaie、L in、and Morse[13]、Olfati Saber 和 Murray [10]、Fax 和 Murray [12]、Moreau [14] 中描述的工作，以及 Ren 和 Beard [15]V，他们在为自组织网络系统或群体研究的最新进展铺平道路方面发挥了重要作用。这些联网系统由配备专用传感、计算和通信设备的本地交互移动/静态代理组成。因此，我们现在对复杂现象有了更好的理解，例如集群 [19]，或为传感器网络设计对节点和链路故障具有鲁棒性的新型信息融合算法 [38]、[72]–[76]。

基于 Gossip 的算法，例如推和协议 [77]，是计算机科学中基于拉普拉斯算子的共识算法的重要替代方案。马尔可夫过程在计算机科学家和控制理论家提出的这两类算法中的信息传播速度之间建立了有趣的联系 [78]。

本文的贡献是在一个统一的框架中对网络系统中共识问题的理论和应用的主要结果进行了连贯的概述。这包括信息共识中的基本概念和控制理论方法，用于严重依赖矩阵理论和谱图理论的共识协议的收敛和性能分析。该框架的一个副产品是证明文献 [10]、[12]-[15] 中看似不同的共识算法是密切相关的。本简介中讨论了共识问题在计算机科学、物理学、生物学、数学、机器人学和控制理论研究人员感兴趣的领域中的应用。

A. 网络共识

使用有向图表示代理网络的交互拓扑,其中，且。智能体 i 的邻接点用 Ni 表示，根据 [10]，一个简单的共识算法可以在图上表示为 n 个具有动态  的集成代理的状态达成协议。

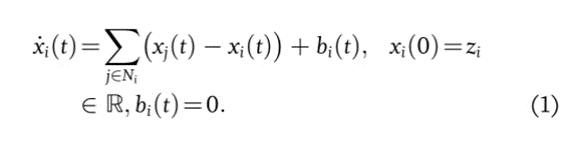
遵循协议 (1) 的代理组的集体动态可以写为

其中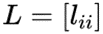是网络的拉普拉斯图，其元素定义如下：

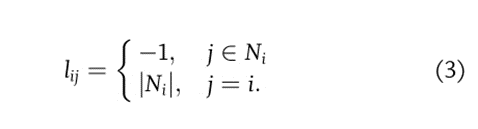
这里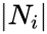，表示节点 i 的邻居数（或节点 i 的出度）。图 1 显示了 (1) 和 (2) 中具有标量状态的代理的共识算法的两种等效形式。图 1（b）中输入偏置 b 的作用稍后定义。

根据 (3) 中拉普拉斯图的定义，L 的所有行和都为零，因为。因此，L 始终具有零特征值。此零特征值对应于特征向量因为 1 属于的零空间。换句话说，系统(2)的平衡状态是所有节点都同意。基于代数图论 [23] 的分析工具，我们稍后证明是连接图的 (2) 的唯一平衡（直到常数乘法因子）。

可以证明，对于一个连通的网络，平衡点是全局指数稳定的。此外，共识值是等于初始值的平均值。这意味着无论每个智能体状态的初始值如何，所有智能体都会就函数的值达成渐近共识。

虽然的计算对于小型网络来说很简单，但它对超大型网络的影响更有趣。例如，如果一个网络有个节点，并且每个节点只能与 个邻居通信，则找到节点初始条件的平均值会更加复杂。协议（1）的作用是在如此大的网络中提供系统的共识机制来计算平均值。可以使用同步或异步分布式算法以类似方式计算多种函数（参见 [10]、[28]、[30]、[73]和[76]）。

B. f-共识问题和合作的意义

要了解合作在执行协调任务中的作用，我们需要区分无约束和约束共识问题。无约束共识问题只是对齐问题，其中所有代理的状态渐近相同就足够了。相反，在函数f(z)的分布式计算中，所有代理的状态必须渐近地变得等于f(z)，这意味着共识问题受到约束。我们将这个受约束的共识问题称为 f-共识问题。

解决 f-共识问题是一项合作任务，需要所有代理人自愿参与。为了证明这一事实，假设一个代理人决定不与其他代理人合作并保持其状态不变。然后，尽管其余代理达成一致，但整体任务无法执行。此外，可能存在形成联盟的多个代理不与其余代理合作的情况，并且删除该代理联盟及其链接可能会导致网络断开连接。在断开连接的网络中，所有节点都不可能达成一致（除非所有节点最初都同意，这是微不足道的情况）。

从上面的讨论中，合作可以被非正式地解释为同意提供一个人的状态并遵循为团体目标服务的共同协议。

有人可能认为解决对齐问题不是一项合作任务。理由是，如果一个代理人（称为领导者）保持其价值不变，则所有其他人将根据共识协议渐进地同意领导者并达成一致。但是，如果有多个领导者，其中两个意见不一致，则无法渐近达成共识。因此，对齐通常也是一项合作任务。

对涉及不止一种代理的系统行为的正式分析更为复杂，特别是在非合作博弈中存在对抗代理的情况下 [79]、[80]。本文的重点是协作多代理系统。

C. 迭代共识和马尔可夫链

在 [43] 中，Sepulcher 等人证明如果足够大，那么对于具有 all-to-all 链接的网络，所有初始状态都可以全局实现与对齐状态的同步。最近，在[45]中研究了可变时间延迟下网络振荡器的同步。我们相信，利用图拉普拉斯算子的光谱特性的收敛分析方法的使用将阐明振荡器网络中自同步的性能和收敛分析 [42]。

2）集群理论：配备传感和通信设备的移动代理集群可以作为移动传感器网络在环境中进行大规模分布式传感[87]。 OlfatiSaber [19] 开发了用于具有避障能力的移动代理的集群算法设计和分析的理论框架。共识算法在基于粒子的植绒中的作用是让代理实现与其邻居的速度匹配。在 [19] 中，证明了群是具有动态拓扑的动态系统网络。该拓扑是一个邻近图，它依赖于所有代理的状态，并且是在本地为每个代理确定的，即，flocks 的拓扑是一个状态依赖图。 Mesbahi [64] 在独立于集群的上下文中引入了状态依赖图的概念。

3）小世界中的快速共识：近年来，实现更快共识算法的网络设计问题引起了许多研究人员的广泛关注。在 Xiao 和 Boyd [88] 中，使用半定凸规划考虑并解决了网络权重的设计。这导致网络的代数连通性略有增加，这是衡量共识算法收敛速度的指标。另一种方法是保持权重固定并设计网络拓扑以实现相对较高的代数连通性。 Olfati-Saber [47] 基于 Watts 和 Strogatz [89] 的随机重新布线思想提出了一种用于网络设计的随机算法，这导致了他们著名的小世界模型的创建。网络现有链接的随意重新布线会产生相当快的共识算法。这是由于与格型最近邻图相比，网络的代数连通性增加了多个数量级。

4) 太空交会：共识问题的另一种常见形式是太空交会 [90]、[91]。这相当于通过位置诱导的交互拓扑（即邻近图）的多个代理达成位置共识。我们建议读者参考 [92] 和其中的参考资料进行详细讨论。这种类型的会合是一个不受约束的共识问题，在网络拓扑变化的情况下变得具有挑战性。集群比太空中的会合更具挑战性，因为它需要代理之间和代理与障碍物之间的碰撞避免。

5）传感器网络中的分布式传感器融合：共识问题的最新应用是传感器网络中的分布式传感器融合。这是通过提出各种分布式平均问题来实现的，这些问题需要实现卡尔曼滤波器 [38]、[39]、近似卡尔曼滤波器[74] 或线性最小二乘估计器 [75] 作为平均一致性问题。还开发了新的通过和高通共识滤波器，动态计算传感器网络中输入的平均值 [39]，[93]。

6) 分布式编队控制：多车辆系统因其商业和军事应用而成为网络系统的重要类别。分布式编队控制有两种广泛的方法：i) 将编队表示为刚性结构 [53]、[94]和使用从其结构势 [52] 获得的基于梯度的控制，以及 ii)使用矢量表示编队相邻车辆的相对位置和使用具有输入偏差的基于共识的控制器。我们在这里讨论后一种方法。