给定一个整数数组，它表示BST(即 二叉搜索树 )的 先序遍历 ，构造树并返回其根。

保证 对于给定的测试用例，总是有可能找到具有给定需求的二叉搜索树。

二叉搜索树 是一棵二叉树，其中每个节点， Node.left 的任何后代的值 严格小于 Node.val , Node.right 的任何后代的值 严格大于 Node.val。

二叉树的 前序遍历 首先显示节点的值，然后遍历Node.left，最后遍历Node.right。

示例 1：

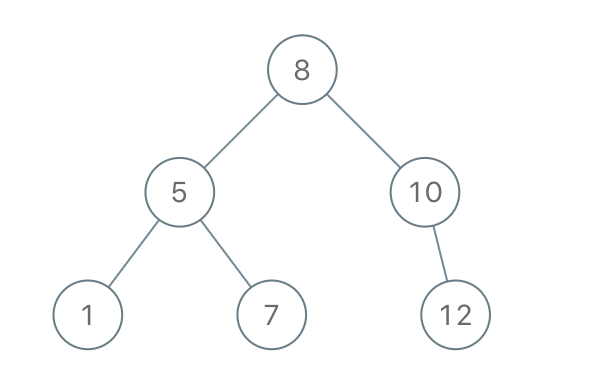
输入：preorder = [8,5,1,7,10,12]

输出：[8,5,10,1,7,null,12]

示例 2:

输入: preorder = [1,3]

输出: [1,null,3]

提示：

• 1 <= preorder.length <= 100

• 1 <= preorder[i] <= 10^8

• preorder 中的值 互不相同

https://leetcode.cn/problems/construct-binary-search-tree-from-preorder-traversal/description/?show=1

思路：

用递归的方式构建，定义 left 与 right ，分别为某个子树在 preorder 中的最左边与最右边的下标。
先建立 根节点 preorder[ left ] ，再去寻找左子树与右子树的交界处。
那么如何寻找左子树与右子树的交界处？
因为是二叉搜索树，所以所有的左子树均小于preorder[ left ] ，所有的右子树 均大于preorder[ left ]

c++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* bstFromPreorder(vector<int>& preorder) {
        return buildSearchTree(preorder,0,preorder.size() - 1);
    }

    TreeNode* buildSearchTree(vector<int>& preorder, int left , int right) {
        if(left>right) {
            return nullptr;
        }
        TreeNode* root = new TreeNode(preorder[left]);
        if(left == right) {
            return root;
        }
        int index = left+1;

        while(index<=right && preorder[index]<preorder[left]) {
            index++;
        }

        root->left = buildSearchTree(preorder,left+1,index-1);
        root->right = buildSearchTree(preorder,index,right);
        return root;
    }

};