数据结构的研究内容

早期，计算机主要用于数值计算:

• 首先，分析问题、提取操作对象，
• 然后，找出操作对象之间的关系，用数学语言加以描述，建立相应数学方程。
• 最后，求解数学方程：高斯消元法、有限元法，差分法……

随着计算机应用领域的扩展，计算机越来越多地用于非数值的计算。

【例1】：学生学籍管理系统

• 操作对象：每位学生的信息（学号、姓名、性别、籍贯、专业等）。
• 操作算法：查询、插入、修改、删除等。
• 操作对象之间的关系：线性关系。
  • 除了开头行和结尾行的操作对象，其余操作对象的行前、后都有其他操作对象，操作对象就像被一根绳子串起来的关系称为线性关系。
• 数据结构：线性数据结构、线性表。

【例2】：人机对弈问题

计算机之所以能和人对弈是因为已经将对弈的策略在计算机汇总存储好。由于对弈的过程是在一定规则之下进行的，所以，为里使计算机能灵活对弈，就必须把对弈过程中所有可能发生的情况及相应的对策都加以考虑。

• 以井字棋为例，初始状态是一个空的棋盘格局。
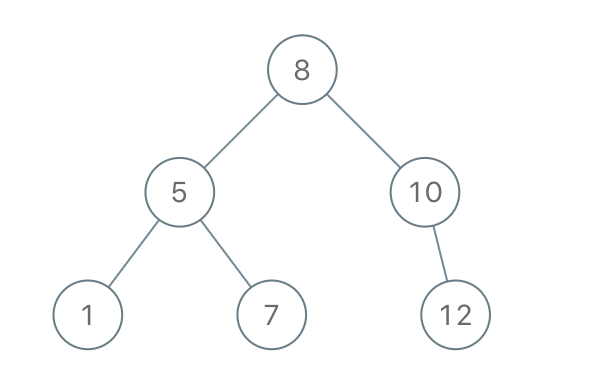
  • 对弈开始后，每下一步棋，则构成一个新的棋盘格局，且对于上一个棋盘格局的可能选择可以有多种形式，因此整个对弈过程就如同下图所示的一棵倒长的树。
  • 在这棵树中，从初始状态（根结点）到某一个最终格局（叶结点）的一条路径，就是一次具体的对弈过程。
• 计算机操作对象：各种棋局状态，即描述棋盘的格局信息。
• 计算机的算法：走棋，即选择一种策略使棋局状态发生变化（由一个格局派生出另一个格局）。
• 操作对象之间的关系：非线性关系、树。

【例3】：最短路径问题

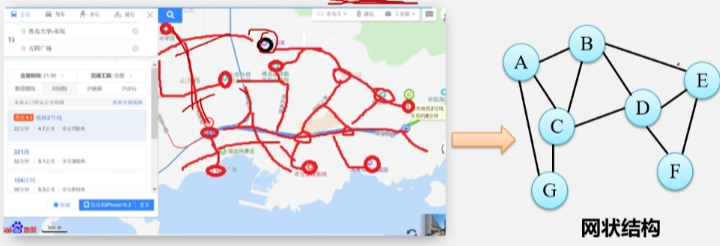
从城市 A 到城市 B 有多条线路，但是每条线路的交通费不同，那么，如何选择一条线路，使得从城市 A 到城市 B 的交通费用最少？

• 解决方法：可以将这类问题抽象为图的最短路径问题。
  • 图中的顶点代表城市，有向边代表两个城市之间的通路，边上的权值代表两个城市之间的交通费。
  • 求解 A 到 B 的最少交通费用，就是要在有向图中 A 点（源点）到达 B 点（终点）的多条路径中，寻找一条各边权值之和最小的路径，即最短路径。

• 操作对象：各地点及路的信息。
• 计算机算法：设置信号灯，求出各个可同时同行的路的集合。
• 对象之间的关系：非线性关系、网状结构。

数据结构研究的内容小结

综上所述

• 这些问题的共同点是无法用数学的公式或程序来描述，而是一些非数值计算的程序设计问题。
• 描述非数值计算问题的数学模型不再是数学方程，而是如：表、树、图之类的具有逻辑关系的数据。
• 数据结构：是一门研究非数值计算的程序设计中计算机的操作对象以及他们之间的关系和操作的学科。