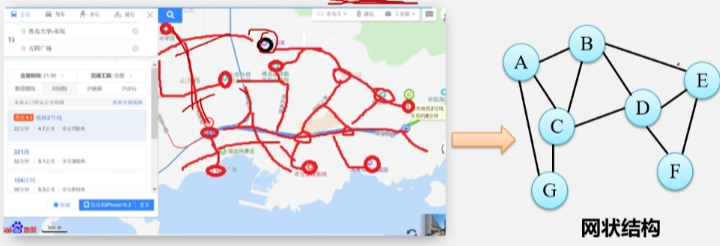
【数据结构】基础：二叉搜索树

news2025/1/10 4:04:56

【数据结构】基础：二叉搜索树

摘要：本文为二叉树的进阶，主要介绍其概念与基本实现（递归与非递归），再介绍其应用，主要介绍内容为KV模型。最后为简单的性能分析。

文章目录

  • 【数据结构】基础：二叉搜索树
    • 一、概念
    • 二、二叉搜索树的实现
    • 三、非递归实现相关操作
      • 3.1 插入
      • 3.2 查找
      • 3.3 删除
    • 四、递归实现相关操作
      • 4.1 插入
      • 4.2 查找
      • 4.3 删除
    • 五、应用
    • 六、性能分析
    • 六、性能分析

一、概念

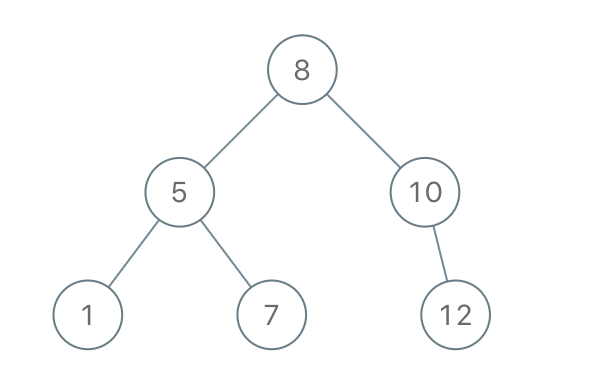
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
  • 它的左右子树也分别为二叉搜索树

二、二叉搜索树的实现

在此使用c++进行最普通的二叉搜索树的实现，首先需要对节点进行定义，节点包括的内容为左右指针以及键值，其次再对该树进行定义，只需要对其根节点进行定义即可，代码示例如下：

template <class K>
class BinarySearchTreeNode {
public:
	BinarySearchTreeNode<K>* left_;
	BinarySearchTreeNode<K>* right_;
	K key_;
	BinarySearchTreeNode(const K& key)
		:left_(nullptr)
		, right_(nullptr)
		, key_(key)
	{}
};

template <class  K>
class BinarySearchTree {
private:
	BinarySearchTreeNode<K>* root_;
public:
	BinarySearchTree()
		:root_(nullptr)
	{}
};

三、非递归实现相关操作

3.1 插入

与一般的二叉树不同，插入节点时需要保护二叉搜索树的结构，因此对以下情况进行分类讨论：

  • 对于空树，直接构建节点并插入
  • 若不为空树，根据二叉搜索树的特性，寻找合适位置进行插入

代码示例如下：

bool Insert(const K& key) {
    // 对于空树，直接构建节点并插入
    if (root_ == nullptr) { 
        root_ = new BinarySearchTreeNode<K>(key);
        return true;
    }
    // 若不为空树，根据二叉搜索树的特性，寻找合适位置进行插入
    BinarySearchTreeNode<K>* parent = nullptr;
    BinarySearchTreeNode<K>* cur = root_;
    while (cur) {
        if (cur->key_ < key) {
            parent = cur;
            cur = parent->right_;
        }
        else if (cur->key_ > key) {
            parent = cur;
            cur = parent->left_;
        }
        else
            return false;
    }
    cur = new BinarySearchTreeNode<K>(key);
    // 虽然找到位置，但忘记了是插到左边还是右边，重新判断一下
    if (cur->key_ < parent->key_) {
        parent->left_ = cur;
    }
    else {
        parent->right_ = cur;
    }
    return true;
}

3.2 查找

根据二叉搜索树的性质进行查找，当遇到较大的节点找右子树，较小的节点找左子树，相等返回，如果不存在则返回空节点

bool Find(const K& key) {
    BinarySearchTreeNode<K>* cur = root_;
    while (cur) {
        if (cur->key_ == key) {
            return true;
        }
        else if (cur->key_ > key) {
            cur = cur->right_;
        }
        else if (cur->key_ < key) {
            cur = cur->left_;
        }
    }
    return false;
}

3.3 删除

对于二叉搜索树的删除是较为复杂的，当删除叶子节点或只有一个子节点的节点是较为简单的，因为这样不太困难的保持树的性质，然而对于存在两个叶子节点的树删除过程是比较困难的，为此需要对各个情况进行分类讨论，过程如下：

情况一：需要删去的节点cur没有子节点

此时，只需要将父节点parent指向该节点指针指向空指针nullptr即可，也可以理解为指向该节点cur的子节点。

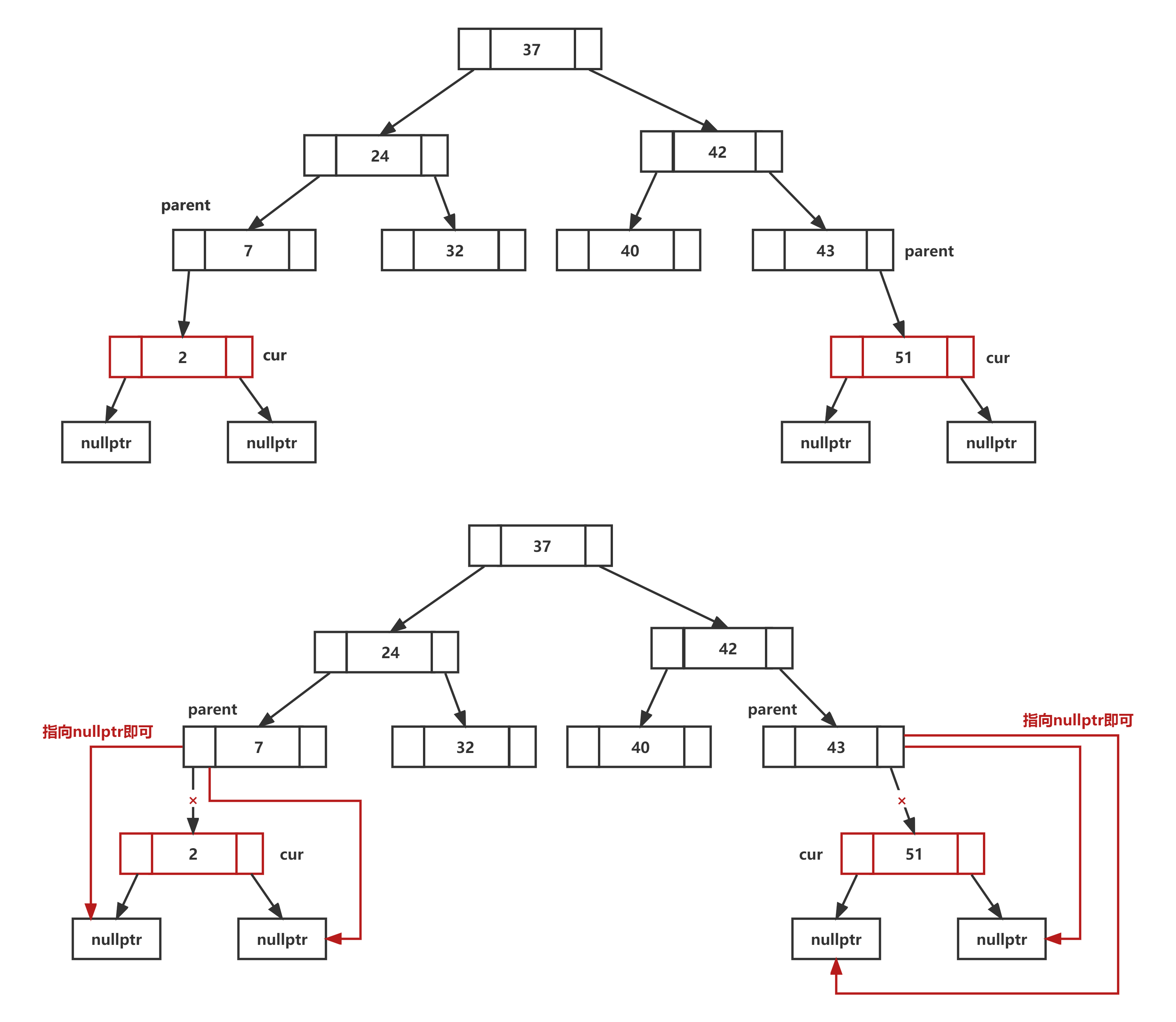
情况二：需要删去的节点cur存在一个子节点

此时需要将父节点parent指向该节点cur指向需要删去的节点cur的非空子节点

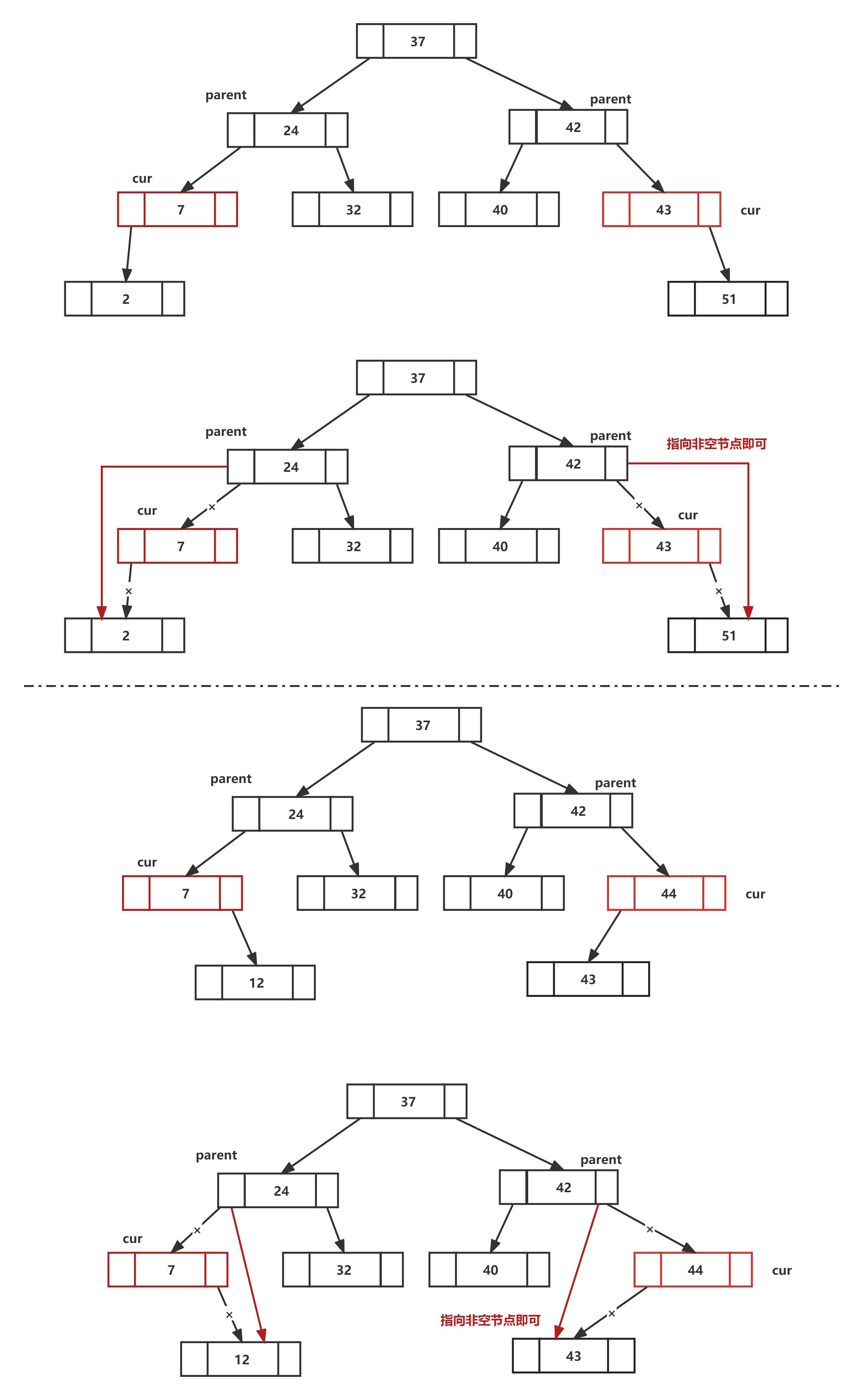
以上两种情况可以将其归类为同一种删除方式，即将父节点指向需要删除节点的子节点，如果子节点非空，则优先指向该节点。

因此可写下如下代码：

// 情况一：不存在子节点
// 情况二：存在一个子节点，该子节点为右节点
if (cur->left_ == nullptr) {
    if (parent->left_ == cur) {
        parent->left_ = cur->right_;
    }
    else {
        parent->right_ = cur->right_;
    }
}
// 情况二：存在一个子节点，该子节点为左节点
else if (cur->right_ == nullptr){
    if (parent->left_ == cur) {
        parent->left_ = cur->left_;
    }
    else {
        parent->right_ = cur->left_;
    }
}

但是，同时需要考虑到如果需要删除的节点是根节点的情况，此时的parent是一个空节点，此特殊情况直接对根节点进行设置即可，代码修改如下：

// 情况一：不存在子节点
// 情况二：存在一个子节点，该子节点为右节点
if (cur->left_ == nullptr) {
    // 删除的为根节点
    if (parent == nullptr) {
        root_ = cur->right_;
    }
    else {
        if (parent->left_ == cur) {
            parent->left_ = cur->right_;
        }
        else {
            parent->right_ = cur->right_;
        }
    }
    delete cur;
}
// 情况二：存在一个子节点，该子节点为左节点
else if (cur->right_ == nullptr){
    // 删除的为根节点
    if (parent == nullptr) {
        root_ = cur->left_;
    }
    else {
        if (parent->left_ == cur) {
            parent->left_ = cur->left_;
        }
        else {
            parent->right_ = cur->left_;
        }
    }
    delete cur;
}

情况三：存在两个子节点，此时采用替代法。所谓替代法就是在子树中寻找一个适合的节点进行替换，一般为左子树的最大节点或右子树的最小节点。此处以右子树的最小节点进行举例，对于右子树的最小节点无疑有两种情况，分别为不存在子节点或者只存在右节点，因为不符合以上两种状态就是不是右子树最小节点。

方法为：

  • 从需要删除的右子树开始找最小子节点，由于二叉搜索树的特性，比较小的节点只能在右节点，如果右节点不存在则没有比其更小的节点，此处使用递归完成寻找
  • 由于进行替换后，还需要保持二叉树的连接，需要引入最小节点的父节点，该父节点需要赋值为需要删除的节点，如果赋值为空的话，可能会因为最小节点是右子树的根，此时父节点仍然是空，会导致程序崩溃
  • 在找到最小节点后，进行替换，覆盖和交换都无所谓，删除方法，因为与值无关
  • 在删除前，需要连接好二叉树，将父节点原本指向最小节点的指针指向最小节点的子节点，非空节点优先，而且只有是右节点有可能，因此直接指向右节点即可

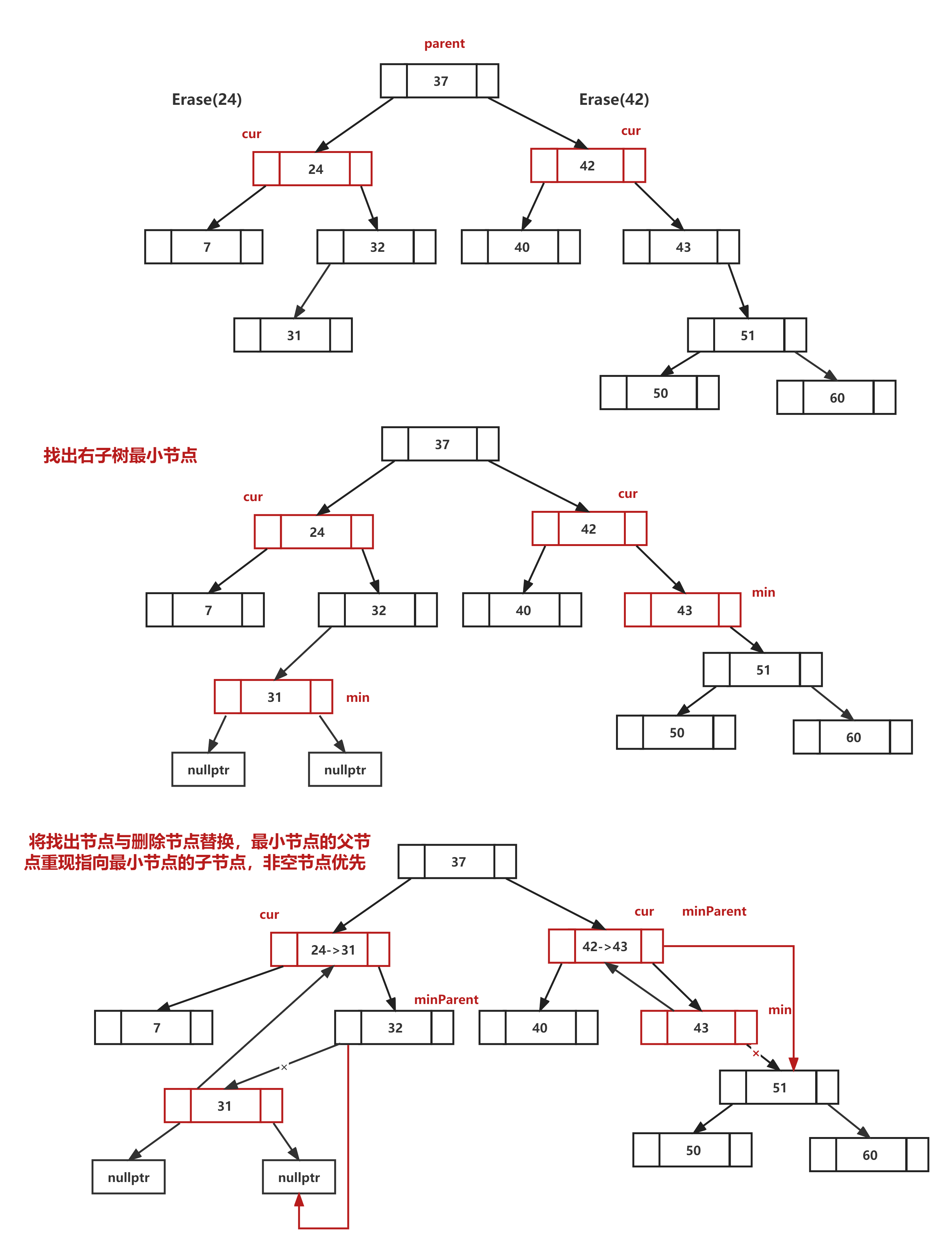
// 情况三：存在两个子节点
else {
    // 从需要删除的右子树开始找最小子节点
    BinarySearchTreeNode<K>* min = cur->right_;
    // 对应的父节点
    BinarySearchTreeNode<K>* minParent = cur;
    // 找最小节点
    while (min->left_) {
        minParent = min;
        min = min->left_;
    }
    // 替换：覆盖法
    cur->key_ = min->key_;
    // 将父节点原本指向最小节点的指针指向最小节点的子节点，非空节点优先(只有右节点有可能）
    if (minParent->left_ == min) {
        minParent->left_ = min->right_;
    }
    else {
        minParent->right_ = min->right_;
    }
    delete min;
}

完整代码如下：

bool Erase(const K& key) {
    BinarySearchTreeNode<K>* parent = nullptr;
    BinarySearchTreeNode<K>* cur = root_;

    while(cur) {
        if (cur->key_ > key) {
            parent = cur;
            cur = cur->left_;
        }
        else if (cur->key_ < key) {
            parent = cur;
            cur = cur->right_;
        }
        else {
            // 情况一：不存在子节点
            // 情况二：存在一个子节点，该子节点为右节点
            if (cur->left_ == nullptr) {
                // 删除的为根节点
                if (parent == nullptr) {
                    root_ = cur->right_;
                }
                else {
                    if (parent->left_ == cur) {
                        parent->left_ = cur->right_;
                    }
                    else {
                        parent->right_ = cur->right_;
                    }
                }
                delete cur;
            }
            // 情况二：存在一个子节点，该子节点为左节点
            else if (cur->right_ == nullptr){
                // 删除的为根节点
                if (parent == nullptr) {
                    root_ = cur->left_;
                }
                else {
                    if (parent->left_ == cur) {
                        parent->left_ = cur->left_;
                    }
                    else {
                        parent->right_ = cur->left_;
                    }
                }
                delete cur;
            }
            // 情况三：存在两个子节点
            else {
                // 从需要删除的右子树开始找最小子节点
                BinarySearchTreeNode<K>* min = cur->right_;
                // 对应的父节点
                BinarySearchTreeNode<K>* minParent = cur;
                // 找最小节点
                while (min->left_) {
                    minParent = min;
                    min = min->left_;
                }
                // 替换：覆盖法
                cur->key_ = min->key_;
                // 将父节点原本指向最小节点的指针指向最小节点的子节点，非空节点优先(只有右节点有可能）
                if (minParent->left_ == min) {
                    minParent->left_ = min->right_;
                }
                else {
                    minParent->right_ = min->right_;
                }
                delete min;
            }
            return true;
        }
    }
    return false;
}

四、递归实现相关操作

4.1 插入

使用递归实现，我们可以将插入转换为子问题，如果空树，将会直接插入，如果不是空树且不存在与树中，将转换为插入到子树的子问题中，进行递归调用。需要注意的是这里的传参，可以使用引用或双指针，否则这里的递归传参是无效的传参。

由于这里设计的树的根节点是私有成员，因此对该递归函数进行了封装，代码示例如下：

public:
	bool Insert_Recursion(const K& key) {
		return _Insert_Recursion(root_, key);
	}
private:
	bool _Insert_Recursion(BinarySearchTreeNode<K>*& root, const K& key) {
		if (root == nullptr) {
			root = new BinarySearchTreeNode<K>(key);
			return true;
		}
		if (key > root->key_) {
			return _Insert_Recursion(root->right_, key);
		}
		else if (key < root->key_) {
			return _Insert_Recursion(root->left_, key);
		}
		else
			return false;
	}

4.2 查找

查找问题同样可以将其转换为子问题，但查找的树是空树或者找到了对应的节点时结束递归，否则根据大小转换为子树查找的子问题。代码示例如下：

public:
	BinarySearchTreeNode<K>* Find_Recurison(const K& key) {
		return _Find_Recurison(root_, key);
	}
private:
	BinarySearchTreeNode<K>* _Find_Recurison(BinarySearchTreeNode<K>* root, const K& key) {
		if (root == nullptr) {
			return nullptr;
		}
		else if (key == root->key_) {
			return root;
		}
		else if (key < root->key_) {
			return _Find_Recurison(root->left_, key);
		}
		else {
			return _Find_Recurison(root->right_, key);
		}
	}

4.3 删除

同样的思路将删除转换为子问题进行解决：

根据二叉树的性质将删除问题转换为子树进行删除的问题，结束条件为删除成功或者是该点不存在，当该点存在时，进行删除，判断其节点个数：

  • 若无节点或者只有一个节点，将父节点与子节点连接，优先非空子节点（由于是引用传递，因此传入的是父节点的别名，直接赋值即可）。
  • 如果存在两个节点，找出合适节点替换，如右子树最小节点，再进行递归删除该节点的右子树。

注意：非递归在书写时是不可以递归调用非递归删除函数的，因为非递归删除是从根节点开始删除，因此对于以根节点的二叉树来说，是不符合二叉搜索树的性质的。

public:
	bool Erase_Recursion(const K& key) {
		return _Erase_Recursion(root_, key);
	}
private:
	bool _Erase_Recursion(BinarySearchTreeNode<K>*& root, const K& key) {
		if (root == nullptr) {
			return false;
		}
		if (root->key_ < key) {
			_Erase_Recursion(root->right_, key);
		}
		else if(root->key_ > key) {
			_Erase_Recursion(root->left_, key);
		}
		else {
			BinarySearchTreeNode<K>* del = root;
			if (root->left_ == nullptr) {
				root = root->right_;
			}
			else if (root->right_ == nullptr) {
				root = root->left_;
			}
			else {
				BinarySearchTreeNode<K>* min = root->right_;
				while (min->left_)
				{
					min = min->left_;
				}
				std::swap(min->key_, root->key_);
				return _Erase_Recursion(root->right_, key);
			}
			delete del;
			return true;
		}
    }

五、应用

二叉搜索树的一般应用为：

  • 搜索功能：Key搜索模型、Key/Value搜索模型
  • 排序与去重功能

此处重点介绍Key搜索模型与Key/Value搜索模型

  • K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值
  • KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。

在之前实现的是K模型的，树的节点只有Key作为关键码储存，而对于KV模型，则需要用键值对进行储存。实际上可以简单的理解为一种检索，因此只需要对K模型进行简单的修改就可以完成KV模型的实现，主要步骤如下：

  • 引入新的成员Value，类型为由模板进行设定

  • 对相应的构造函数、插入函数进行修改，由于这些是与value相关的值

代码示例如下：

namespace ns_KeyValue {
	template <class K,class V>
	class BinarySearchTreeNode {
	public:
		BinarySearchTreeNode<K,V>* left_;
		BinarySearchTreeNode<K,V>* right_;
		K key_;
		V value_;
		BinarySearchTreeNode(const K& key,const V& value)
			:left_(nullptr)
			, right_(nullptr)
			, key_(key)
			, value_(value)
		{}
	};

	template <class  K,class V>
	class BinarySearchTree {
		typedef BinarySearchTreeNode<K, V> BinarySearchTreeNode;
	private:
		BinarySearchTreeNode* root_;
	private:
		void _InOrder(BinarySearchTreeNode* root)
		{
			if (root == nullptr)
			{
				return;
			}

			_InOrder(root->left_);
			cout << root->key_ << ":" << root->value_ << endl;
			_InOrder(root->right_);
		}
	public:
		BinarySearchTree()
			:root_(nullptr)
		{}
		BinarySearchTreeNode* Find(const K& key){
			BinarySearchTreeNode* cur = root_;
			while (cur){
				if (cur->key_ < key){
					cur = cur->right_;
				}
				else if (cur->key_ > key){
					cur = cur->left_;
				}
				else{
					return cur;
				}
			}
			return nullptr;
		}

		bool Insert(const K& key,const V& value) {
			if (root_ == nullptr) {
				root_ = new BinarySearchTreeNode(key,value);
				return true;
			}
			BinarySearchTreeNode* parent = nullptr;
			BinarySearchTreeNode* cur = root_;
			while (cur) {
				if (cur->key_ < key) {
					parent = cur;
					cur = parent->right_;
				}
				else if (cur->key_ > key) {
					parent = cur;
					cur = parent->left_;
				}
				else
					return false;
			}
			cur = new BinarySearchTreeNode(key,value);
			if (cur->key_ < parent->key_) {
				parent->left_ = cur;
			}
			else {
				parent->right_ = cur;
			}
			return true;
		}

		
		bool Erase(const K& key) {
			BinarySearchTreeNode* parent = nullptr;
			BinarySearchTreeNode* cur = root_;

			while (cur) {
				if (cur->key_ > key) {
					parent = cur;
					cur = cur->left_;
				}
				else if (cur->key_ < key) {
					parent = cur;
					cur = cur->right_;
				}
				else {
					// 情况一：不存在子节点
					// 情况二：存在一个子节点，该子节点为右节点
					if (cur->left_ == nullptr) {
						// 删除的为根节点
						if (parent == nullptr) {
							root_ = cur->right_;
						}
						else {
							if (parent->left_ == cur) {
								parent->left_ = cur->right_;
							}
							else {
								parent->right_ = cur->right_;
							}
						}
						delete cur;
					}
					// 情况二：存在一个子节点，该子节点为左节点
					else if (cur->right_ == nullptr) {
						// 删除的为根节点
						if (parent == nullptr) {
							root_ = cur->left_;
						}
						else {
							if (parent->left_ == cur) {
								parent->left_ = cur->left_;
							}
							else {
								parent->right_ = cur->left_;
							}
						}
						delete cur;
					}
					// 情况三：存在两个子节点
					else {
						// 从需要删除的右子树开始找最小子节点
						BinarySearchTreeNode* min = cur->right_;
						// 对应的父节点
						BinarySearchTreeNode* minParent = cur;
						// 找最小节点
						while (min->left_) {
							minParent = min;
							min = min->left_;
						}
						// 替换：覆盖法
						cur->key_ = min->key_;
						// 将父节点原本指向最小节点的指针指向最小节点的子节点，非空节点优先(只有右节点有可能）
						if (minParent->left_ == min) {
							minParent->left_ = min->right_;
						}
						else {
							minParent->right_ = min->right_;
						}
						delete min;
					}
					return true;
				}
			}
			return false;
		}

		void InOrder()
		{
			_InOrder(root_);
			cout << endl;
		}

	};
}

KV模型实例：英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对，在此使用KV模型进行查找与使用，并打印对应的提示信息，代码示例如下：

void Test_Chinese_English() {
	BinarySearchTree<string, string> CE_KVTree;
	CE_KVTree.Insert("left", "左");
	CE_KVTree.Insert("right", "右");
	CE_KVTree.Insert("up", "上");
	CE_KVTree.Insert("down", "下");

	CE_KVTree.InOrder();
	string word;
	while (cin>>word )
	{
		BinarySearchTreeNode<string,string>* ret = CE_KVTree.Find(word);
		if (ret == nullptr) {
			cout << "Without this word\n";
		}
		else {
			cout << ret->value_ << endl;
		}
	}
}

down:下
left:左
right:右
up:上

down
下
left
左
right
右
up
上
dkfjld
Without this word

六、性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：

  • 最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为：log2(N)
  • 最差情况下，二叉搜索树退化为单支树(或者类似单支)，其平均比较次数为：N/2

image-20230130191133551

补充：

  1. 代码将会放到：C++/C/数据结构代码链接 ，欢迎查看！
    E_KVTree.Find(word);
    if (ret == nullptr) {
    cout << “Without this word\n”;
    }
    else {
    cout << ret->value_ << endl;
    }
    }
    }

```shell
down:下
left:左
right:右
up:上

down
下
left
左
right
右
up
上
dkfjld
Without this word

六、性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：

  • 最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为：log2(N)
  • 最差情况下，二叉搜索树退化为单支树(或者类似单支)，其平均比较次数为：N/2

[外链图片转存中…(img-eTDXJ0II-1675151605450)]

补充：

  1. 代码将会放到：C++/C/数据结构代码链接 ，欢迎查看！
  2. 欢迎各位点赞、评论、收藏与关注，大家的支持是我更新的动力，我会继续不断地分享更多的知识！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/189631.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【数据结构】1.1 数据结构的研究内容

【数据结构】1.1 数据结构的研究内容

文章目录数据结构的研究内容数据结构研究的内容小结数据结构的研究内容 早期&#xff0c;计算机主要用于数值计算: 首先&#xff0c;分析问题、提取操作对象&#xff0c;然后&#xff0c;找出操作对象之间的关系&#xff0c;用数学语言加以描述&#xff0c;建立相应数学方程。…
阅读更多...
Java日志门面技术 SLF4J

Java日志门面技术 SLF4J

文章目录背景SLF4J概述切换日志框架实际应用配合自身简单日志实现(slf4j-simple)配置logback日志实现配置Log4J日志实现(需适配器)配置JUL日志实现(需适配器)添加slf4j-nop依赖(日志开关)桥接旧的日志实现框架背景 随着系统开发的进行&#xff0c;可能会更新不同的日志框架&am…
阅读更多...
TF数据流图图与TensorBoard

TF数据流图图与TensorBoard

2.1 TF数据流图 学习目标 目标 说明TensorFlow的数据流图结构应用 无内容预览 2.1.1 案例&#xff1a;TensorFlow实现一个加法运算 1 代码2 TensorFlow结构分析2.1.2 数据流图介绍 2.1.1 案例&#xff1a;TensorFlow实现一个加法运算 2.1.1.1 代码 def tensorflow_demo():&…
阅读更多...
CMMI对企业有什么价值，如何高效落地？

CMMI对企业有什么价值，如何高效落地？

1、获得权威认证 CMMI是全球性软件与系统工程行业的唯一权威认证&#xff0c;是对企业软件研发与能力服务的认可。 CMMI企业价值 CoCode项目管理全面支持CMMI3-5级高效落地​ 2、降本增效&#xff0c;提高企业能力。 CMMI对软件开发过程进行规范化梳理&#xff0c;保证软…
阅读更多...
虚拟机ubuntu系统内存满，无法进入桌面，扩展内存

虚拟机ubuntu系统内存满，无法进入桌面，扩展内存

1、 关闭虚拟机&#xff0c;在虚拟机设置中将原先20GB扩展到30GB 注意&#xff1a;有快照需要删除快照后才能扩展 2、命令行进入ubuntu 内存满了&#xff0c;无法进入Ubuntu图形界面 按下ctrlaltf2~f6组合键 输入用户名和密码进入命令行模式 3、删除一些东西 删除回收站…
阅读更多...
vuex的modules和辅助函数

vuex的modules和辅助函数

一、回顾&#xff1a;vuex状态管理器1、版本问题&#xff1a;vue2对应的是vuex3&#xff1b;vue3对应的vuex42、vuex作用&#xff1a;每个vuex中都有一个Store(仓库)&#xff0c;用于管理vue项目中用到的状态变量&#xff08;属性&#xff09;。vuex维护的是一个单一的状态树vu…
阅读更多...
工作常用cron总结

工作常用cron总结

一、cron表达式详解 corn从左到右&#xff08;用空格隔开&#xff09;&#xff1a; 秒 分 小时 日 月 周 (星期中的日期&#xff0c;1代表周日&#xff0c;7代表周六) 年 定时任务统计 数据同步 0 0 10 * * &#xff1f; 每天上午10点触发…
阅读更多...
Spring 整合Mybatis。

Spring 整合Mybatis。

目录 一、环境准备 1、Mybatis 环境 2、整合思路分析 二、Spring整合Mybatis 三、Spring整合Junit 一、环境准备 1、Mybatis 环境 ▶ 步骤1 : 准备数据库表 Mybatis是来操作数据库表&#xff0c;所以先创建一个数据库及表 create database spring_db character set utf8; …
阅读更多...
LeetCode刷题系列 -- 1008. 前序遍历构造二叉搜索树

LeetCode刷题系列 -- 1008. 前序遍历构造二叉搜索树

给定一个整数数组&#xff0c;它表示BST(即 二叉搜索树 )的 先序遍历 &#xff0c;构造树并返回其根。保证 对于给定的测试用例&#xff0c;总是有可能找到具有给定需求的二叉搜索树。二叉搜索树 是一棵二叉树&#xff0c;其中每个节点&#xff0c; Node.left 的任何后代的值 严…
阅读更多...
JVM的理解（垃圾回收算法和类加载过程）

JVM的理解（垃圾回收算法和类加载过程）

文章目录1、JVM的位置2、JVM的体系结构3、JVM组件3.1、类加载器&#xff08;加载class文件&#xff09;3.1.1、类加载器的执行步骤3.2、PC寄存器3.3、方法区3.4、栈3.5、堆4、GC算法4.1、引用计数法4.2、复制算法1、模型2、原理图4.3、标记清除4.4、标记压缩总结&#xff1a;1、…
阅读更多...
2023年了学Java还能找到工作么？

2023年了学Java还能找到工作么？

Java人才需求缺口巨大 为何还有人找不到工作&#xff1f; 近两年&#xff0c;传统企业开始数字化转型&#xff0c;各企业对互联网IT技术人才呈现井喷趋势。对于进可攻前端、后可守后端的Java程序员而言&#xff0c;市场对他们青睐有加&#xff0c;薪资更是水涨船高。然而在…
阅读更多...
Cesium 本地化部署和新增sandcastle案例

Cesium 本地化部署和新增sandcastle案例

源码下载git clone https://gitee.com/mirrors-gis/cesium.gitcd cesium npm install // or yarn install构建 因为下载的源码，还没有构建出cesium的api，以及api对应的文档 ，如果此时直接运行 npm start ，会启动一个8080端口的一个服务，通过 http://localhost:8080 可以看…
阅读更多...
SpringCloud Alibaba_Nacos服务注册和配置中心

SpringCloud Alibaba_Nacos服务注册和配置中心

目录一、Nacos简介1.为什么叫Nacos2.是什么3.能干嘛4.去哪下5.各种注册中心比较二、安装并运行Nacos三、Nacos作为服务注册中心演示1.官网文档2.基于Nacos的服务提供者3.基于Nacos的服务消费者4.服务注册中心对比4.1 Nacos和CAP4.2 Nacos支持AP和CP模式的切换四、Nacos作为服务…
阅读更多...
sonar的安装以及使用

sonar的安装以及使用

sonar的安装以及使用简介1. sonar是什么2. SonarQube与Sonar安装1.下载sonarqubexxx.zip并且解压即可:2.配置数据库3.重启sonarQube会自动建表。使用1.下载sonar-scanner:(这个工具是对源码进行扫描&#xff0c;并将结果保存到数据库以便用上面的sonarqube进行分析)2.配置mysql…
阅读更多...
Spring Cloud 以及 Spring Cloud Alibaba 使用总结

Spring Cloud 以及 Spring Cloud Alibaba 使用总结

title: Spring Cloud 以及 Spring Cloud Alibaba 使用总结 date: 2023-01-13 11:54:15 tags: Spring categories:Spring cover: https://cover.png feature: false 1. 版本对应 官网版本说明&#xff1a;版本说明 alibaba/spring-cloud-alibaba Wiki (github.com) 这里使用 …
阅读更多...
通过应用场景深度理解监控宝在业务中的实践价值

通过应用场景深度理解监控宝在业务中的实践价值

近年来&#xff0c;越来越多的企业实现了核心业务系统互联网化&#xff0c;无论是企业内部员工还是企业外部用户或是供应链上下游合作伙伴&#xff0c;均通过互联网和Web应用与企业建立起了紧密的联系。基于此&#xff0c;网络性能对企业业务的影响也变得越来越重要&#xff0c…
阅读更多...
阿里云服务器使用docker部署springboot+mysql+redis项目

阿里云服务器使用docker部署springboot+mysql+redis项目

首先&#xff0c;由于springboot中使用的内置的tomcat&#xff0c;需要讲将ttp转为https的自行搜索博客把&#xff1a; 步骤大概是再阿里云上注册免费SSL证书&#xff0c;下载证书后 拖到项目资源目录下&#xff0c;配置application.properties相关属性 下面引出博客主要内容……
阅读更多...
校园网免认证上网的方法

校园网免认证上网的方法

很多时候&#xff0c;当流量不够用时&#xff0c;看着周围那么多热点又连不上&#xff0c;是不是有点心痒痒呢&#xff1f;那么有没有办法不需要要通过这些热点的认证即可上网呢&#xff1f;当然是有的。另外在此强调一点&#xff0c;本教程仅用于学习测试用途&#xff0c;请勿…
阅读更多...
【靶机】vulnhub靶机my_file_server2

【靶机】vulnhub靶机my_file_server2

靶机下载地址&#xff1a;My File Server: 2 ~ VulnHubip&#xff1a;192.168.174.144Kali&#xff1a;192.168.174.128使用arp-scan扫描到ip是使用nmap扫描开放的端口信息&#xff0c;发现靶机开放端口信息如下21端口ftp服务&#xff0c;允许匿名&#xff08;anonymous&#x…
阅读更多...
编译安装nacos集群部署

编译安装nacos集群部署

Nacos 基于 java 开发的&#xff0c;运行依赖于 java 环境。依赖 64 bit JDK 1.8服务器准备&#xff1a;192.168.11.139、192.168.11.141、192.168.11.142 1.首先上传jdk的包 三台都操作tar xzf jdk-8u121-linux-x64.tar.gz -C /usr/local/ 解压jdk的包cd /usr/local/ 切换至解…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023